相关推荐:
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
-----------
LRU 算法就是一种缓存淘汰策略,原理不难,但是面试中写出没有 bug 的算法比较有技巧,需要对数据结构进行层层抽象和拆解,本文 labuladong 就给你写一手漂亮的代码。
计算机的缓存容量有限,如果缓存满了就要删除一些内容,给新内容腾位置。但问题是,删除哪些内容呢?我们肯定希望删掉哪些没什么用的缓存,而把有用的数据继续留在缓存里,方便之后继续使用。那么,什么样的数据,我们判定为「有用的」的数据呢?
LRU 缓存淘汰算法就是一种常用策略。LRU 的全称是 Least Recently Used,也就是说我们认为最近使用过的数据应该是是「有用的」,很久都没用过的数据应该是无用的,内存满了就优先删那些很久没用过的数据。
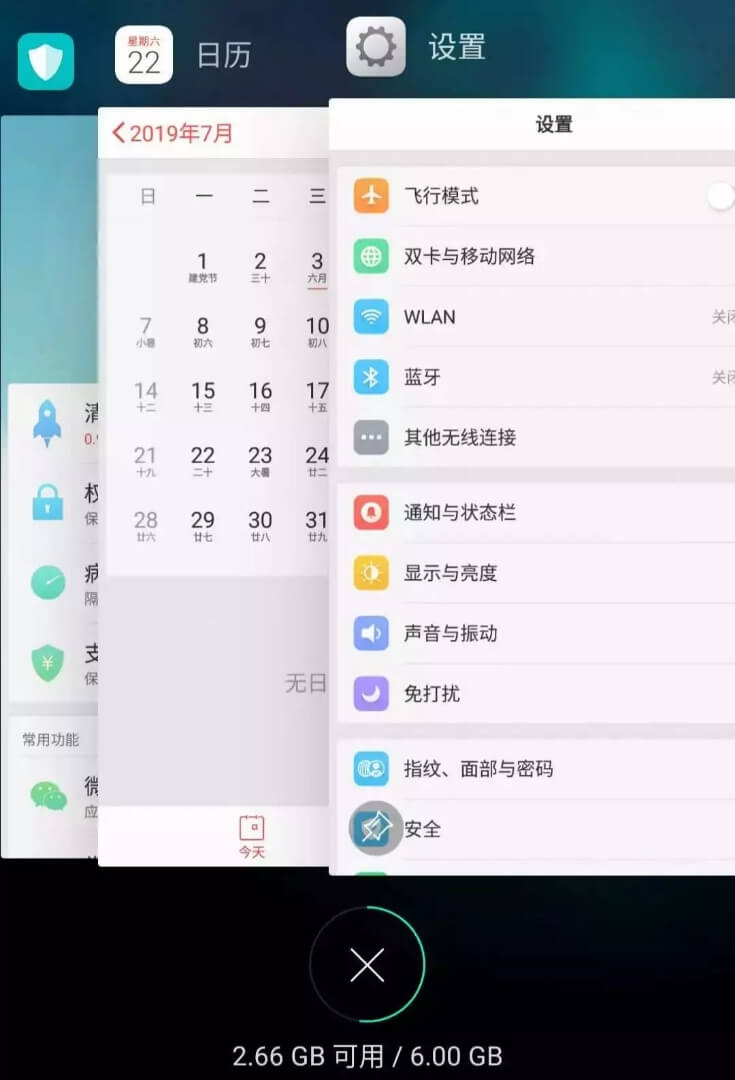
举个简单的例子,安卓手机都可以把软件放到后台运行,比如我先后打开了「设置」「手机管家」「日历」,那么现在他们在后台排列的顺序是这样的:
但是这时候如果我访问了一下「设置」界面,那么「设置」就会被提前到第一个,变成这样:
假设我的手机只允许我同时开 3 个应用程序,现在已经满了。那么如果我新开了一个应用「时钟」,就必须关闭一个应用为「时钟」腾出一个位置,关那个呢?
按照 LRU 的策略,就关最底下的「手机管家」,因为那是最久未使用的,然后把新开的应用放到最上面:
现在你应该理解 LRU(Least Recently Used)策略了。当然还有其他缓存淘汰策略,比如不要按访问的时序来淘汰,而是按访问频率(LFU 策略)来淘汰等等,各有应用场景。本文讲解 LRU 算法策略。
力扣第 146 题「LRU缓存机制」就是让你设计数据结构:
首先要接收一个 capacity 参数作为缓存的最大容量,然后实现两个 API,一个是 put(key, val) 方法存入键值对,另一个是 get(key) 方法获取 key 对应的 val,如果 key 不存在则返回 -1。
注意哦,get 和 put 方法必须都是 O(1) 的时间复杂度,我们举个具体例子来看看 LRU 算法怎么工作。
/* 缓存容量为 2 */
LRUCache cache = new LRUCache(2);
// 你可以把 cache 理解成一个队列
// 假设左边是队头,右边是队尾
// 最近使用的排在队头,久未使用的排在队尾
// 圆括号表示键值对 (key, val)
cache.put(1, 1);
// cache = [(1, 1)]
cache.put(2, 2);
// cache = [(2, 2), (1, 1)]
cache.get(1); // 返回 1
// cache = [(1, 1), (2, 2)]
// 解释:因为最近访问了键 1,所以提前至队头
// 返回键 1 对应的值 1
cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// 解释:缓存容量已满,需要删除内容空出位置
// 优先删除久未使用的数据,也就是队尾的数据
// 然后把新的数据插入队头
cache.get(2); // 返回 -1 (未找到)
// cache = [(3, 3), (1, 1)]
// 解释:cache 中不存在键为 2 的数据
cache.put(1, 4);
// cache = [(1, 4), (3, 3)]
// 解释:键 1 已存在,把原始值 1 覆盖为 4
// 不要忘了也要将键值对提前到队头分析上面的操作过程,要让 put 和 get 方法的时间复杂度为 O(1),我们可以总结出 cache 这个数据结构必要的条件:
1、显然 cache 中的元素必须有时序,以区分最近使用的和久未使用的数据,当容量满了之后要删除最久未使用的那个元素腾位置。
2、我们要在 cache 中快速找某个 key 是否已存在并得到对应的 val;
3、每次访问 cache 中的某个 key,需要将这个元素变为最近使用的,也就是说 cache 要支持在任意位置快速插入和删除元素。
那么,什么数据结构同时符合上述条件呢?哈希表查找快,但是数据无固定顺序;链表有顺序之分,插入删除快,但是查找慢。所以结合一下,形成一种新的数据结构:哈希链表 LinkedHashMap。
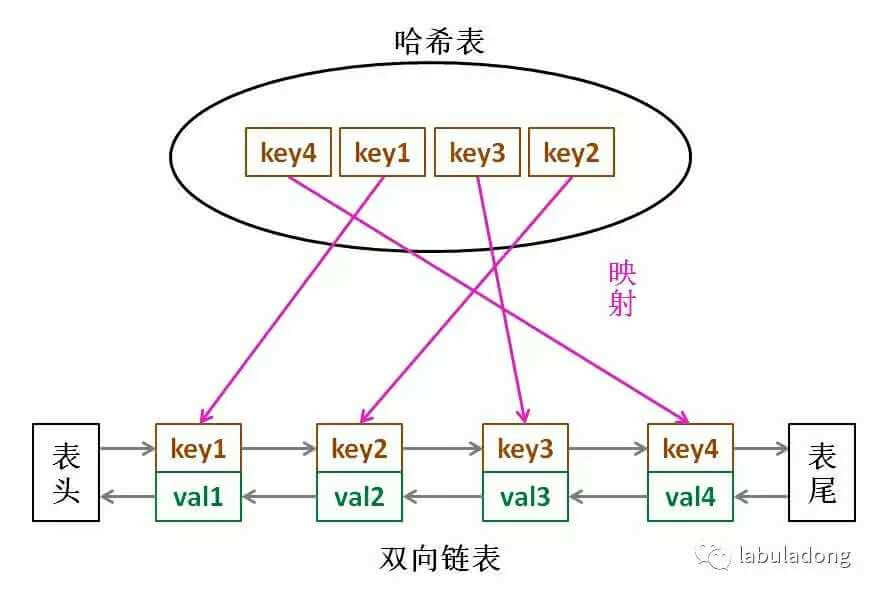
LRU 缓存算法的核心数据结构就是哈希链表,双向链表和哈希表的结合体。这个数据结构长这样:
借助这个结构,我们来逐一分析上面的 3 个条件:
1、如果我们每次默认从链表尾部添加元素,那么显然越靠尾部的元素就是最近使用的,越靠头部的元素就是最久未使用的。
2、对于某一个 key,我们可以通过哈希表快速定位到链表中的节点,从而取得对应 val。
3、链表显然是支持在任意位置快速插入和删除的,改改指针就行。只不过传统的链表无法按照索引快速访问某一个位置的元素,而这里借助哈希表,可以通过 key 快速映射到任意一个链表节点,然后进行插入和删除。
也许读者会问,为什么要是双向链表,单链表行不行?另外,既然哈希表中已经存了 key,为什么链表中还要存 key 和 val 呢,只存 val 不就行了?
想的时候都是问题,只有做的时候才有答案。这样设计的原因,必须等我们亲自实现 LRU 算法之后才能理解,所以我们开始看代码吧~
很多编程语言都有内置的哈希链表或者类似 LRU 功能的库函数,但是为了帮大家理解算法的细节,我们先自己造轮子实现一遍 LRU 算法,然后再使用 Java 内置的 LinkedHashMap 来实现一遍。
首先,我们把双链表的节点类写出来,为了简化,key 和 val 都认为是 int 类型:
class Node {
public int key, val;
public Node next, prev;
public Node(int k, int v) {
this.key = k;
this.val = v;
}
}然后依靠我们的 Node 类型构建一个双链表,实现几个 LRU 算法必须的 API:
class DoubleList {
// 头尾虚节点
private Node head, tail;
// 链表元素数
private int size;
public DoubleList() {
// 初始化双向链表的数据
head = new Node(0, 0);
tail = new Node(0, 0);
head.next = tail;
tail.prev = head;
size = 0;
}
// 在链表尾部添加节点 x,时间 O(1)
public void addLast(Node x) {
x.prev = tail.prev;
x.next = tail;
tail.prev.next = x;
tail.prev = x;
size++;
}
// 删除链表中的 x 节点(x 一定存在)
// 由于是双链表且给的是目标 Node 节点,时间 O(1)
public void remove(Node x) {
x.prev.next = x.next;
x.next.prev = x.prev;
size--;
}
// 删除链表中第一个节点,并返回该节点,时间 O(1)
public Node removeFirst() {
if (head.next == tail)
return null;
Node first = head.next;
remove(first);
return first;
}
// 返回链表长度,时间 O(1)
public int size() { return size; }
}到这里就能回答刚才「为什么必须要用双向链表」的问题了,因为我们需要删除操作。删除一个节点不光要得到该节点本身的指针,也需要操作其前驱节点的指针,而双向链表才能支持直接查找前驱,保证操作的时间复杂度 O(1)。
注意我们实现的双链表 API 只能从尾部插入,也就是说靠尾部的数据是最近使用的,靠头部的数据是最久为使用的。
有了双向链表的实现,我们只需要在 LRU 算法中把它和哈希表结合起来即可,先搭出代码框架:
class LRUCache {
// key -> Node(key, val)
private HashMap<Integer, Node> map;
// Node(k1, v1) <-> Node(k2, v2)...
private DoubleList cache;
// 最大容量
private int cap;
public LRUCache(int capacity) {
this.cap = capacity;
map = new HashMap<>();
cache = new DoubleList();
}先不慌去实现 LRU 算法的 get 和 put 方法。由于我们要同时维护一个双链表 cache 和一个哈希表 map,很容易漏掉一些操作,比如说删除某个 key 时,在 cache 中删除了对应的 Node,但是却忘记在 map 中删除 key。
解决这种问题的有效方法是:在这两种数据结构之上提供一层抽象 API。
说的有点玄幻,实际上很简单,就是尽量让 LRU 的主方法 get 和 put 避免直接操作 map 和 cache 的细节。我们可以先实现下面几个函数:
/* 将某个 key 提升为最近使用的 */
private void makeRecently(int key) {
Node x = map.get(key);
// 先从链表中删除这个节点
cache.remove(x);
// 重新插到队尾
cache.addLast(x);
}
/* 添加最近使用的元素 */
private void addRecently(int key, int val) {
Node x = new Node(key, val);
// 链表尾部就是最近使用的元素
cache.addLast(x);
// 别忘了在 map 中添加 key 的映射
map.put(key, x);
}
/* 删除某一个 key */
private void deleteKey(int key) {
Node x = map.get(key);
// 从链表中删除
cache.remove(x);
// 从 map 中删除
map.remove(key);
}
/* 删除最久未使用的元素 */
private void removeLeastRecently() {
// 链表头部的第一个元素就是最久未使用的
Node deletedNode = cache.removeFirst();
// 同时别忘了从 map 中删除它的 key
int deletedKey = deletedNode.key;
map.remove(deletedKey);
}这里就能回答之前的问答题「为什么要在链表中同时存储 key 和 val,而不是只存储 val」,注意 removeLeastRecently 函数中,我们需要用 deletedNode 得到 deletedKey。
也就是说,当缓存容量已满,我们不仅仅要删除最后一个 Node 节点,还要把 map 中映射到该节点的 key 同时删除,而这个 key 只能由 Node 得到。如果 Node 结构中只存储 val,那么我们就无法得知 key 是什么,就无法删除 map 中的键,造成错误。
上述方法就是简单的操作封装,调用这些函数可以避免直接操作 cache 链表和 map 哈希表,下面我先来实现 LRU 算法的 get 方法:
public int get(int key) {
if (!map.containsKey(key)) {
return -1;
}
// 将该数据提升为最近使用的
makeRecently(key);
return map.get(key).val;
}put 方法稍微复杂一些,我们先来画个图搞清楚它的逻辑:
这样我们可以轻松写出 put 方法的代码:
public void put(int key, int val) {
if (map.containsKey(key)) {
// 删除旧的数据
deleteKey(key);
// 新插入的数据为最近使用的数据
addRecently(key, val);
return;
}
if (cap == cache.size()) {
// 删除最久未使用的元素
removeLeastRecently();
}
// 添加为最近使用的元素
addRecently(key, val);
}至此,你应该已经完全掌握 LRU 算法的原理和实现了,我们最后用 Java 的内置类型 LinkedHashMap 来实现 LRU 算法,逻辑和之前完全一致,我就不过多解释了:
class LRUCache {
int cap;
LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>();
public LRUCache(int capacity) {
this.cap = capacity;
}
public int get(int key) {
if (!cache.containsKey(key)) {
return -1;
}
// 将 key 变为最近使用
makeRecently(key);
return cache.get(key);
}
public void put(int key, int val) {
if (cache.containsKey(key)) {
// 修改 key 的值
cache.put(key, val);
// 将 key 变为最近使用
makeRecently(key);
return;
}
if (cache.size() >= this.cap) {
// 链表头部就是最久未使用的 key
int oldestKey = cache.keySet().iterator().next();
cache.remove(oldestKey);
}
// 将新的 key 添加链表尾部
cache.put(key, val);
}
private void makeRecently(int key) {
int val = cache.get(key);
// 删除 key,重新插入到队尾
cache.remove(key);
cache.put(key, val);
}
}至此,LRU 算法就没有什么神秘的了,敬请期待下文:LFU 算法拆解与实现。
_____________
刷算法,学套路,认准 labuladong,公众号和 在线电子书 持续更新最新文章。
本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode。
======其他语言代码======