Chapter 1: Frequency

In the previous chapter, we made a guess about how the WaveBird worked. Our guess is that it transmits a signal somewhere in the 2.4GHz (2400 MHz) range of radio, when it's on and being given an input, and the specific frequency it uses is derived solely from the channel selector wheel on the bottom.

To test that out, we need a special tool called a spectrum analyzer.

A spectrum analyzer is used to visualize the amount of RF energy present at a given frequency (or range of frequencies). There are several good options out there, including very high-end oscilloscope-sized boxes costing upwards of US$2,000. Personally I prefer to use my trusty HackRF One from Great Scott Gadgets, its bundled ANT500 antenna, and the open-source reciever software Gqrx.

Scanning for the right frequency

This is really pretty easy: Turn on Gqrx, set it to 2400 MHz, press a button on the controller. If you see something show up, you found the right frequency! Otherwise, adjust Gqrx upward by a few MHz and repeat.

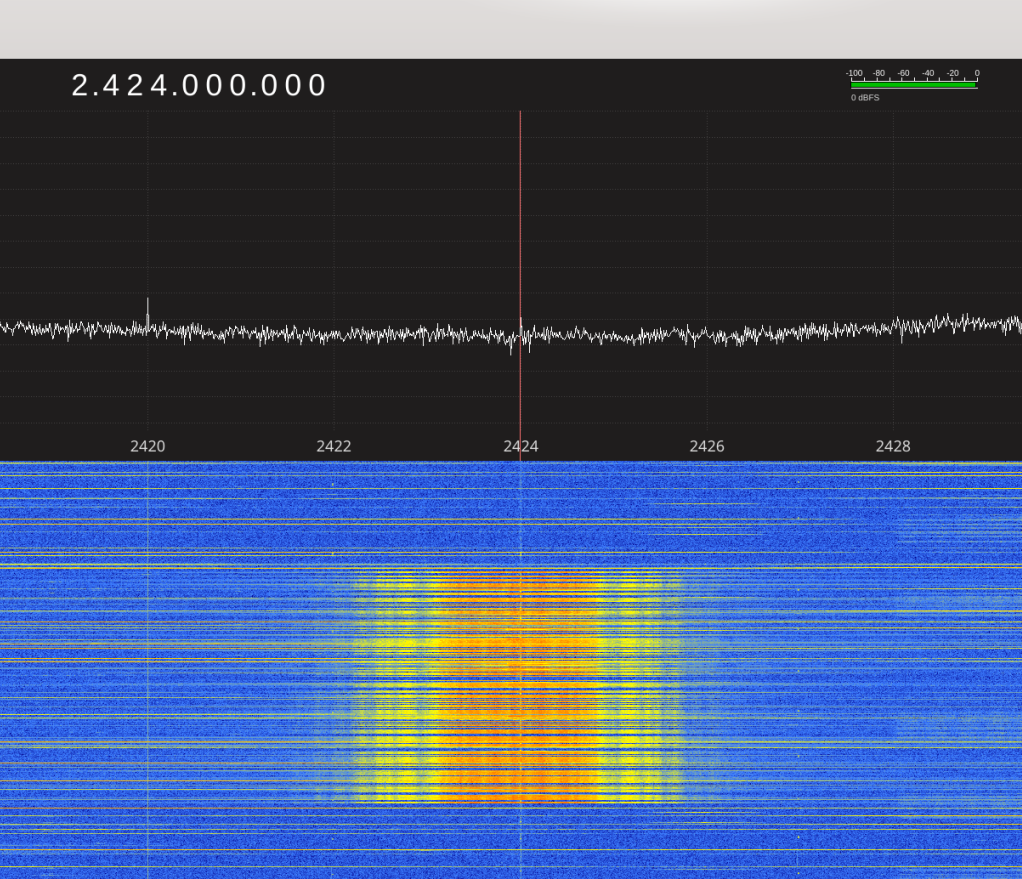
I happened to have my WaveBird set to channel 7 at the time of doing this, and while sweeping through the spectrum, made this fantastic discovery:

Looks like channel 7 corresponds to 2424 MHz! Push button, the signal appears, release button, the signal stops. Great!

The spectrum analyzer does more for us than just identifying the center frequency - we can also use it to measure the signal's "bandwidth" (not to be confused with internet bandwidth) - RF bandwidth is how wide of a slice of spectrum the signal takes up. In this case, the bandwidth appears to be about 2 MHz in either direction, or 4 MHz wide overall.

(As an aside: Pay very close attention to the rippled "fringes" on either side of the signal. Those will be important later.)

All frequencies used by the WaveBird

Repeating this process for each channel, we get the following table:

Channel	Frequency (MHz)
1	2479.2
2	2474.4
3	2404.8
4	2409.6
5	2419.2
6	2414.4
7	2424.0
8	2428.8
9	2438.4
10	2433.6
11	2445.6
12	2450.4
13	2460.0
14	2455.2
15	2464.8
16	2469.6

It's not important to be super precise about the frequency. Thanks to a phenomenon called frequency drift, not even the transmitter will be transmitting on exactly the right frequency. Unless you're a scientific institution with access to really nice atomic clocks (for example, WWV, the time and frequency station operated by the U.S. Government, broadcasts on its standard frequencies with perfect precision), it's virtually guaranteed that imperfections in whatever electronics generate the frequency will be enough to push you at least a few hundred Hz wide of the mark. And even if the transmitter is perfect (like in the case of WWV), your receiver can suffer the same problem.

Radio engineers instead chose to accept that frequency drift is just an unavoidable fact of life and rather focus on developing ways to cope with the problem. Later on we'll see how the WaveBird handles frequency drift and clock skew.

Deriving a frequency from a channel

Of course, we wouldn't be very inquisitive reverse-engineers if we didn't take a swing at how the above table is derived! Let's start by sorting the channels in ascending order of frequency:

3, 4, 6, 5, 7, 8, 10, 9, 11, 12, 14, 13, 15, 16, 2, 1

That's interesting - it looks like 2 and 1 are at the very top (perhaps the physical channel-selection wheel was installed 2 places rotated?) and every other pair of numbers is swapped.

Subtracting 3 (mod 16) from everything puts everything in mostly-sorted order:

0, 1, 3, 2, 4, 5, 7, 6, 8, 9, 11, 10, 12, 13, 15, 14

The second pattern - every odd pair has the odd and even number swapped, can be reordered by XORing the 2s bit of the channel number into the 1s bit:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

There we go! Nice and sorted!

Now let's look at the frequencies themselves, again in ascending order:

2404.8, 2409.6, 2414.4, 2419.2, 2424.0, 2428.8, 2433.6, 2438.4, 2445.6, 2450.4, 2455.2, 2460.0, 2464.8, 2469.6, 2474.4, 2479.2

Looks like each frequency is 4.8 MHz above the last, except for the jump from 2438.4 MHz to 2445.6 MHz, which is 7.2 MHz. That's incidentally also the 8th frequency above the first. So it looks like the first 8 channels are 4.8 MHz apart, the 8th and 9th are 7.2 MHz (1.5 steps), and then everything else continues with the half-separation added in.

So it looks like the algorithm to derive a frequency from a channel is:

1. Take the channel number (1-16) and subtract 3, modulo 16.
2. XOR the 2s bit into the 1s bit.
3. If the number is 8 or above, add half.
4. Multiply by the channel separation of 4.8 MHz, and add the base frequency of 2404.8 MHz

Or, if you prefer it in Python:

def wavebird_freq(chan):
    assert isinstance(chan,int) and 1 <= chan <= 16
    chan -= 3
    chan &= 0xF
    chan ^= bool(chan & 2)
    if chan&8: chan += 0.5
    return chan * 4.8 + 2404.8

What we just did

Well, we found the signal! It's definitely radio, and we also know how the WaveBird derives its center frequency from the channel-selection dial.

Coming up, we'll take a look at how to capture and analyze the radio signal. But first, we need to learn a little bit about radio theory...