This tutorial shows how to implement 1Cycle schedules for learning rate and momentum in PyTorch.
Recent research has demonstrated that the slow convergence problems of large batch size training can be addressed by tuning critical hyperparameters such as learning rate and momentum, during training using cyclic and decay schedules. In DeepSpeed, we have implemented a state-of-the-art schedule called 1-Cycle to help data scientists effectively use larger batch sizes to train their models in PyTorch.
To use 1-cycle schedule for model training, you should satisfy these two requirements:
- Integrate DeepSpeed into your training script using this guide.
- Add the parameters to configure a 1-Cycle schedule to the parameters of your model. We will define the 1-Cycle parameters below.
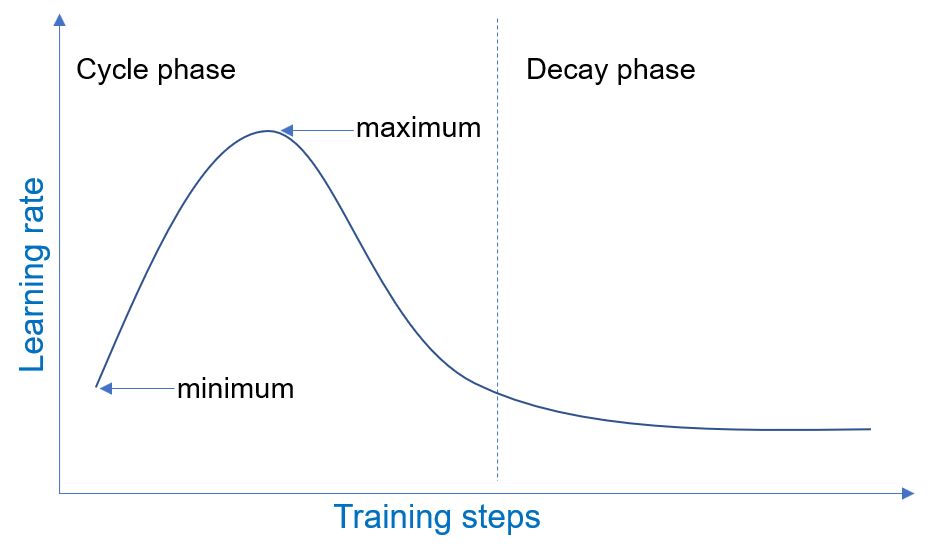
The 1-cycle schedule operates in two phases, a cycle phase and a decay phase, which span one iteration over the training data. For concreteness, we will review how 1-cycle schedule of learning rate works. In the cycle phase, the learning rate oscillates between a minimum value and a maximum value over a number of training steps. In the decay phase, the learning rate decays starting from the minimum value of the cycle phase. An example of 1-cycle learning rate schedule during model training is illustrated below.
The 1-Cycle schedule is defined by a number of parameters which allow users explore different configurations. The literature recommends concurrent tuning of learning rate and momentum because they are correlated hyperparameters. We have leveraged this recommendation to reduce configuration burden by organizing the 1-cycle parameters into two groups to:
- Global parameters for configuring the cycle and decay phase
- Local parameters for configuring learning rate and momentum
The global parameters for configuring the 1-cycle phases are:
cycle_first_step_size: The count of training steps to complete first step of cycle phasecycle_first_stair_count: The count of updates (or stairs) in first step of cycle phasecycle_second_step_size: The count of training steps to complete second step of cycle phasecycle_second_stair_count: The count of updates (or stairs) in the second step of cycle phasepost_cycle_decay_step_size: The interval, in training steps, to decay hyperparameter in decay phase
The local parameters for the hyperparameters are:
Learning rate:
cycle_min_lr: minimum learning rate in cycle phasecycle_max_lr: maximum learning rate in cycle phasedecay_lr_rate: decay rate for learning rate in decay phase
Although appropriate values cycle_min_lr and cycle_max_lr values can be
selected based on experience or expertise, we recommend using learning rate
range test feature of DeepSpeed to configure them.
Momentum
cycle_min_mom: minimum momentum in cycle phasecycle_max_mom: maximum momentum in cycle phasedecay_mom_rate: decay rate for momentum in decay phase
To illustrate the required model configuration changes to use 1-Cycle schedule in model training, we will use a schedule with the following properties:
- A symmetric cycle phase, where each half of the cycle spans the same number of training steps. For this example, it will take 1000 training steps for the learning rate to increase from 0.0001 to 0.0010 (10X scale), and then to decrease back to 0.0001. The momentum will correspondingly cycle between 0.85 and 0.99 in similar number of steps.
- A decay phase, where learning rate decays by 0.001 every 1000 steps, while momentum is not decayed.
Note that these parameters are processed by DeepSpeed as session parameters, and so should be added to the appropriate section of the model configuration.
PyTorch versions 1.0.1 and newer provide a feature for implementing schedulers for hyper-parameters, called learning rate schedulers. We have implemented 1-Cycle schedule using this feature. You will add a scheduler entry of type "OneCycle" as illustrated below.
"scheduler": {
"type": "OneCycle",
"params": {
"cycle_first_step_size": 1000,
"cycle_first_stair_count": 500,
"cycle_second_step_size": 1000,
"cycle_second_stair_count": 500,
"decay_step_size": 1000,
"cycle_min_lr": 0.0001,
"cycle_max_lr": 0.0010,
"decay_lr_rate": 0.001,
"cycle_min_mom": 0.85,
"cycle_max_mom": 0.99,
"decay_mom_rate": 0.0
}
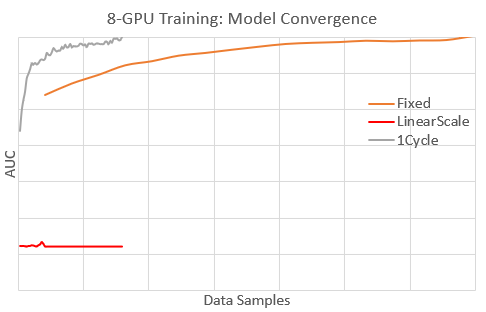
},As example of how 1-Cycle schedule can enable effective batch scaling, we briefly share our experience with an internal model in Microsoft. In this case, the model was well-tuned for fast convergence (in data samples) on a single GPU, but was converging slowly to target performance (AUC) when training on 8 GPUs (8X batch size). The plot below shows model convergence with 8 GPUs for these learning rate schedules:
- Fixed: using an optimal fixed learning rate for 1-GPU training.
- LinearScale: using a fixed learning rate that is 8X of Fixed.
- 1Cycle: using 1-Cycle schedule.
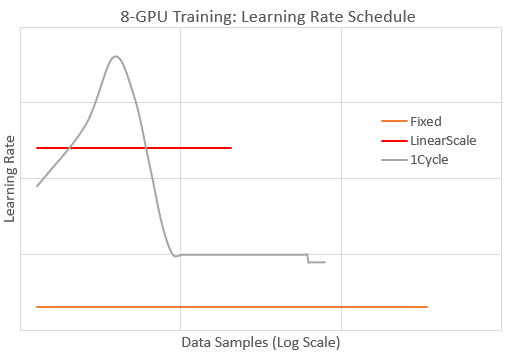
With 1Cycle, the model converges faster than the other schedules to the target AUC . In fact, 1Cycle converges as fast as the optimal 1-GPU training (not shown). For Fixed, convergence is about 5X slower (needs 5X more data samples). With LinearScale, the model diverges because the learning rate is too high. The plot below illustrates the schedules by reporting the learning rate values during 8-GPU training.
We see that the learning rate for 1Cycle is always larger than Fixed and is briefly larger than LinearScale to achieve faster convergence. Also 1Cycle lowers the learning rate later during training to avoid model divergence, in contrast to LinearScale. In summary, by configuring an appropriate 1-Cycle schedule we were able to effective scale the training batch size for this model by 8X without loss of convergence speed.