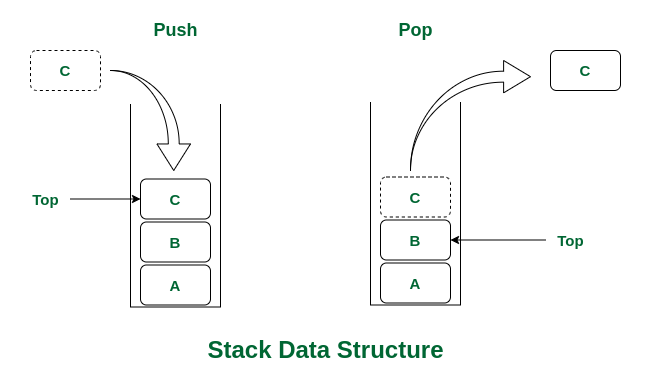
A stack is a linear data structure that follows the Last-In-First-Out (LIFO) principle. This means that the last element added to the stack will be the first one to be removed. Stacks are commonly used in various algorithms and applications such as expression evaluation, backtracking, and managing function calls.
A stack is a collection of elements that supports two main operations:
- Push: Add an element to the top of the stack.
- Pop: Remove an element from the top of the stack.
Stacks are essential data structures used in various computer science applications. They provide a way to manage data in a last-in, first-out manner, which is useful for problems that require reversing or undoing actions.
- Simple Stack: A basic stack where elements are added and removed from the same end (the top).
- Stack with Min/Max: A stack that supports additional operations to get the minimum or maximum element efficiently.
- Stack with Multiple Data Types: A stack that can hold elements of different data types, often implemented using polymorphism.
Common operations performed on stacks include:
- Push: Add an element to the top of the stack.
- Pop: Remove the top element from the stack.
- Peek/Top: Get the element at the top of the stack without removing it.
- IsEmpty: Check if the stack is empty.
In an array-based implementation, a stack uses an array to store its elements. An integer variable, top, is maintained to keep track of the index of the top element of the stack. Elements are added at the position indicated by top and removed from that position.
In a linked list-based implementation, a stack uses a linked list where each node contains data and a reference to the next node. The top pointer keeps track of the top of the stack. The top pointer is used for both pushing and popping elements.
This problem involves checking whether the parentheses in a given expression are balanced. A stack is used to keep track of opening parentheses and ensure that each closing parenthesis matches the most recent unmatched opening parenthesis.
Infix notation is a common way of writing arithmetic expressions (e.g., A + B). However, postfix notation (also known as Reverse Polish Notation) is often used in computer algorithms. This problem involves converting an infix expression to postfix notation using a stack to manage operators and ensure proper order of operations.
Postfix expressions are evaluated using a stack. As the expression is read from left to right, operands are pushed onto the stack, and operators pop operands from the stack, perform the operation, and push the result back onto the stack. The final result is the value remaining on the stack.
- Stack Implementation: Demonstrates how to implement a stack using arrays and linked lists.
- Parenthesis Matching: Checking balanced parentheses in expressions.
- Infix to Postfix Conversion: Converting infix expressions to postfix notation.
- Evaluation of Postfix Expression: Calculating results from postfix expressions.