Basix is a finite element definition and tabulation runtime library. Basix allows users to:
- evaluate finite element basis functions and their derivatives at a set of points;
- access geometric and topological information about reference cells;
- apply push forward and pull back operations to map data between a reference cell and a physical cell;
- permute and transform DOFs to allow higher-order elements to be use on arbitrary meshes; and
- interpolate into and between finite element spaces.
Basix includes a range of built-in elements, and also allows the user to define their own custom elements.
Basix is one of the components of FEniCSx, alongside UFL, FFCx, and DOLFINx.
To install the latest stable version of Basix from pypi.org:
pip install fenics-basixWe currently build binary wheels for Linux and macOS x86-64 architectures.
For advanced and developer installation instructions see the more detailed install instructions
Documentation of Basix can be found at https://docs.fenicsproject.org/basix/main/.
If you find a bug in Basix, you can report it on the GitHub issue tracker.
Questions about using Basix can be asked on the FEniCS discourse group.
Information about how to contribute to Basix can be found here.
In Basix, the sub-entities of the reference interval are numbered as follows:
The following elements are supported on an interval:
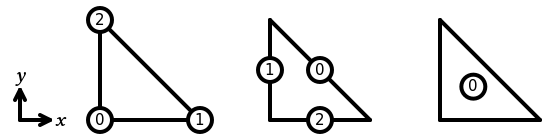
In Basix, the sub-entities of the reference triangle are numbered as follows:
The following elements are supported on a triangle:
- Lagrange
- Nédélec first kind
- Raviart-Thomas
- Nédélec second kind
- Brezzi-Douglas-Marini
- Regge
- Hellan-Herrmann-Johnson
- Crouzeix-Raviart
- Bubble
- Hermite
- iso
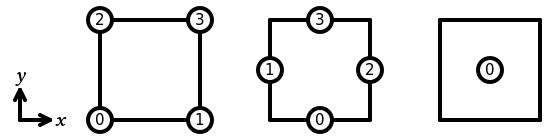
In Basix, the sub-entities of the reference quadrilateral are numbered as follows:
The following elements are supported on a quadrilateral:
- Lagrange
- Nédélec first kind
- Raviart-Thomas
- Nédélec second kind
- Brezzi-Douglas-Marini
- Bubble
- DPC
- Serendipity
- iso
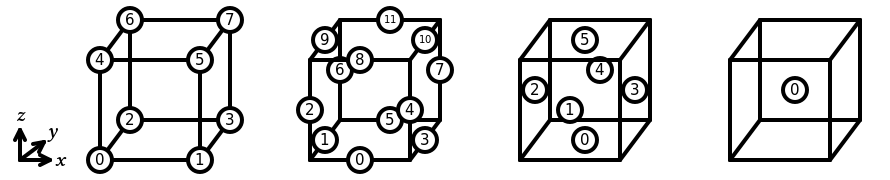
In Basix, the sub-entities of the reference tetrahedron are numbered as follows:
The following elements are supported on a tetrahedron:
- Lagrange
- Nédélec first kind
- Raviart-Thomas
- Nédélec second kind
- Brezzi-Douglas-Marini
- Regge
- Crouzeix-Raviart
- Bubble
- Hermite
- iso
In Basix, the sub-entities of the reference hexahedron are numbered as follows:
The following elements are supported on a hexahedron:
- Lagrange
- Nédélec first kind
- Raviart-Thomas
- Nédélec second kind
- Brezzi-Douglas-Marini
- Bubble
- DPC
- Serendipity
- iso
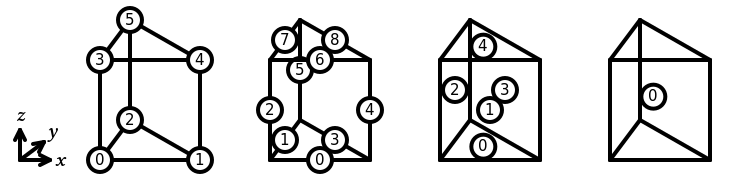
In Basix, the sub-entities of the reference prism are numbered as follows:
The following elements are supported on a prism:
In Basix, the sub-entities of the reference pyramid are numbered as follows:
The following elements are supported on a pyramid: