讲者: Tianqi Chen
过去是通用处理器,通用软件:
AI时代,机器学习编译归根结底就是==部署问题==
什么是机器学习编译
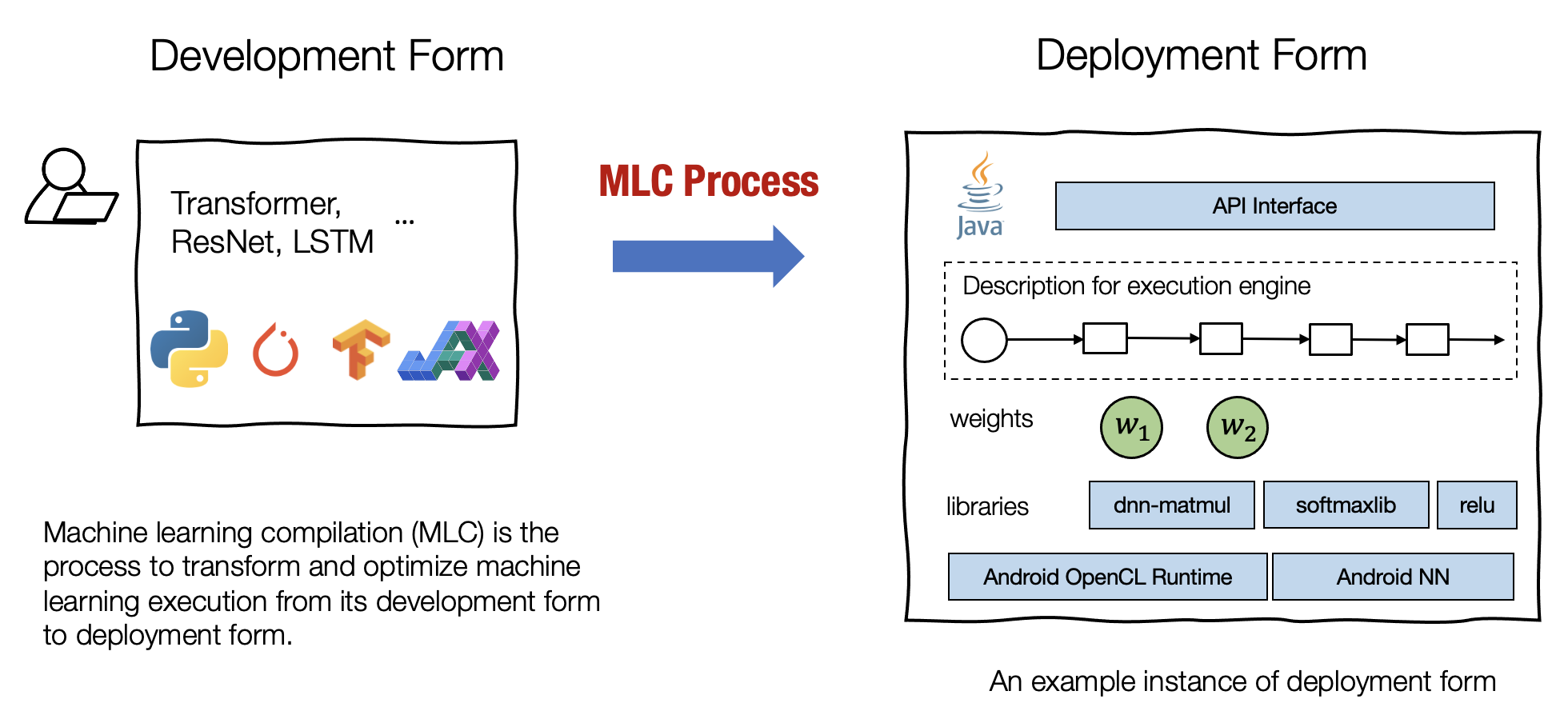
机器学习编译 (machine learning compilation, MLC) 是指,将机器学习算法从开发阶段,通过变换和优化算法,使其变成部署状态。
-
开发形式 是指我们在开发机器学习模型时使用的形式。典型的开发形式包括用 PyTorch、TensorFlow 或 JAX 等通用框架编写的模型描述,以及与之相关的权重。
-
部署形式 是指执行机器学习应用程序所需的形式。它通常涉及机器学习模型的每个步骤的支撑代码、管理资源(例如内存)的控制器,以及与应用程序开发环境的接口(例如用于 android 应用程序的 java API)。
机器学习编译的目标
集成与最小化依赖 部署过程通常涉及集成 (Integration),即将必要的元素组合在一起以用于部署应用程序。 例如,如果我们想启用一个安卓相机应用程序来检测猫,我们将需要图像分类模型的==必要代码==,但不需要模型无关的其他部分(例如,我们不需要包括用于 NLP 应用程序的embedding table)。代码集成、最小化依赖项的能力能够减小应用的大小,并且可以使应用程序部署到的更多的环境。(自己的代码+硬件厂商提供的代码集成)
利用硬件加速 每个部署环境都有自己的一套原生加速技术,并且其中许多是专门为机器学习开发的。机器学习编译的一个目标就是是利用硬件本身的特性进行加速。 我们可以通过构建调用原生加速库的部署代码或生成利用原生指令(如 Nvidia的TensorCore)的代码来做到这一点。
通用优化 有许多等效的方法可以运行相同的模型执行。 MLC 的通用优化形式是不同形式的优化,以最小化内存使用或并行执行提高执行效率的方式转换模型执行。
张量 (Tensor) 是执行中最重要的元素。张量是表示神经网络模型执行的输入、输出和中间结果的多维数组。
张量函数 (Tensor functions) 神经网络的“知识”被编码在权重和接受张量和输出张量的计算序列中。我们将这些计算称为张量函数。值得注意的是,张量函数不需要对应于神经网络计算的单个步骤。部分计算或整个端到端计算也可以看作张量函数。
example:
实际上就是在做==张量函数的变换==
- 右边一般会用一些底层的汇编代码实现!(这里用python写是方便大家看)
- 抽象和实现
我们使用**抽象 (Abstraction)来表示我们用来表示相同张量函数的方式。不同的抽象可能会指定一些细节,而忽略其他实现(Implementations)**细节。例如,linear_relu 可以使用另一个不同的 for 循环来实现。
抽象和实现可能是所有计算机系统中最重要的关键字。抽象指定“做什么”,实现提供“如何”做。没有具体的界限。根据我们的看法,for 循环本身可以被视为一种抽象,因为它可以使用 python 解释器实现或编译为本地汇编代码。
在本章中,我们将讨论对单个单元计算步骤的抽象以及在机器学习编译中对这些抽象的可能的变换。
最底层不可分割的张量函数
我们称这类抽象为 ``张量程序抽象’’。张量程序抽象的一个重要性质是,他们能够被一系列有效的程序变换所改变。
[代码](./Lesson 2-3 notebooks/tensor_program_abstraction_ex.ipynb)
使用张量程序抽象的主要目的是表示循环和相关的硬件加速选择,如多线程、特殊硬件指令的使用和内存访问。机器学习编译核心就是张量程序的变换,这个小节来探讨一下元张量程序变换的示例
为了帮助我们更好地解释,我们用下面的张量计算作为示例。具体地,对于两个大小为
-
$Y_{i, j} = \sum*k A*{i, k} \times B_{k, j}$
-
$C*{i, j} = \mathbb{relu}(Y*{i, j}) = \mathbb{max}(Y_{i, j}, 0)$
上面的计算很像在我们神经网络中经常看到的典型的元张量函数:一个线性层与一个 ReLU 激活层。首先,我们使用如下 NumPy 中的数组计算实现这两个操作。
dtype = "float32"
a_np = np.random.rand(128, 128).astype(dtype)
b_np = np.random.rand(128, 128).astype(dtype)
# a @ b is equivalent to np.matmul(a, b)
c_mm_relu = np.maximum(a_np @ b_np, 0)我们使用python,进行更加底层的实现,给出一些约定:
-
我们将在必要时使用循环计算。
-
如果可能,我们总是通过
numpy.empty显式地分配数组并传递它们。
下面是其中的一种实现方式👇:
def lnumpy_mm_relu(A: np.ndarray, B: np.ndarray, C: np.ndarray):
Y = np.empty((128, 128), dtype="float32")
for i in range(128):
for j in range(128):
for k in range(128):
if k == 0:
Y[i, j] = 0
Y[i, j] = Y[i, j] + A[i, k] * B[k, j]
for i in range(128):
for j in range(128):
C[i, j] = max(Y[i, j], 0)下面检验一下实现是否等价
c_np = np.empty((128, 128), dtype=dtype)
lnumpy_mm_relu(a_np, b_np, c_np)
np.testing.assert_allclose(c_mm_relu, c_np, rtol=1e-5)在看过低级 NumPy 示例后,现在我们准备介绍 TensorIR。
下面的代码块展示了 mm_relu 的 TensorIR 实现。这里的代码是用一种名为 TVMScript 的语言实现的,它是一种嵌入在 Python AST 中的特定领域方言。
@tvm.script.ir_module
class MyModule:
@T.prim_func
def mm_relu(A: T.Buffer[(128, 128), "float32"],
B: T.Buffer[(128, 128), "float32"],
C: T.Buffer[(128, 128), "float32"]):
T.func_attr({"global_symbol": "mm_relu", "tir.noalias": True})
Y = T.alloc_buffer((128, 128), dtype="float32")
for i, j, k in T.grid(128, 128, 128):
with T.block("Y"):
vi = T.axis.spatial(128, i)
vj = T.axis.spatial(128, j)
vk = T.axis.reduce(128, k)
with T.init():
Y[vi, vj] = T.float32(0)
Y[vi, vj] = Y[vi, vj] + A[vi, vk] * B[vk, vj]
for i, j in T.grid(128, 128):
with T.block("C"):
vi = T.axis.spatial(128, i)
vj = T.axis.spatial(128, j)
C[vi, vj] = T.max(Y[vi, vj], T.float32(0))- T.Buffer: 底层的抽象,保存一些数据(与函数的形参一一对应)
- T.grid将深层的循环♻️对应在一起
实际上语句也是一一对应关系,如下图所示:
- 唯一不同的地方就在于:(这个是tensorIR的特殊构造)
with T.block("Y"):
vi = T.axis.spatial(128, i)
vj = T.axis.spatial(128, j)
vk = T.axis.reduce(128, k)- 块 是 TensorIR 中的基本计算单位。值得注意的是,该块包含比普通 NumPy 代码更多的信息。一个块包含一组块轴(
vi、vj、vk)和围绕它们定义的计算。 vi,vj所在矩阵T的最后维度中,就是spacial axis。并且与位置无关可以先算Y[0, 1]也可以先算Y[5, 2]vk所在矩阵T中维度是消失的,需要在循环里面全部都跑一遍。- 并且绑定的循环迭代器都是0~127的
"tir.noalias": True对应不同的内存指针@T.prim_func表示元张量函数
Y[0, 1] 条件下跑k的循环[0~127]- 上面的三行声明了关于块轴的关键性质,语法如下。
[block_axis] = T.axis.[axis_type]([axis_range], [mapped_value])这三行包含以下信息:
- 定义了
vi、vj、vk应被绑定到的位置(在本例中为i、j和k); - 声明了
vi、vj、vk的原始范围(T.axis.spatial(128, i)中的128); - 声明了块轴的属性(
spatial,reduce)。
但一般为了简单起见,我们会写成:
vi, vj, vk = T.axis.remap("SSR", [i, j, k])@tvm.script.ir_module
class MyModule:
@T.prim_func
def mm_relu(A: T.Buffer[(128, 128), "float32"],
B: T.Buffer[(128, 128), "float32"],
C: T.Buffer[(128, 128), "float32"]):
T.func_attr({"global_symbol": "mm_relu", "tir.noalias": True})
Y = T.alloc_buffer((128, 128), dtype="float32")
for i, j, k in T.grid(128, 128, 128):
with T.block("Y"):
vi, vj, vk = T.axis.remap("SSR", [i, j, k])
with T.init():
Y[vi, vj] = T.float32(0)
Y[vi, vj] = Y[vi, vj] + A[vi, vk] * B[vk, vj]
for i, j in T.grid(128, 128):
with T.block("C"):
vi = T.axis.spatial(128, i)
vj = T.axis.spatial(128, j)
C[vi, vj] = T.max(Y[vi, vj], T.float32(0))同时,IR Module当中还可以包括多个元张量函数!
[Notebook](./Lesson 2-3 notebooks/tensor_it_ex.ipynb)
[Notebook](./Lesson 4 notebooks/end_to_end_model.ipynb)
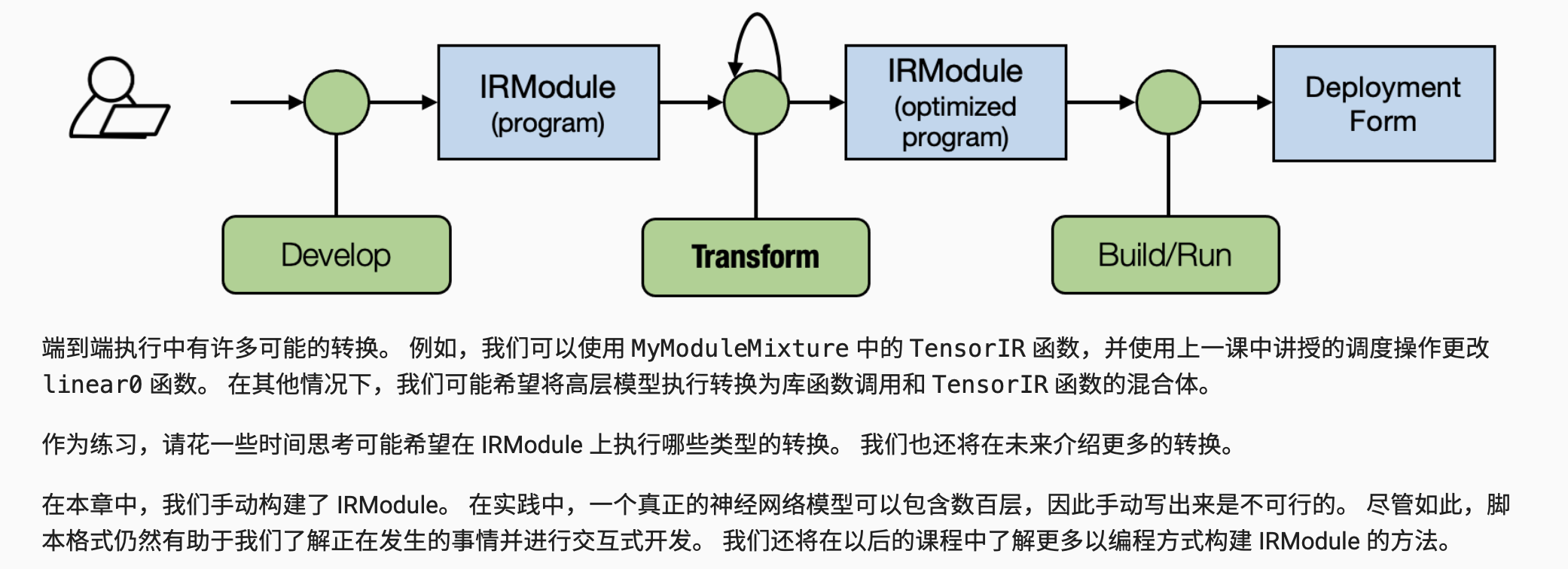
在本章中,我们讨论了许多描述端到端模型执行的方法。 我们可能已经注意到的一件事是我们回到了抽象和实现的主题。
TensorIR函数和库函数都遵循相同的目标传递方式。 因此,我们可以在示例中简单地将调用从一个替换为另一个。- 我们可以使用不同的方式来表示MLC过程不同阶段的计算。
到目前为止,我们已经介绍了一些转换端到端 IRModule 的方法(例如参数绑定)。 让我们回到 MLC 的共同主题:MLC 过程是在不同的抽象表示之间执行并在它们之间进行转换。
- 计算图抽象有助于将元张量函数拼接在一起以进行端到端执行。
- Relax 抽象的关键要素包括
call_tir构造,将目标传递规范的元函数嵌入到计算图中Dataflow block
- 计算图允许调用环境库函数和
TensorIR函数。