SPS - Stochastic Polyak Step-size [paper]
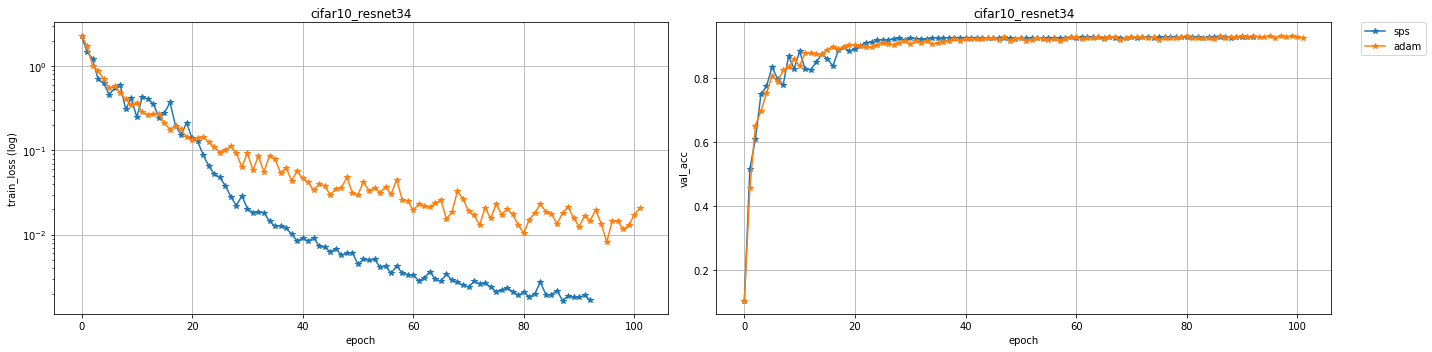
Fast convergence with SPS optimizer. The first efficient stochastic variant of the classical Polyak step-size for SGD
pip install git+https://github.com/IssamLaradji/sps.git
Use Sps in your code by adding the following script.
import sps
opt = sps.Sps(model.parameters())
for epoch in range(100):
# create loss closure
def closure():
loss = torch.nn.MSELoss()(model(X), y)
loss.backward()
return loss
# update parameters
opt.zero_grad()
opt.step(closure=closure)python trainval.py -e mnist -sb ../results -r 1
where -e is the experiment group, -sb is the result directory.
python trainval.py -e kernel -sb ../results -r 1
jupyter nbextension enable --py widgetsnbextension --sys-prefix
jupyter notebook
from haven import haven_jupyter as hj
from haven import haven_results as hr
from haven import haven_utils as hu
# path to where the experiments got saved
savedir_base = '../results'
# filter exps
filterby_list = [{'dataset':'cifar10', 'opt':{'c':0.2}},
{'dataset':'cifar10', 'opt':{'name':'adam'}}]
# get experiments
rm = hr.ResultManager(savedir_base=savedir_base,
filterby_list=filterby_list,
verbose=0)
# dashboard variables
legend_list = ['opt.name']
title_list = ['dataset', 'model']
y_metrics = ['train_loss', 'val_acc']
# launch dashboard
hj.get_dashboard(rm, vars(), wide_display=True)@article{loizou2020stochastic,
title={Stochastic polyak step-size for SGD: An adaptive learning rate for fast convergence},
author={Loizou, Nicolas and Vaswani, Sharan and Laradji, Issam and Lacoste-Julien, Simon},
journal={arXiv preprint arXiv:2002.10542},
year={2020}
}
It is a collaborative work between labs at MILA, Element AI, and UBC.
- Thank you Less Wright for incorporating the gradient centralization method, it seems to improve the results in some experiments.