This is a summer intern project in Advanced Computer Architecture Lab, SJTU. SGEMM means floating point matrix multiplication. I implemented matrix multiplication on CUDA-8.0 based on five different method. Some of the methods archieved almost the same performance as cuBLAS.
Name: GeForce GTX 1080 Ti
Compute capability: 6.1
All the methods are based on the basic multiplication method, whose time complexity is O(N3). So the optimization focused on low level method, such as reduce the accession in global memory and the number of instructions.
The key idea for CUDA programming is properly assigning work to each threads. Then consider the grid size and block size according to specific matrix size. The main difficulty is to correctly index each value.
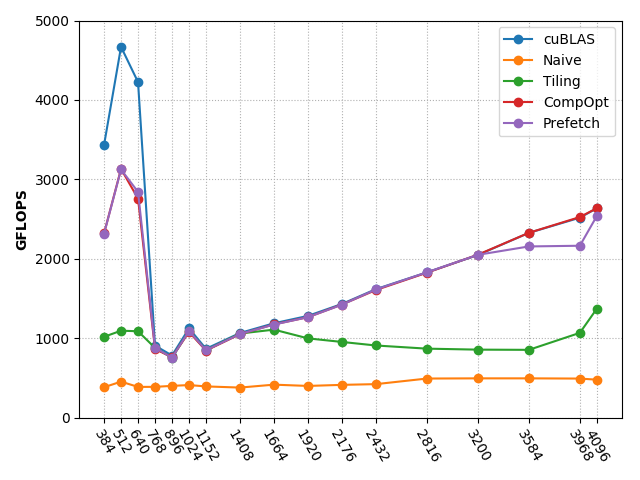
We use GFLOPS to measure the performance of different methods. In computing, floating point operations per second(FLOPS) is a measure of computer performance. It is also commonly used in researches about matrix multiplication on GPU.
Consider matrix multiplication: A(MxK) x B(KxN) = C(MxN). If the time spent on computing is t, the GFLOPS is:
2xMxKxN / t / 1e9
In the experiment, I evaluate GFLOPS with different size of matrix.
The perforamce of cuBLAS is as follows:

Each thread calculates one value of output matrix C. This is quite simple and straight forward. Performance:

Each thread loads one value of TxT submatrix of A and B and calculate one value of submatrix of C. We need to iterate K / T times to accumulate the value of submatrix of C.

CompOpt is Computational Optimization. The current architecture of Stream Multiprocessor(SM) only allows one source operand from the shared memory. However, computing the inner product requires two source operands from the shared memory. One solution is to perform outer product instead of inner product.
In this method, matrix A is stored in shared memory with TILE size of TxT, but matrix B and C are stored in registers. Each thread needs to load TILE_SIZE / VECTOR_SIZE values of A and a vector of C with size of TILE_SIZE(As(TILE_SIZEx1) x Bv). Here VECTOR_SIZE is another parameters.
Now we can see that the performance is almost the same as cuBLAS.

This method is a further optimization of CompOpt method and is based on the concurrency between load and store instructions. While we do the outer product, we fetch the next tile of matrix A.
The performance is almost the same as the previous method.
Compile the file as follows:
nvcc *.cu --std=c++11
If compile the benchmark code with cuBLAS, compile as follows:
nvcc matmul_cublas.cu --std=c++11 -lcublas
This project was mainly inspired by this tuorial. I refine the code to avoid hard coding.