1. 라플라시안의 정의 (definition)

유클리드 공간에서 두 번 미분할 수 있는 스칼라 함수 $f$에 대하여 라플라시안(laplacian)은 $f$에 대한 그레디언트의 발산으로 정의되며 수식으로 표현하면 다음과 같다.

$$\Delta f = \nabla ^2 f = \nabla \cdot \nabla f$$

수식 상으로는 그렇다고 하긴 하는데... 라플라시안의 직관적인 이해를 해보도록 하자.

2. 스칼라 함수의 기울기(gradient)와 발산(divergence)

라플라시안은 쉽게 말하면 스칼라 함수 에 대해서

$$div(grad(f))$$

와 같이 gradient 연산을 먼저 취해준 뒤, 그것으로 출력되는 벡터장에 대해 divergence를 구한 것이다.

다음과 같은 스칼라 함수를 생각해보자. MATLAB에서 peak라는 함수를 이용해서 만들 수 있는 아주 예쁜 스칼라 함수이다.

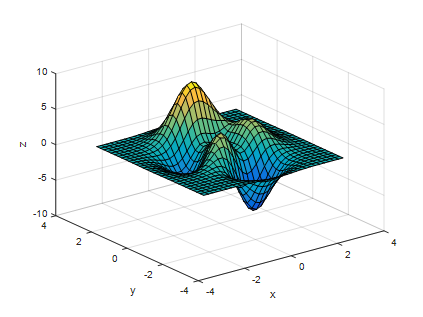
그림 1 MATLAB의 peak 함수를 그린 것. 이것의 gradient는?

그림 1에는 MATLAB의 peak 함수가 표현되어 있다.

이 스칼라 함수에 대해 gradient를 구하면 어떤 결과를 예측할 수 있을까?

gradient는 경사도를 얘기하는데 가파르게 올라가는 방향으로 벡터장이 형성된다.

글로 설명하니 모호하게 들릴 수도 있지만 스스로 어떤 벡터장이 나올지 미리 상상해보도록 하자.

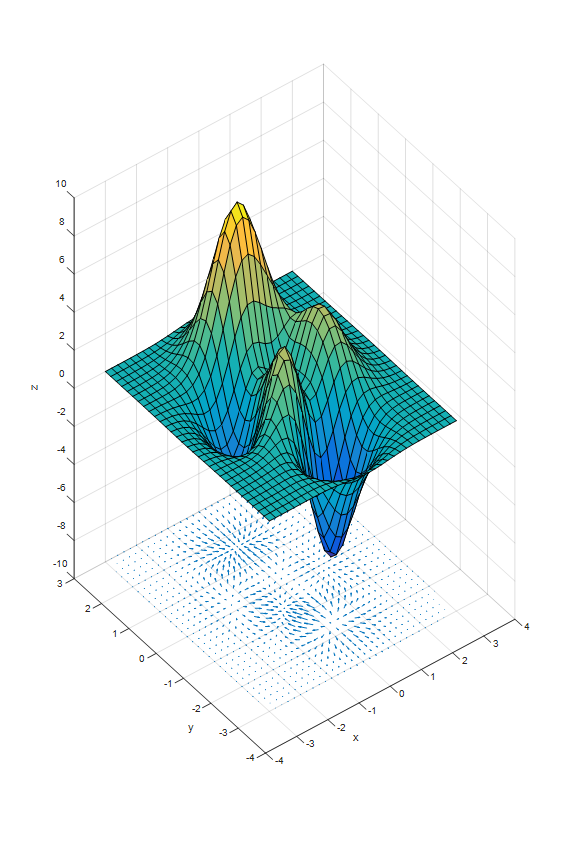
그림 2 peak 함수와 그 gradient가 표시되어 있다.

그림 2의 벡터장의 z 좌표가 –10인 것은 peak 함수와 벡터장을 한번에 표시하기 위해 임의로 정한 것이다.

그림 2를 보면 x, y 좌표의 (0, 2) 부근에는 한 점으로 수렴하는 벡터장이 형성되고 있고, x, y 좌표의 (0,-2) 부근에는 한 점에서 발산하는 벡터장이 형성되어 있다.

이제 이 벡터 장의 divergence를 구하면 어떨까?

(0, 2) 부근에서는 수렴하는 형태이기 때문에 divergence는 음의 값이 될 것이고 (0,-2) 부근에서는 발산하는 형태이기 때문에 divergence는 양의 값이 될 것이다.

즉, 어떤 스칼라 함수의 gradient를 취한 것에 divergence를 취해주면 이 스칼라 함수의 높이 값이 얼마나 낮은 지를 수치로 보여주는 것과 같다.

2차원 평면에 그린 grad($f$)를 통해 정말 그 말이 맞을지 확인해보자.

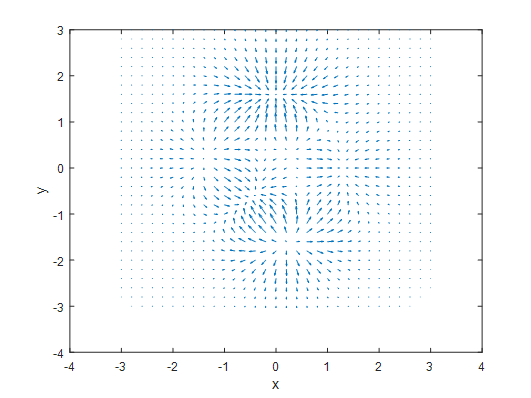
그림 3 peak 함수의 gradient를 xy 평면에 그린 것.

그림 2에 표시한 벡터장을 xy 평면으로 옮긴 것이 그림 3이다. 이제 여기에 divergence를 구해서 색깔로 표시해보자.

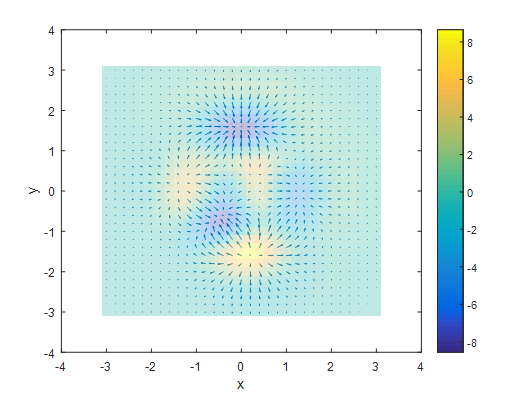
그림 4 그림 3의 벡터장에 divergence를 적용하여 색깔로 표시한 것

방금 필자가 말하기를 divergence는 스칼라 함수의 높이가 얼마나 낮은지를 알려준다고 했기 때문에 divergence의 역수는 높이가 얼마나 높은지를 알려주는 값이 된다.

그림 5와 6을 보면 정말로 divergence의 음의 값이 peak 함수의 높이와 정말 비슷하다는 것을 알 수 있다.

실제로는 laplacian은 2차 편미분의 값을 말해준다. 즉, laplacian은 스칼라 함수가 해당 포인트에서 아래로 볼록한지 ($\nabla^2f>0$) 또는 위로 볼록한지($\nabla^2f<0$)를 말해주는 것이다.

이것은 고등학교 때 배운 2차 미분 계수의 의미와 동일한 것이다.