/*******************************************************************
Cycle Detection
1. How to perform cycle detection in a directed graph
2. How to perform cycle detection in an undirected graph
COMP9024
*******************************************************************/Detecting cycles in a graph is a fundamental problem in computer science and graph theory.
// Test whether a graph contains a cycle.
int HasCycle(struct Graph *pGraph);Depth First Search (DFS) can be used to detect cycles in a graph.
A "back edge" is an edge that connects a node to one of its ancestors in a DFS traversal.
If a back edge is encountered during DFS, it indicates the presence of a cycle.
Given a back edge from node v to node u, it implies that node u is an ancestor of node v in a DFS traversal, and there exists a path (consisting of nodes pushed on the call stack in a recursive DFS traversal) from u to v, thereby forming a cycle as follows.
u -> ... -> v -> uSuppose a DFS traversal starts from the node 0.
In the following directed graph, the edge from node 4 to node 0 is a back edge.
Node 0 is an ancestor of node 4 in the DFS traversal.
When the DFS algorithm arrives at node 4, it checks node 0, one of the adjacent nodes of node 4:
(Node 0 has been visited) && (Node 0 is on the call stack)If we implement the DFS algorithms recursively, the nodes on the call stack are 4, 2, and 0, with node 4 being the top element.
In other words, we have detected a cycle starting from node 0 to node 0 as follows.
0 -> 2 -> 4 -> 0| Visiting 4 |
|---|
| Nodes on call stack: |
 |
- Set a breakpoint at the entry of DetectCycle() (i.e., line 345 in src/Graph.c) when debugging this project in VS Code.
- Observe the parameter u of each stack frame on the call stack
// DetectCycle() is a recursive function
static int DetectCycle(struct Graph *pGraph, long u, int *visited, struct Stack *pNodesOnStack) {
// ...
int cycleDetected = 0;
for(long v = 0; v < pGraph->n; v++) {
if (MatrixElement(pGraph, u, v)) {
if (!visited[v]) {
if (DetectCycle(pGraph, v, visited, pNodesOnStack)) {
// ...
return cycleDetected;
}The DetectCycle() function is implemented recursively for DFS traversal to detect cycles.
As it is hard to access the nodes on the call stack, we create a data stack to record the nodes.
When entering the function DetectCycle(), the current node is pushed onto the data stack.
When DetectCycle() returns, the node is popped from the data stack.
static int DetectCycle(struct Graph *pGraph, long u, int *visited, struct Stack *pNodesOnStack) {
// Entry
StackPush(pNodesOnStack, u);
// ...
// Exit
StackPop(pNodesOnStack);
}Motivation in this project:
Visiting all the current nodes on a data stack, without changing itIn computer programming, an iterator is an object that allows a programmer to traverse through elements of a container.
An iterator provides a way to access elements of a collection, like lists or arrays, one at a time without exposing the underlying structure.
It typically implements methods like next() or NextItem() to retrieve the next element and HasNext() to check if there are more elements to iterate over.
This abstraction makes it easier to work with collections in a uniform way, regardless of their specific implementations.
// src/Stack.h
typedef long STACK_ITEM_T;
// ...
void StackPush(struct Stack *pStack, STACK_ITEM_T item);
STACK_ITEM_T StackPop(struct Stack *pStack);
/*********************** Iterator interface for a stack ******************/
typedef struct {
void *pStackElement;
} StackIterator;
StackIterator GetIterator(struct Stack *pStack);
int HasNext(StackIterator *it);
STACK_ITEM_T NextItem(StackIterator *it);
void TestIterator(void);// src/Stack.c
StackIterator GetIterator(struct Stack *pStack) {
StackIterator iterator;
iterator.pStackElement = pStack->top;
return iterator;
}
int HasNext(StackIterator *pIt) {
StackNode *cur = (StackNode *)(pIt->pStackElement);
return cur != NULL;
}
STACK_ITEM_T NextItem(StackIterator *pIt) {
StackNode *cur = (StackNode *)(pIt->pStackElement);
assert(cur != NULL);
STACK_ITEM_T item = cur->item;
pIt->pStackElement = cur->next;
return item;
}
void TestIterator(void) {
// Create a stack
struct Stack *pStack = CreateStack();
// Push 20, 24, 90 in turn
StackPush(pStack, 20);
StackPush(pStack, 24);
StackPush(pStack, 90);
// Get an iterator of the stack
StackIterator it = GetIterator(pStack);
// visit each element of the stack: 90, 24, 20
while (HasNext(&it)) {
STACK_ITEM_T item = NextItem(&it);
printf("NextItem(it) = %ld\n", (long) item);
}
// All the elements are still on the stack
PrintStack(pStack);
// Release the heap space
ReleaseStack(pStack);
}Output:
// visit each element of the stack: 90, 24, 20
NextItem(it) = 90
NextItem(it) = 24
NextItem(it) = 20
// All the elements are still on the stack
Stack: 90 24 20
In this project, we implement an iterator to traverse the elements on the data stack, which is used to detect cycles in the function GetNumOfNodesInCycle().
| Visiting 5 (Cycle Detected) |
|---|
| Nodes on call stack: |
 |
Path:
Node 0 --> Node 2 --> Node 1 --> Node 5
Cycle:
Node 2 --> Node 1 --> Node 5 --> Node 2/*
if v is already on stack
return the number of nodes in a cycle
else
return 0
The top element on the stack is 5 and we are testing its adjacent node 2.
----- Test whether node 2 (i.e., v is 2) is on stack -------------
Input:
v == 2
Stack: 5 1 2 0
Output:
NumOfNodesInCycle = 3
------------------------------------------------------------------
*/
static int GetNumOfNodesInCycle(struct Graph *pGraph, long v, struct Stack *pNodesOnStack) {
// Not used now.
(void) pGraph;
// number of node in a cycle
int n = 0;
// whether v is on stack
int isOnStack = 0;
// Get an iterator of the stack
StackIterator it = GetIterator(pNodesOnStack);
// visit each element
while (HasNext(&it)) {
STACK_ITEM_T nodeId = NextItem(&it);
n++;
if (nodeId == v) {
isOnStack = 1;
break;
//return n;
}
}
if (!isOnStack) {
n = 0;
}
printf("\n----- Test whether node %ld is on stack: NumOfNodesInCycle = %d -----\n", v, n);
PrintStack(pNodesOnStack);
printf("------------------------------------------------------------------\n\n");
return n;
} In an undirected graph,
an edge 'n0 -- n2' is represented as two directed edges:
n0 -> n2
n2 -> n0
We should not treat n2 -> n0 and n0 -> n2 as a cycle in an undirected edge.
Example:
| Visiting 5 (Special Case) |
|---|
| Nodes on call stack: |
 |
Path:
Node 0 --> Node 2 --> Node 1 --> Node 5
Special Case:
Node 1 --> Node 5 --> Node 1
When
GetNumOfNodesInCycle(struct Graph *pGraph, long v, struct Stack *pNodesOnStack) returns 2
and pGraph is an undirected graphThe top element on the stack is 5 and we are testing its adjacent node 1.
----- Test whether node 1 is on stack: NumOfNodesInCycle = 2 -----
Stack: 5 1 2 0
So, Node 1 --> Node 5 --> Node 1 is not treated as a cycle in an undirected graph.
1 How to download this project in CSE VLAB
Open a terminal (Applications -> Terminal Emulator)
$ git clone https://github.com/sheisc/COMP9024.git
$ cd COMP9024/Graphs/CycleDetection
CycleDetection$
2 How to start Visual Studio Code to browse/edit/debug a project.
CycleDetection$ code
Two configuration files (CycleDetection/.vscode/launch.json and CycleDetection/.vscode/tasks.json) have been preset.
In the window of Visual Studio Code, please click "File" and "Open Folder",
select the folder "COMP9024/Graphs/CycleDetection", then click the "Open" button.
click Terminal -> Run Build Task
Open src/Graph.c, and click to add a breakpoint (say, line 337).
Then, click Run -> Start Debugging
├── Makefile defining set of tasks to be executed (the input file of the 'make' command)
|
├── README.md introduction to this tutorial
|
├── images *.dot and *.png files generated by this program
|
├── src containing *.c and *.h
| |
| ├── Graph.c Cycle detection
| ├── Graph.h
| ├── Stack.c For recording nodes on the call stack
| ├── Stack.h
| ├── main.c main()
|
└── .vscode containing configuration files for Visual Studio Code
|
├── launch.json specifying which program to debug and with which debugger,
| used when you click "Run -> Start Debugging"
|
└── tasks.json specifying which task to run (e.g., 'make' or 'make clean')
used when you click "Terminal -> Run Build Task" or "Terminal -> Run Task"Makefile is discussed in COMP9024/C/HowToMake.
In addition to utilizing VS Code, we can also compile and execute programs directly from the command line interface as follows.
CycleDetection$ make
CycleDetection$ ./main
Click on the window of 'feh' or use your mouse scroll wheel to view images.
Here, feh is an image viewer available in CSE VLAB.
Ensure that you have executed 'make' and './main' before 'make view'.
| Initial |
|---|
 |
| Visiting 0 | Visiting 2 |
|---|---|
| Nodes on call stack: |
Nodes on call stack: |
 |
 |
| Visiting 1 | Visiting 5 |
|---|---|
| Nodes on call stack: |
Nodes on call stack: |
 |
 |
| Visiting 4 (Cycle Detected) | Visiting 7 |
|---|---|
| Nodes on call stack: |
Nodes on call stack: |
 |
 |
| Visiting 6 (Cycle Detected) | Visiting 3 |
|---|---|
| Nodes on call stack: |
Nodes on call stack: |
 |
 |
| Call Tree and Directed Graph |
|---|
 |
CycleDetection$ make
CycleDetection$ ./main
########################### TestCycleDetection(directed) ######################
********** The Adjacency Matrix *************
0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0
0 1 0 0 1 1 0 0
1 0 0 0 0 0 0 0
1 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
****** Graph Nodes ********
Graph Node 0: 0
Graph Node 1: 1
Graph Node 2: 2
Graph Node 3: 3
Graph Node 4: 4
Graph Node 5: 5
Graph Node 6: 6
Graph Node 7: 7
----- Test whether node 0 is on stack: NumOfNodesInCycle = 3 -----
Stack: 4 2 0
------------------------------------------------------------------
****************** Cycle 1 detected (directed) *****************
Stack: 4 2 0
node 0 is on stack
Nodes in a cycle:
4 2 0
****************************************************************
----- Test whether node 2 is on stack: NumOfNodesInCycle = 4 -----
Stack: 6 7 4 2 0
------------------------------------------------------------------
****************** Cycle 2 detected (directed) *****************
Stack: 6 7 4 2 0
node 2 is on stack
Nodes in a cycle:
6 7 4 2
****************************************************************
----- Test whether node 5 is on stack: NumOfNodesInCycle = 0 -----
Stack: 2 0
------------------------------------------------------------------
----- Test whether node 0 is on stack: NumOfNodesInCycle = 0 -----
Stack: 3
------------------------------------------------------------------
The graph is cyclic.
CycleDetection$ make view
find . -name "*.png" | sort | xargs feh -g 720x540 &
CycleDetection$ find . -name "*.c" -or -name "*.h" | xargs cat | wc -l
819
Click on the window of 'feh' or use your mouse scroll wheel to view images.
Here, feh is an image viewer available in CSE VLAB.
Ensure that you have executed 'make' and './main' before 'make view'.
| Initial |
|---|
 |
| Visiting 0 | Visiting 2 |
|---|---|
| Nodes on call stack: |
Nodes on call stack: |
 |
 |
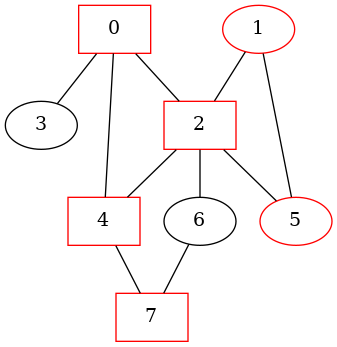
| Visiting 1 | Visiting 5 (Cycle Detected) |
|---|---|
| Nodes on call stack: |
Nodes on call stack: |
 |
 |
| Visiting 4 (Cycle Detected) | Visiting 7 |
|---|---|
| Nodes on call stack: |
Nodes on call stack: |
 |
 |
| Visiting 6 (Cycle Detected) | Visiting 3 |
|---|---|
| Nodes on call stack: |
Nodes on call stack: |
 |
 |
| Call Tree and Undirected Graph |
|---|
 |
########################### TestCycleDetection(undirected) ######################
********** The Adjacency Matrix *************
0 0 1 1 1 0 0 0
0 0 1 0 0 1 0 0
1 1 0 0 1 1 1 0
1 0 0 0 0 0 0 0
1 0 1 0 0 0 0 1
0 1 1 0 0 0 0 0
0 0 1 0 0 0 0 1
0 0 0 0 1 0 1 0
****** Graph Nodes ********
Graph Node 0: 0
Graph Node 1: 1
Graph Node 2: 2
Graph Node 3: 3
Graph Node 4: 4
Graph Node 5: 5
Graph Node 6: 6
Graph Node 7: 7
----- Test whether node 0 is on stack: NumOfNodesInCycle = 2 -----
Stack: 2 0
------------------------------------------------------------------
----- Test whether node 2 is on stack: NumOfNodesInCycle = 2 -----
Stack: 1 2 0
------------------------------------------------------------------
----- Test whether node 1 is on stack: NumOfNodesInCycle = 2 -----
Stack: 5 1 2 0
------------------------------------------------------------------
----- Test whether node 2 is on stack: NumOfNodesInCycle = 3 -----
Stack: 5 1 2 0
------------------------------------------------------------------
****************** Cycle 1 detected (undirected) *****************
Stack: 5 1 2 0
node 2 is on stack
Nodes in a cycle:
5 1 2
****************************************************************
----- Test whether node 0 is on stack: NumOfNodesInCycle = 3 -----
Stack: 4 2 0
------------------------------------------------------------------
****************** Cycle 2 detected (undirected) *****************
Stack: 4 2 0
node 0 is on stack
Nodes in a cycle:
4 2 0
****************************************************************
----- Test whether node 2 is on stack: NumOfNodesInCycle = 2 -----
Stack: 4 2 0
------------------------------------------------------------------
----- Test whether node 4 is on stack: NumOfNodesInCycle = 2 -----
Stack: 7 4 2 0
------------------------------------------------------------------
----- Test whether node 2 is on stack: NumOfNodesInCycle = 4 -----
Stack: 6 7 4 2 0
------------------------------------------------------------------
****************** Cycle 3 detected (undirected) *****************
Stack: 6 7 4 2 0
node 2 is on stack
Nodes in a cycle:
6 7 4 2
****************************************************************
----- Test whether node 7 is on stack: NumOfNodesInCycle = 2 -----
Stack: 6 7 4 2 0
------------------------------------------------------------------
----- Test whether node 5 is on stack: NumOfNodesInCycle = 0 -----
Stack: 2 0
------------------------------------------------------------------
----- Test whether node 6 is on stack: NumOfNodesInCycle = 0 -----
Stack: 2 0
------------------------------------------------------------------
----- Test whether node 0 is on stack: NumOfNodesInCycle = 2 -----
Stack: 3 0
------------------------------------------------------------------
----- Test whether node 4 is on stack: NumOfNodesInCycle = 0 -----
Stack: 0
------------------------------------------------------------------
The graph is cyclic.// Storing information of a graph node
struct GraphNode {
char name[MAX_ID_LEN + 1];
int onstack;
};
typedef long AdjMatrixElementTy;
struct Graph{
/*
Memory Layout:
-----------------------------------------------------------
pAdjMatrix ----> Element(0, 0), Element(0, 1), ..., Element(0, n-1), // each row has n elements
Element(1, 0), Element(1, 1), ..., Element(1, n-1),
..... Element(u, v) ... // (n * u + v) elements away from Element(0, 0)
Element(n-1, 0), Element(n-1, 1), ..., Element(n-1, n-1)
-----------------------------------------------------------
Adjacency Matrix on Heap
*/
AdjMatrixElementTy *pAdjMatrix;
/*
Memory Layout
---------------------------
pNodes[n-1]
pNodes[1]
pNodes -----> pNodes[0]
----------------------------
struct GraphNode[n] on Heap
*/
struct GraphNode *pNodes;
// number of nodes
long n;
// whether it is a directed graph
int isDirected;
};
// 0 <= u < n, 0 <= v < n
// ELement(u, v) is (n * u + v) elements away from Element(0, 0)
#define MatrixElement(pGraph, u, v) (pGraph)->pAdjMatrix[(pGraph)->n * (u) + (v)]MatrixElement(pGraph, u, v) is a macro, not a function call.
For example,
MatrixElement(pGraph, 3 - 1, 1) is expanded as (pGraph)->pAdjMatrix[(pGraph)->n * (3-1) + (1)] by the C preprocessor.
If MatrixElement(pGraph, u, v) is defined as (pGraph)->pAdjMatrix[(pGraph)->n * u + v],
MatrixElement(pGraph, 3 - 1, 1) will be expanded as (pGraph)->pAdjMatrix[(pGraph)->n * 3 - 1 + 1].
Apparently, (pGraph)->pAdjMatrix[(pGraph)->n * 3 - 1 + 1] is not the element the C programmer wants to access.
That is why we need to add a pair of parentheses for pGraph, u, and v in (pGraph)->pAdjMatrix[(pGraph)->n * (u) + (v)].
// test.c
#define MUL(a, b) a * b
int add(int a, int b) {
return a + b;
}
int r;
int main(void) {
r = MUL(3-1, 2-1); // bug
r = add(3-1, 2-1);
return 0;
}$ gcc -E test.c
int add(int a, int b) {
return a + b;
}
int r;
int main(void) {
r = 3-1 * 2-1;
r = add(3-1, 2-1);
return 0;
}
#define CONNECTED 1
#define NUM_OF_NODES 8
int TestCycleDetection(int isDirected) {
// Create a directed graph with 8 nodes
struct Graph *pGraph = CreateGraph(NUM_OF_NODES, isDirected);
//char *nodeNames[NUM_OF_NODES] = {"A", "B", "C", "D", "E", "F", "G", "H"};
char *nodeNames[NUM_OF_NODES] = {"0", "1", "2", "3", "4", "5", "6", "7"};
// Add nodes
for (long u = 0; u < NUM_OF_NODES; u++) {
GraphAddNode(pGraph, u, nodeNames[u]);
}
// edges: source node id, target node id, value of the edge
long edges[][3] = {
{0, 2, CONNECTED},
{1, 5, CONNECTED},
{2, 1, CONNECTED},
{2, 4, CONNECTED},
{2, 5, CONNECTED},
{3, 0, CONNECTED},
{4, 0, CONNECTED},
{4, 7, CONNECTED},
{6, 2, CONNECTED},
{7, 6, CONNECTED},
};
// Add edges
for (long i = 0; i < sizeof(edges)/sizeof(edges[0]); i++) {
GraphAddEdge(pGraph, edges[i][0], edges[i][1], edges[i][2]);
}
PrintGraph(pGraph);
// create a sub-directory 'images' (if it is not present) in the current directory
system("mkdir -p images");
// remove the *.dot and *.png files in the directory 'images'
//system("rm -f images/*.dot images/*.png");
if (HasCycle(pGraph)) {
printf("The graph is cyclic.\n");
} else {
printf("The graph is acyclic.\n");
}
ReleaseGraph(pGraph);
//TestIterator();
return 0;
}
int main(void) {
// directed graph
TestCycleDetection(1);
// undirected graph
TestCycleDetection(0);
return 0;
}The DetectCycle() function is implemented recursively for DFS traversal to detect cycles.
As it is hard to access the nodes on the call stack, we create a data stack to record the nodes.
When entering the function DetectCycle(), the current node is pushed onto the data stack.
When DetectCycle() returns, the node is popped from the data stack.
In an undirected graph,
an edge 'n0 -- n2' is represented as two directed edges:
n0 -> n2
n2 -> n0
We should not treat n2 -> n0 and n0 -> n2 as a cycle in an undirected edge.Whether the cycle detection stops after finding the first cycle.
/*
if v is already on stack
return the number of nodes in a cycle
else
return 0
----- Test whether node 2 is on stack: NumOfNodesInCycle = 3 -----
Stack: 5 1 2 0
------------------------------------------------------------------
*/
static int GetNumOfNodesInCycle(struct Graph *pGraph, long v, struct Stack *pNodesOnStack) {
// Not used now.
(void) pGraph;
// number of node in a cycle
int n = 0;
// whether v is on stack
int isOnStack = 0;
// Get an iterator of the stack
StackIterator it = GetIterator(pNodesOnStack);
// visit each element
while (HasNext(&it)) {
STACK_ITEM_T nodeId = NextItem(&it);
n++;
if (nodeId == v) {
isOnStack = 1;
break;
//return n;
}
}
if (!isOnStack) {
n = 0;
}
printf("\n----- Test whether node %ld is on stack: NumOfNodesInCycle = %d -----\n", v, n);
PrintStack(pNodesOnStack);
printf("------------------------------------------------------------------\n\n");
return n;
}
//#define STOP_DETECTION_AT_FIRST_CYCLE
static long cycles = 0;
static long imgCnt = 0;
/*
Input
v == 2
Stack: 6 7 4 2 0
Output
Nodes in a cycle:
6 7 4 2
*/
static void PrintNodesInCycle(struct Graph *pGraph, long v, struct Stack *pNodesOnStack) {
// Get an iterator of the stack
StackIterator it = GetIterator(pNodesOnStack);
cycles++;
if (pGraph->isDirected) {
printf("\n\t\t****************** Cycle %ld detected (directed) *****************\n\t\t", cycles);
} else {
printf("\n\t\t****************** Cycle %ld detected (undirected) *****************\n\t\t", cycles);
}
/*
v == 2
Stack: 6 7 4 2 0
Nodes in a cycle:
6 7 4 2
*/
PrintStack(pNodesOnStack);
printf("\t\tnode %ld is on stack\n", v);
printf("\t\tNodes in a cycle: \n\t\t");
// visit each element
while (HasNext(&it)) {
STACK_ITEM_T nodeId = NextItem(&it);
printf("%ld ", nodeId);
if (nodeId == v) {
break;
}
}
printf("\n\t\t****************************************************************\n");
}
static int DetectCycle(struct Graph *pGraph, long u, int *visited, struct Stack *pNodesOnStack) {
visited[u] = 1;
pGraph->pNodes[u].onstack = 1;
// Push u onto the data stack
StackPush(pNodesOnStack, u);
imgCnt++;
if (pGraph->isDirected) {
GenOneImage(pGraph, "HasCycleDirected", "images/HasCycleDirected", imgCnt, visited);
} else {
GenOneImage(pGraph, "HasCycleUndirected", "images/HasCycleUndirected", imgCnt, visited);
}
int cycleDetected = 0;
// recursively visit the adjacent nodes of u, if they have not been visited yet
for(long v = 0; v < pGraph->n; v++) {
if (MatrixElement(pGraph, u, v)) {
if (!visited[v]) {
if (DetectCycle(pGraph, v, visited, pNodesOnStack)) {
cycleDetected = 1;
#ifdef STOP_DETECTION_AT_FIRST_CYCLE
break;
#endif
}
} else {
int nodesInCycle = GetNumOfNodesInCycle(pGraph, v, pNodesOnStack);
if (nodesInCycle > 0) {
if (!pGraph->isDirected) {
/*
In an undirected graph,
an edge 'n0 -- n2' is represented as two directed edges:
n0 -> n2
n2 -> n0
We should not treat n2 -> n0 and n0 -> n2 as a cycle in an undirected edge.
So we need to check it here.
*/
if (nodesInCycle == 2) {
continue;
}
}
PrintNodesInCycle(pGraph, v, pNodesOnStack);
cycleDetected = 1;
#ifdef STOP_DETECTION_AT_FIRST_CYCLE
break;
#endif
}
}
}
}
StackPop(pNodesOnStack);
pGraph->pNodes[u].onstack = 0;
return cycleDetected;
}
int HasCycle(struct Graph *pGraph) {
int cyclic = 0;
int *visited = (int *) malloc(pGraph->n * sizeof(int));
struct Stack *pNodesOnStack = CreateStack();
//memset(visited, 0, sizeof(int) * pGraph->n);
for (long v = 0; v < pGraph->n; v++) {
visited[v] = 0;
pGraph->pNodes[v].onstack = 0;
}
imgCnt = 0;
cycles = 0;
if (pGraph->isDirected) {
GenOneImage(pGraph, "HasCycleDirected", "images/HasCycleDirected", imgCnt, visited);
} else {
GenOneImage(pGraph, "HasCycleUndirected", "images/HasCycleUndirected", imgCnt, visited);
}
for (long u = 0; u < pGraph->n; u++) {
if (!visited[u]) {
if (DetectCycle(pGraph, u, visited, pNodesOnStack)) {
cyclic = 1;
#ifdef STOP_DETECTION_AT_FIRST_CYCLE
break;
#endif
}
}
}
free(visited);
//assert(StackIsEmpty(pNodesOnStack));
ReleaseStack(pNodesOnStack);
return cyclic;
}