Playing with Low-density parity-check codes

To study LDPC codes I've started implementing a soft decision decoder using floating point operations only.

For better speed (at almost the same decoding performance) I've added support for saturating fixed-point operations.

SIMD acceleration for floating and fixed-point is in the works.

You can switch between six Belief propagation algorithms:

• min-sum algorithm: using minimum and addition
• self-corrected min-sum algorithm: using minimum, addition and erasures
• min-sum-c algorithm: using minimum, addition and a correction factor
• sum-product algorithm: using tanh+atanh-functions, addition and multiplication
• log-sum-product algorithm: using log+exp-functions to replace above multiplication with addition in the log domain
• lambda-min algorithm: same as log-sum-product, but using only lambda minima

Decoding speed varies about 10ms (no errors) to 300ms (max errors) for the rate 1/2 N=64800 code using self-corrected min-sum on my workstation.

Here some good reads:

• Low-Density Parity-Check Codes
  by Robert G. Gallager - 1963
• Near Shannon Limit Performance of Low Density Parity Check Codes
  by David J.C. MacKay and Radford M. Neal - 1996
• An introduction to LDPC codes
  by William E. Ryan - 2003
• DVB-S2 Low Density Parity Check Codes with near Shannon Limit Performance
  by Mustafa Eroz, Feng-Wen Sun and Lin-Nan Lee - 2004
• Self-Corrected Min-Sum decoding of LDPC codes
  by Valentin Savin - 2008
• en_302307v010201p.pdf
• a83-1_dvb-s2_den302307v141.pdf
• en_30230702v010101a.pdf
• en_302755v010401p.pdf

BER comparison of the various algorithms

The following plots were made by computing MS, MSC, SCMS and SCMSC with fixed-point saturating arithmetics using a factor of 2 while SP and SCSP are computed using double precision floating-point arithmetics.

Used DVB-S2 B4 table, QPSK modulation and averaged over 1000 blocks:

To better see the behaviour at low SNR, here with a linear BER scale:

To better see the waterfall region and the boundary to quasi-errorless decoding, here the logarithmic BER scale:

Impact of the varying degrees of the bit nodes on their convergence behaviour

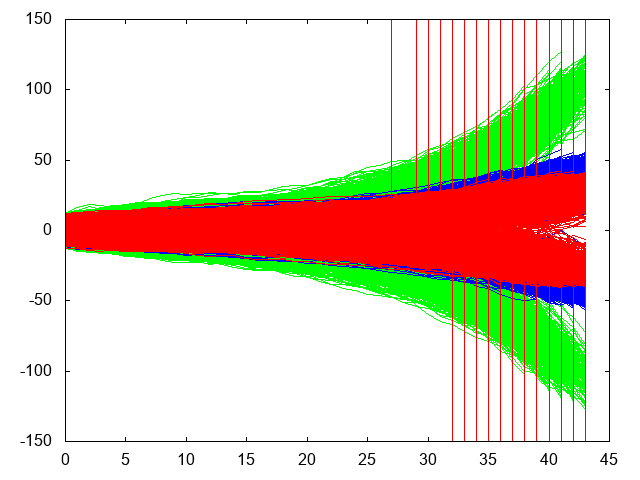
The color on the following three plots are to be interpreted like this:

• Red: parity bit nodes with degree two
• Green: message bit nodes with degree eight
• Blue: message bit nodes with degree three

This is the second fastest algorithm, min-sum-c, but it needs a few iterations longer to converge:

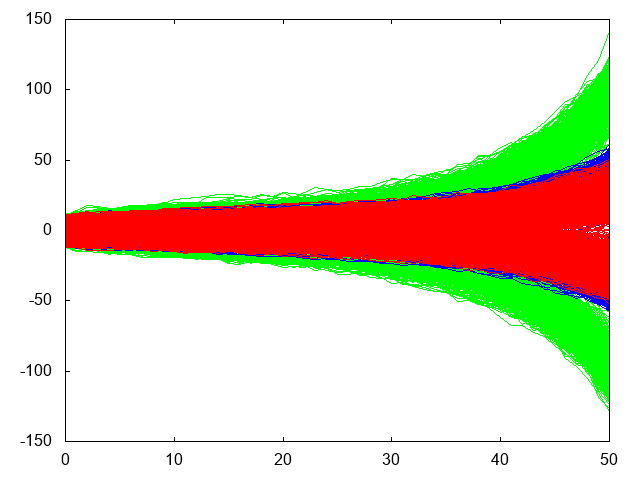
The sum-product algorithms converge much faster than the min-sum algorithms, but they involve transcendental functions.

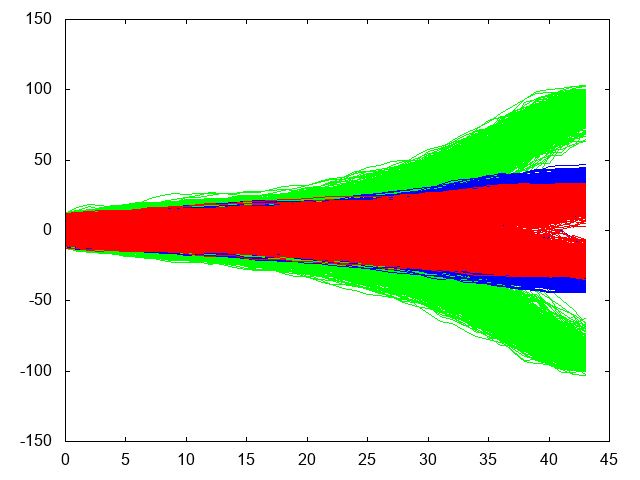
Here we see the fastest convergence, where bit nodes go to minus or plus infinity (and sometimes back from):

Getting soft information from symbols

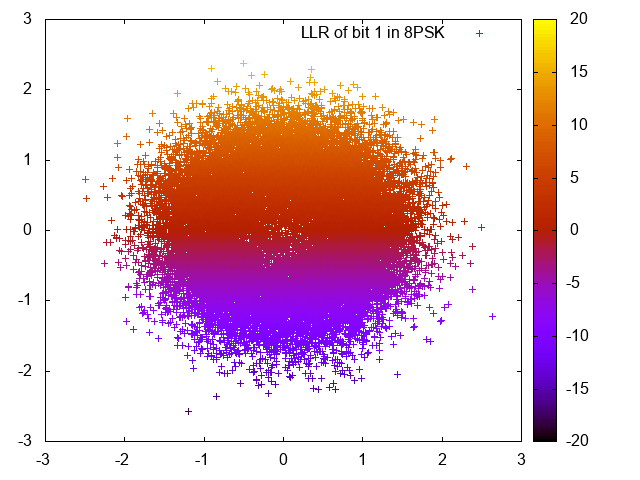
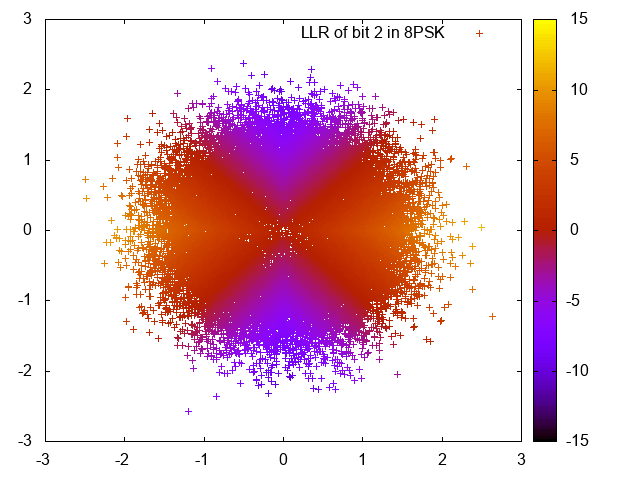
For the LDPC codes to work best, one needs soft reliability information for each bit.

Here we see the log-likelihood ratios of the different bits of many 8PSK modulated symbols, disturbed by AWGN:

exclusive_reduce.hh

Reduce N times while excluding ith input element

It computes the following, but having only O(N) complexity and using O(1) extra storage:

	output[0] = input[1];
	output[1] = input[0];
	for (int i = 2; i < N; ++i)
		output[i] = op(input[0], input[1]);
	for (int i = 0; i < N; ++i)
		for (int j = 2; j < N; ++j)
			if (i != j)
				output[i] = op(output[i], input[j]);