RSOpt (Riemannian stochastic optimization algorithms)

The codes will be uploaded soon!!

Authors: Hiroyuki Kasai

Last page update: July 12, 2018

Latest version: 1.0.0 (see Release notes for more info)

Algorithms

• R-SGD (Riemannian stochastic gradient descent) algorithm

  • S.Bonnabel, "Stochastic gradient descent on Riemannian manifolds," IEEE Trans. on Auto. Cont., 2013.

• R-SVRG (Riemannian stochastic variance reduced gradient) algorithm

  • H.Sato, H.Kasai and B.Mishra, "Riemannian stochastic variance reduced gradient," arXiv:1702.05594, 2017.
  • H.Kasai, H.Sato and B.Mishra, "Riemannian stochastic variance reduced gradient on Grassmann manifold," NIPS workshop OPT2016, 2016.
  • H.Zhang, S.J.Reddi and S.Sra, "Fast stochastic optimization on Riemannian manifolds," NIPS2016, 2016.

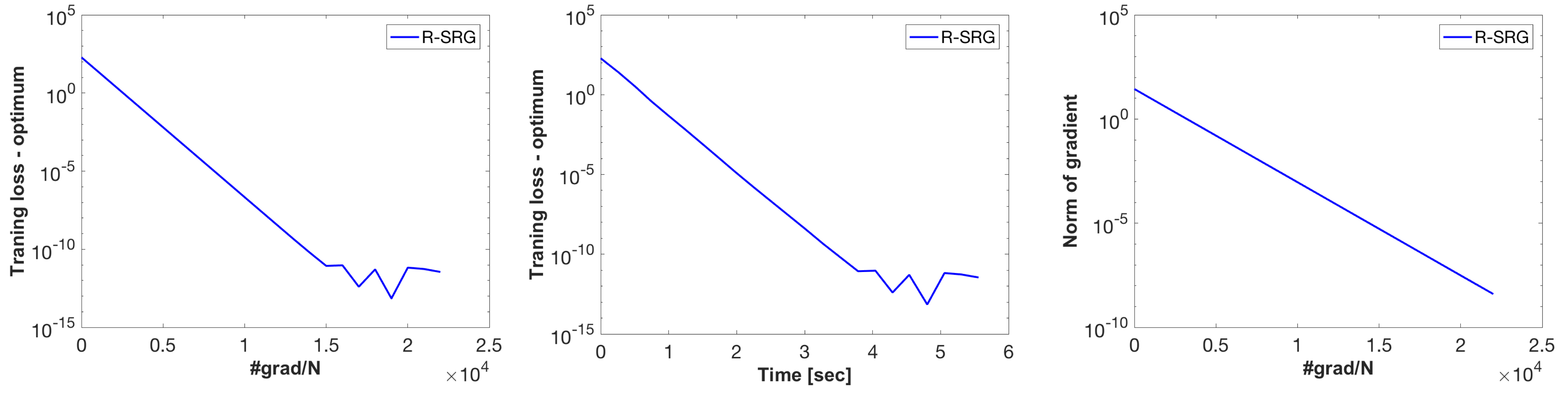
• R-SRG (Riemannian stochastic recursive gradient) algorithm

  • H.Kasai, H.Sato and B.Mishra, "Riemannian stochastic recursive gradient algorithm," ICML2018, 2018.

• R-SQN-VR (Riemannian stochastic quasi-Newton algorithm with variance reduction) algorithm

  • H.Kasai, H.Sato and B.Mishra, "Riemannian stochastic quasi-Newton algorithm with variance reduction and its convergence analysis," AISTATS2018, 2018.

Folders and files

./                      - Top directory.
./README.md             - This readme file.
./run_me_first.m        - The scipt that you need to run first.
./demo.m                - Demonstration script to check and understand this package easily. 
|solvers/               - Contains various Riemannian stochastic optimization algorithms.
|tool/                  - Some auxiliary tools for this project.
|manopt/                - Contains manopt toolbox.

First to do

Run run_me_first for path configurations.

%% First run the setup script
run_me_first; 

Demonstration script

Run demo for computing the N Riemannian centroid on the dxd symmetric positive-definite (SPD) manifold. This problem frequently appears in computer vision problems such as visual object categorization and pose categorization. This demonstation handles N=500 and d=3.

demo; 

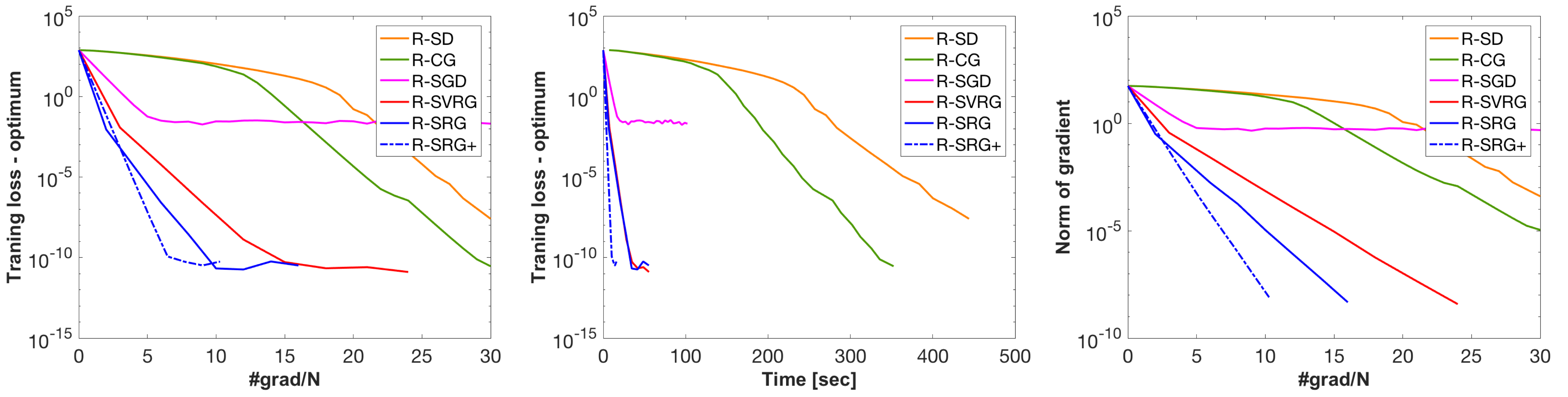
More plots

Run show_centroid_plots for the same Riemannian centroid problem. This scripts compares R-SGD, R-SVRG, R-SRG and R-SRG+ as well as batch algorithms including R-SD and R-CG. This scripts handles N=5000 and d=10.

show_centroid_plots; 

License

• The code is free and open source.
• The code should only be used for academic/research purposes.

Notes

• The code is compliant to manopt project.

Problems or questions

If you have any problems or questions, please contact the author: Hiroyuki Kasai (email: kasai at is dot uec dot ac dot jp)

Release Notes

• Version 1.0.0 (July 12, 2018)
  • Initial version.