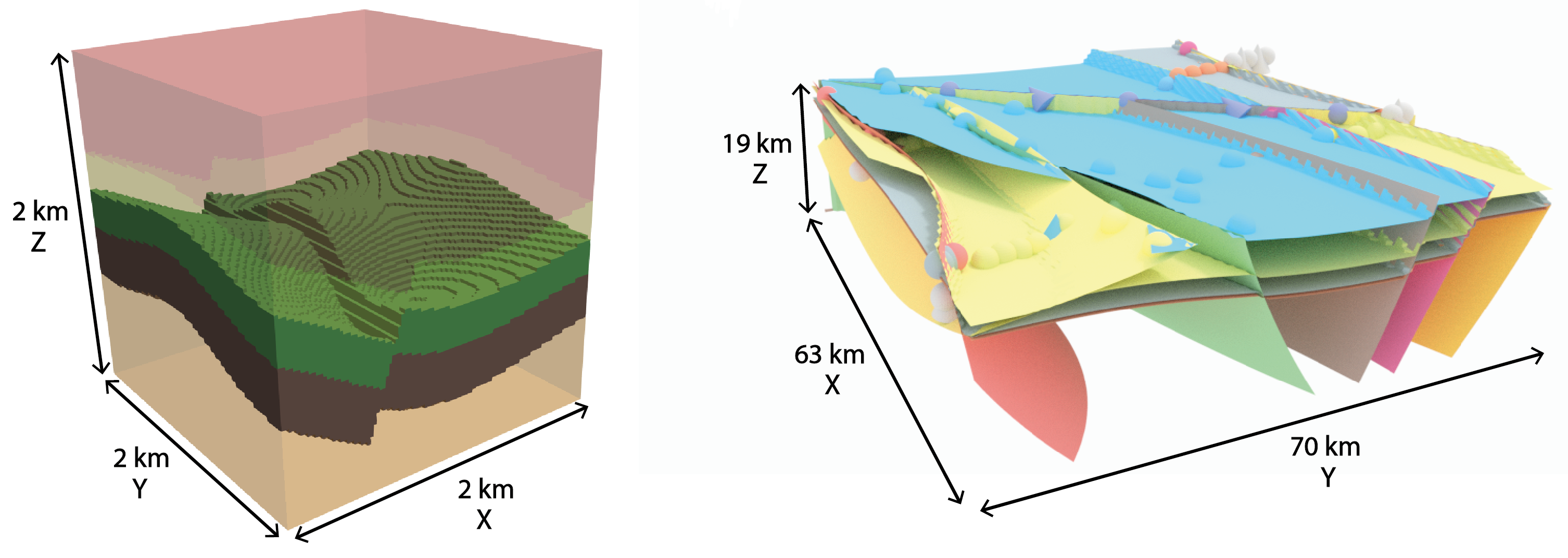
Open-source, implicit 3D structural geological modeling in Python for uncertainty analysis.
GemPy is a Python-based, open-source geomodeling library. It is
capable of constructing complex 3D geological models of folded
structures, fault networks and unconformities, based on the underlying
powerful implicit representation approach. GemPy was designed from the
ground up to support easy embedding in probabilistic frameworks for the
uncertainty analysis of subsurface structures.
Check out the documentation either in the main website gempy.org (better option), or the specific docs site.
GemPy enables the modeling of complex 3D geological settings,
on par with many commercial geomodeling packages, including:
- Multiple conformal layers (e.g. sequences of sedimentary layers)
- Several sequences of layers, with conformal continuation or unconformities
- Magmatic bodies of (almost) arbitrary shapes
- Faults (offset calculated automatically from affected geological objects)
- Full fault networks (faults affecting faults)
- Folds (affecting single layers or entire layer stacks, including overturned and recumbent folds)
The combination of these elements allows for the generation of realistic 3-D geological models in most typical geological settings.
The generation of complex structural settings is based on the powerful
interpolation algorithm underlying GemPy, a universal cokriging method
devoised by Lajaunie et al. (1997) and extended by Calcagno et al. (2008).
This method is used to interpolate a 3D scalar field, such that geologically
significant interfaces are isosurfces in this field.
The algorithm allows for a direct integration of two of the most relevant geological input data types:
- Surface contact points: 3D coordinates of points marking the boundaries between different features (e.g. layer interfaces, fault planes, unconformities).
- Orientation measurements: Orientation of the poles perpendicular to the dipping of surfaces at any point in the 3D space.
GemPy also allows for the definition of topological elements such as
combining multiple stratigraphic sequences and
complex fault networks to be considered in the modeling process.
Models generated with GemPy can be visualized in several ways:
- direct visualization of 2D model sections (or geological maps) using
matplotlib, including hillshading and other options for intuitive representation of results; - interactive 3D visualization and model input manipulation using the Visualization Toolkit (VTK);
- We also actively develop a link to the fantastic
pyvistaproject for even better visualization and model interaction in 3D.
In addition to visualization, the generated models can be exported in a variety of ways:
- Export of VTK files for further visualization and processing in other software such as ParaView;
- Export of triangulated surface meshes (e.g. for further processing in meshing programs);
- Export of images (e.g. geological maps) for
We are also currently working on a tighter integration wtih several
meshing libraries, notably CGAL and
gmesh. In addition, we have established
links to several other open-source libraries, including pygimli
for geophysical modeling and inversion. In the current state, however, these
links have to be considered as highly experimental and they are not yet
part of the stable release. If you are interested in these features,
feel free to contact us.
One of the most advanced features that sets gempy also apart from
available commercial packages is the full integration of stochastic
geological modeling methods.
GemPy was designed from the ground up to support stochastic geological
modeling for uncertainty analysis (e.g. Monte Carlo simulations, Bayesian
inference). This was achieved by writing GemPy's core architecture
using the numerical computation library Theano
to couple it with the probabilistic programming
framework PyMC3.
This enables the use of advanced sampling methods (e.g. Hamiltonian Monte
Carlo) and is of particular relevance when considering uncertainties in
the model input data and making use of additional secondary information
in a Bayesian inference framework.
We can, for example, include uncertainties with respect to the z-position of layer boundaries in the model space. Simple Monte Carlo simulation via PyMC will then result in different model realizations.
Theano allows the automated computation of gradients, opening the door to the use of advanced gradient-based sampling methods coupling GeMpy and PyMC3 for advanced stochastic modeling. Also, the use of Theano allows making use of GPUs through cuda (see the Theano documentation for more information.
Making use of vtk interactivity and Qgrid (https://github.com/quantopian/qgrid) ,
GemPy provides a functional interface to interact with input data and models.
For a more detailed elaboration of the theory behind GemPy, we refer to the
open access scientific publication:
"GemPy 1.0: open-source stochastic geological modeling and inversion"
by de la Varga et al. (2018).
We provide the latest release version of GemPy via the Conda and PyPi package services. We highly
recommend using PyPi, as it will take care of automatically installing all dependencies.
$ pip install gempy
You can also visit PyPi <https://pypi.org/project/gempy/>_, or
GitHub <https://github.com/cgre-aachen/gempy>
For more details in the installation check:
Installation <http://docs.pyvista.org/getting-started/installation.html#install-ref.>
Extensive documentation for GemPy is hosted at gempy.readthedocs.io,
explaining its capabilities, the theory behind it and
providing detailed tutorials on how to use it.
- de la Varga, M., Schaaf, A., and Wellmann, F.: GemPy 1.0: open-source stochastic geological modeling and inversion, Geosci. Model Dev., 12, 1-32, https://doi.org/10.5194/gmd-12-1-2019, 2019
- Calcagno, P., Chilès, J. P., Courrioux, G., & Guillen, A. (2008). Geological modelling from field data and geological knowledge: Part I. Modelling method coupling 3D potential-field interpolation and geological rules. Physics of the Earth and Planetary Interiors, 171(1-4), 147-157.
- Lajaunie, C., Courrioux, G., & Manuel, L. (1997). Foliation fields and 3D cartography in geology: principles of a method based on potential interpolation. Mathematical Geology, 29(4), 571-584.
- Wellmann, F., Schaaf, A., de la Varga, M., & von Hagke, C. (2019). From Google Earth to 3D Geology Problem 2: Seeing Below the Surface of the Digital Earth. In Developments in Structural Geology and Tectonics (Vol. 5, pp. 189-204). Elsevier.