A Binary Heap is a heap data structure that takes the form of a binary tree (Note: Not a binary search tree). Priority queues are efficiently implemented using Binary Heap. Priority queues are useful for any application that involves processing elements based on some priority.
The binary heap is a binary tree that satisfies the following conditions:
A binary heap is a complete binary tree; all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
The key stored in each node is either greater than or equal to (≥) or less than or equal to (≤) the keys in the node's children.
i.e. the ordering is one of two types:
- min-heap property: the value of each node is greater than or equal to the value of its parent, with the minimum-value element at the root. This same property is recursively true for all nodes in the Binary Tree.
- max-heap property: the value of each node is less than or equal to the value of its parent, with the maximum-value element at the root. This same property is recursively true for all nodes in the Binary Tree.
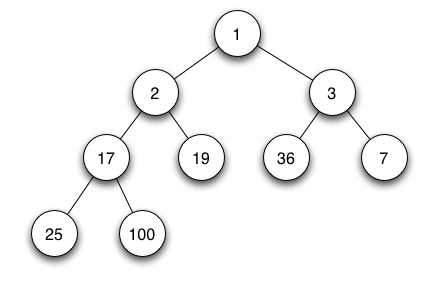
An example of a Minimum Binary Heap:
Heaps are commonly implemented using an array. No space is required for pointers; instead, the parent and children of each node can be found by arithmetic on array indices.
Let n be the number of elements in the heap and i be an arbitrary valid index of the array storing the heap. If the tree root is at index 1, with valid indices 1 through n, then --
- For any given element at position i its left child is at [2 * i]
- For any given element at position i its right child is at [2 * i +1]
- For any given element at position i its parent node is at [i/2]
Complete Binary Heap stored in an array
Binary Heap and its array representation
Binary Heap Operations:
- Insert Operation
- Delete Operation / Extract Minimum (or Maximum)
- Build Heap (Min-Heapify or Max-Heapify)
- Add the element at the bottom leaf of the Heap.
- Perform the bubble-up operation.
- All Insert Operations must perform bubble-up
Example of Insert for Max-heap - Add new element to end of array (And then perform bubble-up)
- If inserted element is smaller than its parent node in case of Min-Heap OR greater than its parent node in case of Max-Heap, swap the element with its parent.
- Keep repeating the above step, till node reaches its correct position.
Max Heap Property violated - Perform swap which causes element to bubble-up
Repeat till element is in correct position
- For Delete - Find the index of the element to be deleted
OR
- For Extract - Remove the element from the root (It will be minimum in case of Min-Heap and maximum in case of Max-Heap).
Subsequently -
- Take out the last element from the last level in the heap (bottom leaf of the Heap)
- Swap this last element with the element at the index to be deleted (or root)
- Perform bubble-down
- All Delete operations must perform bubble-down
Example of Delete for Max-heap - Move root element to the end
Move last element to root (And then perform bubble-down)
- If the replaced element is greater than any of its child node in case of Min-Heap OR smaller than any of its child node in case of Max-Heap, swap the element with its smallest child (Min-Heap) or with its greatest child (Max-Heap).
- Keep repeating the above step, until the node reaches its correct position.
Max Heap Property violated - Perform swap which causes element to bubble-down. Repeat till element is in correct position
Building a heap from an array of n input elements can be done by starting with an empty heap, then successively inserting each element. However a faster method is to arbitrarily insert the elements into a binary tree, respecting the shape property (represented by an array) and then performing the bubble-down operation. Starting from the lowest level and moving upwards, bubble the root of each subtree downward as in the deletion operation until the heap property (min or max) is restored.
If we are building a minimum binary heap it is called min-heapify and if maximum binary heap - it is max-heapify.