| 排序算法 | 时间复杂度 | 是否基于比较 |
|---|---|---|
| 冒泡、插入、选择 | [y] | |
| 快排、归并 | [y] | |
| 桶、基数、计数 | $O(n) | [x] |
开篇问题:插入排序和冒泡排序的时间复杂度相同,都是
- 最好、最坏、平均情况的时间复杂度
- 时间复杂度的系数、低阶、常数——在渐进复杂度相同的情况下,需要比较系数、低阶和常数
- 比较和交换(移动)的次数——基于比较的排序算法的两种基本操作
是否为原地排序算法(In-place sort algorithm),即算法的空间复杂度是否为
经过排序算法处理后,值相同的元素,在原序列和排序后序列中的相对位置保持不变,则称该排序算法是稳定的。
待排序的
item并不是简单的值,而是一个基于对象中的某个key进行排序时,排序的稳定性就有意义了。
- 每次循环都从序列起始位置开始
- 循环中的每个动作,都对比相邻两个元素的大小是否满足偏序要求,若不满足,则交换顺序
分析:
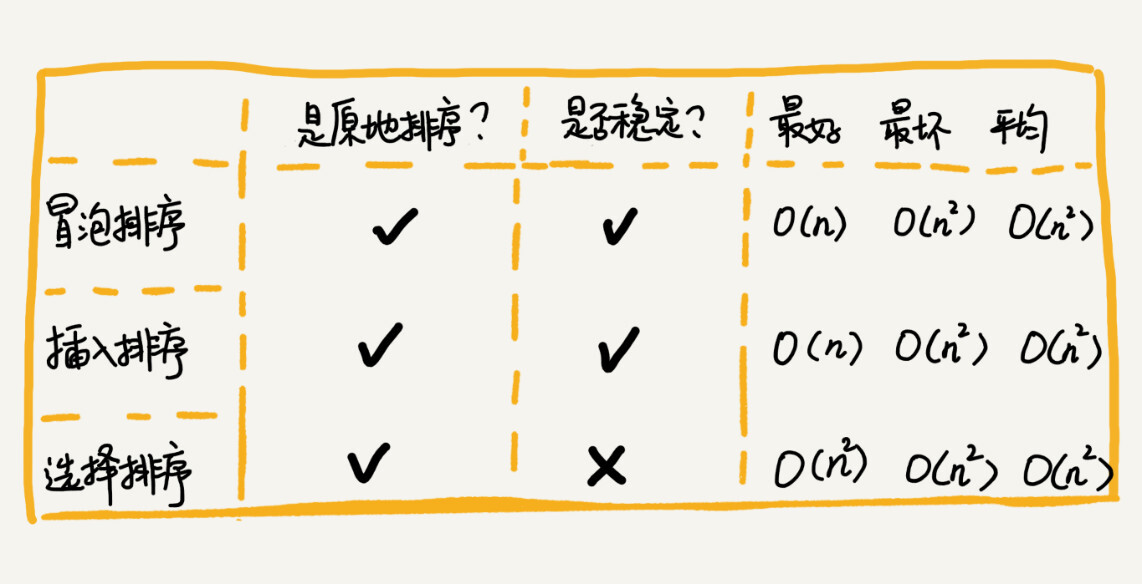
- 原地排序
- 稳定排序(偏序关系是严格的偏序关系,如
<或>) - 时间复杂度
- 最好
$O(n)$ - 最坏
$O(n^2)$ - 平均
$O(n^2)$
- 最好
- 有序度:序列中满足偏序关系的两两组合的元素对的个数
- 满有序度:排序完成的序列的有序度,它等于
$n(n - 1) / 2$ - 逆序度:序列中不满足偏序关系的亮亮组合的元素对的个数
显然,$\text{逆序度} = \text{满有序度} - \text{有序度}$。
在冒泡排序中,每产生一次「交换」操作,$\text{逆序度}--$。于是,平均情况下,需要
分析过程不严格,但足够说明问题。
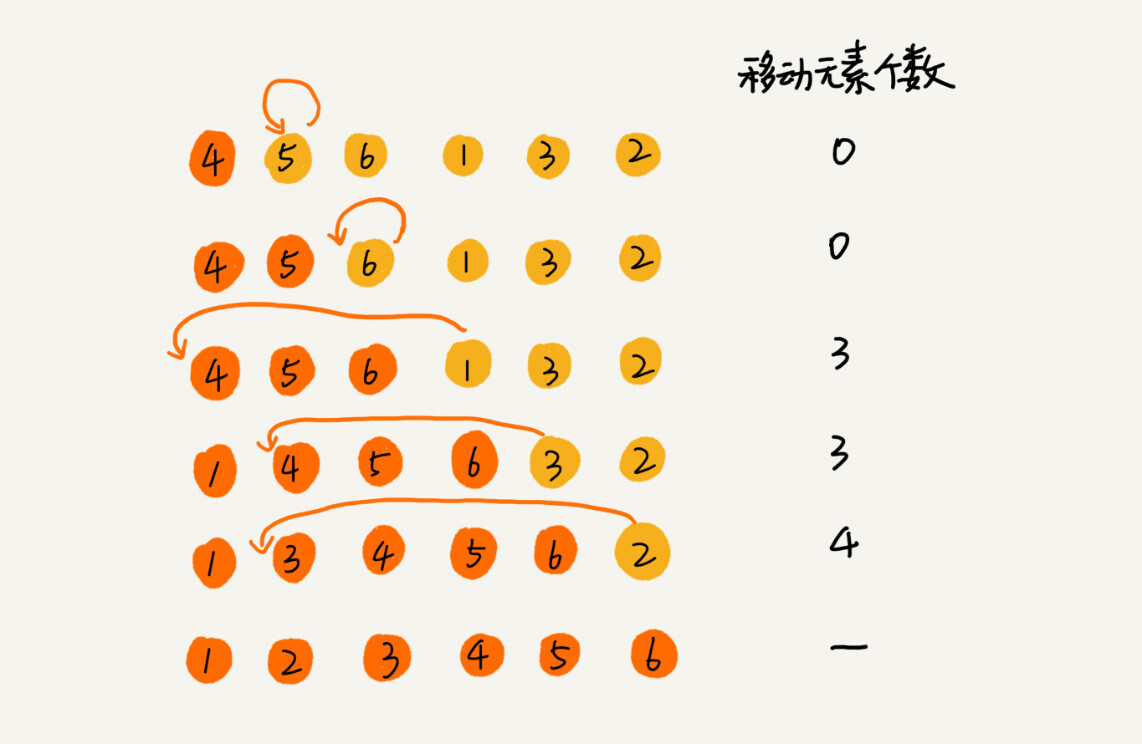
- 将待排序数列分为已排序区间和未排序区间
- 取未排序区间的第一个元素
- 遍历已排序区间,按照偏序关系,寻找合适的位置,插入未排序区间的第一个元素
- 重复 2 -- 3 直至未排序区间长度为零
分析:
- 原地排序
- 稳定排序(值相同的元素,往后插)
- 时间复杂度
- 最好
$O(n)$ - 最坏
$O(n^2)$ - 平均
$O(n^2)$ (乘法法则)
- 最好
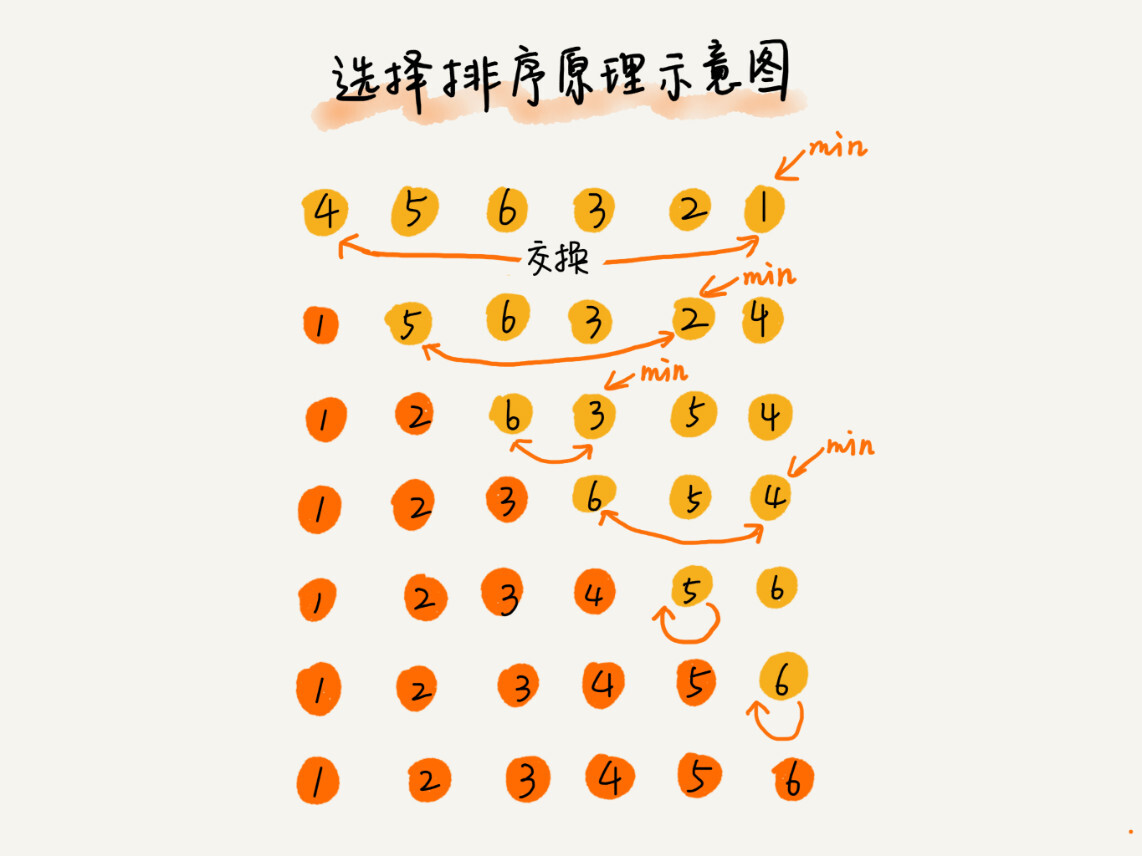
- 将待排序数列分为已排序区间和未排序区间
- 遍历未排序区间,取未排序区间的最小元素
- 交换上述最小元素与未排序区间中的第一个元素的位置
- 重复 2 -- 3 直至未排序区间长度为零
分析:
- 非原地排序
- 非稳定排序
- 时间复杂度
- 最好
$O(n^2)$ - 最坏
$O(n^2)$ - 平均
$O(n^2)$ (乘法法则)
- 最好
- 对同一份未排序序列数据,冒泡排序和插入排序所需的交换(移动)次数是一定的,且是相等的
- 单次数据交换,冒泡排序所需的时间更长(三次赋值操作,插排只需要一次)
另有插入排序的优化版本希尔排序。