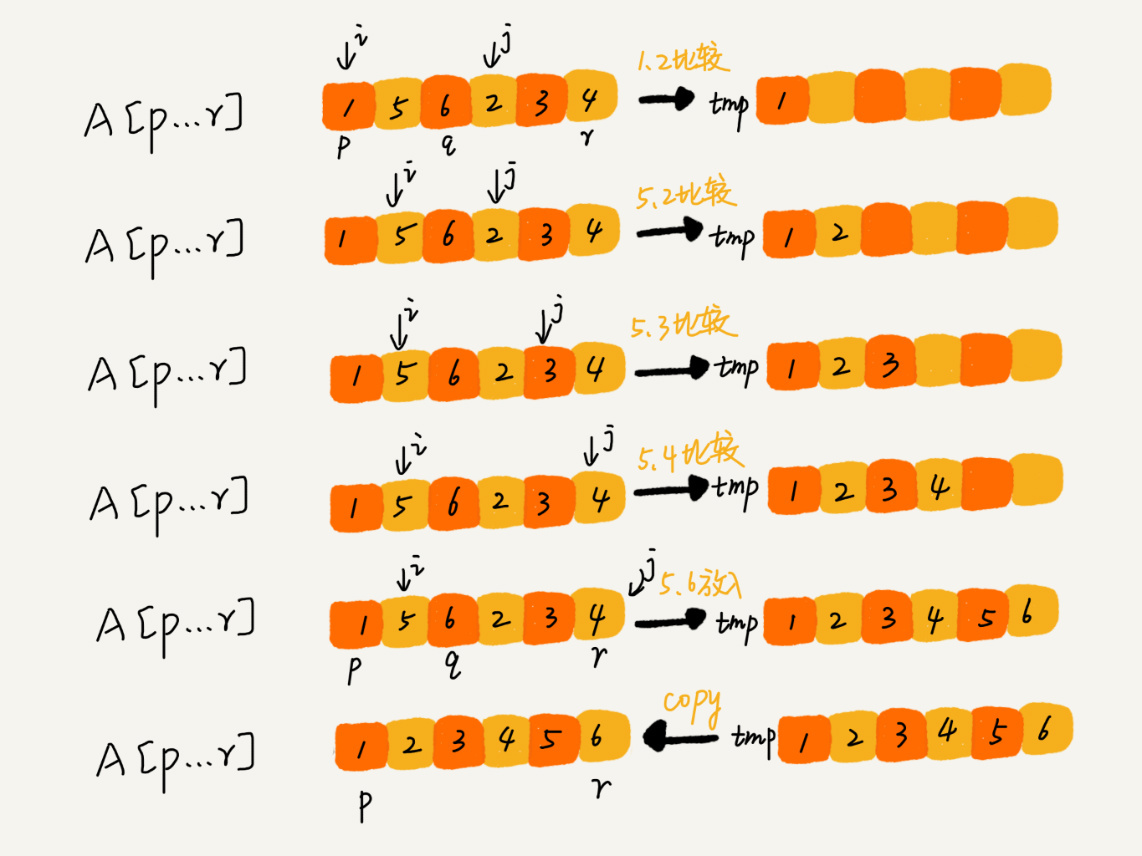排序（线性对数时间复杂度排序算法）

开篇问题：如何在 $O(n)$ 时间复杂度内寻找一个无序数组中第 K 大的元素？

归并排序

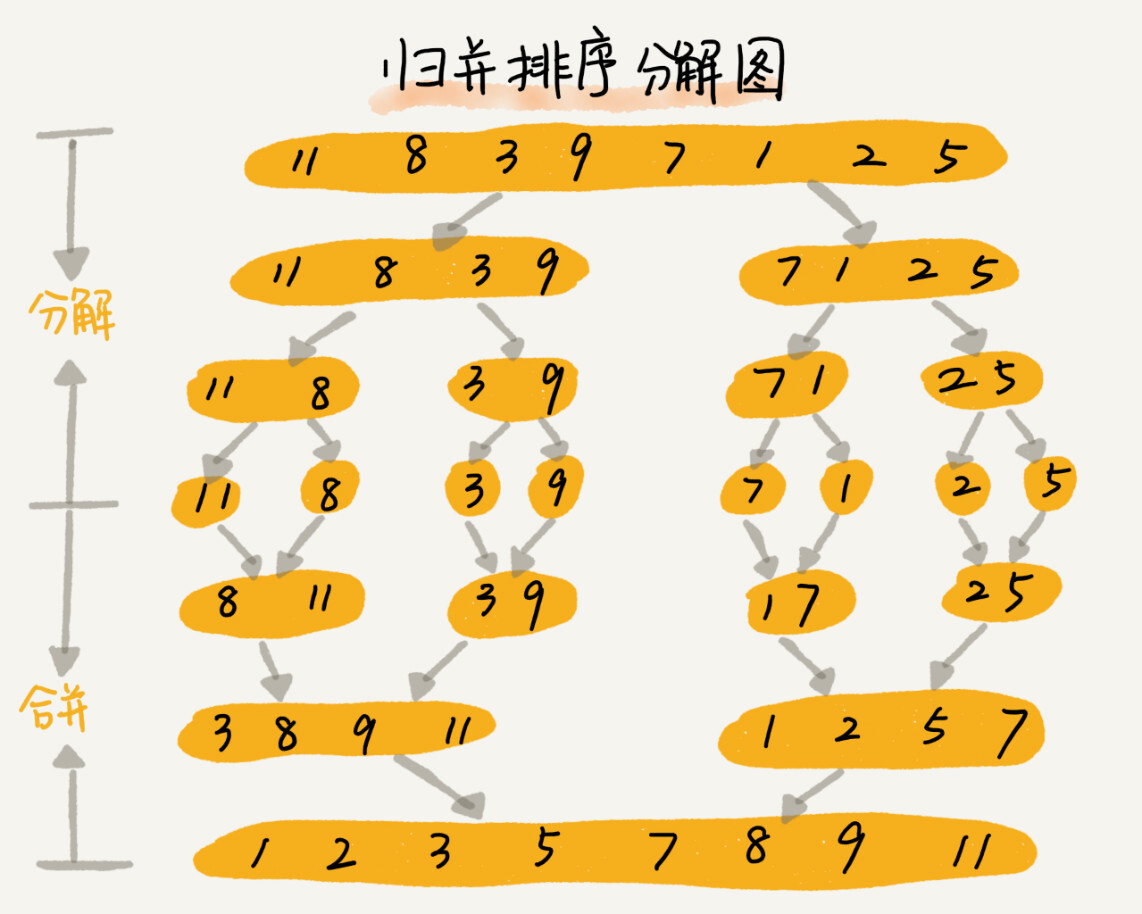
• 归并排序使用了「分治」思想（Divide and Conquer）
  • 分：把数组分成前后两部分，分别排序
  • 合：将有序的两部分合并

• 分治与递归
  • 分治：解决问题的处理办法
  • 递归：实现算法的手段
  • ——分治算法经常用递归来实现
• 递归实现：
  • 终止条件：区间 [first, last) 内不足 2 个元素
  • 递归公式：merge_sort(first, last) = merge(merge_sort(first, mid), merge_sort(mid, last))，其中 mid = first + (last - first) / 2

C++ 实现：

template <typename FrwdIt,
          typename T = typename std::iterator_traits<FrwdIt>::value_type,
          typename BinaryPred = std::less<T>>
void merge_sort(FrwdIt first, FrwdIt last, BinaryPred comp = BinaryPred()) {
    const auto len = std::distance(first, last);
    if (len <= 1) { return; }
    auto cut = first + len / 2;
    merge_sort(first, cut, comp);
    merge_sort(cut, last, comp);
    std::vector<T> tmp;
    tmp.reserve(len);
    detail::merge(first, cut, cut, last, std::back_inserter(tmp), comp);
    std::copy(tmp.begin(), tmp.end(), first);
}

这里涉及到一个 merge 的过程，它的实现大致是：

namespace detail {
template <typename InputIt1, typename InputIt2, typename OutputIt,
          typename BinaryPred = std::less<typename std::iterator_traits<InputIt1>::value_type>>
OutputIt merge(InputIt1 first1, InputIt1 last1,
               InputIt2 first2, InputIt2 last2,
               OutputIt d_first,
               BinaryPred comp = BinaryPred()) {
    for (; first1 != last1; ++d_first) {
        if (first2 == last2) {
            return std::copy(first1, last1, d_first);
        }
        if (comp(*first2, *first1)) {
            *d_first = *first2;
            ++first2;
        } else {
            *d_first = *first1;
            ++first1;
        }
    }
    return std::copy(first2, last2, d_first);
}
}  // namespace detail

算法分析

• 稳定性
  • 由于 comp 是严格偏序，所以 !comp(*first2, *first1) 时，取用 first1 的元素放入 d_first 保证了算法稳定性
• 时间复杂度
  • 定义 $T(n)$ 表示问题规模为 $n$ 时算法的耗时，
  • 有递推公式：$T(n) = 2T(n/2) + n$
  • 展开得 $T(n) = 2^{k}T(1) + k * n$
  • 考虑 $k$ 是递归深度，它的值是 $\log_2 n$，因此 $T(n) = n + n\log_2 n$
  • 因此，归并排序的时间复杂度为 $\Theta(n\log n)$
• 空间复杂度
  • 一般来说，空间复杂度是 $\Theta(n)$

快速排序（quick sort，快排）

原理：

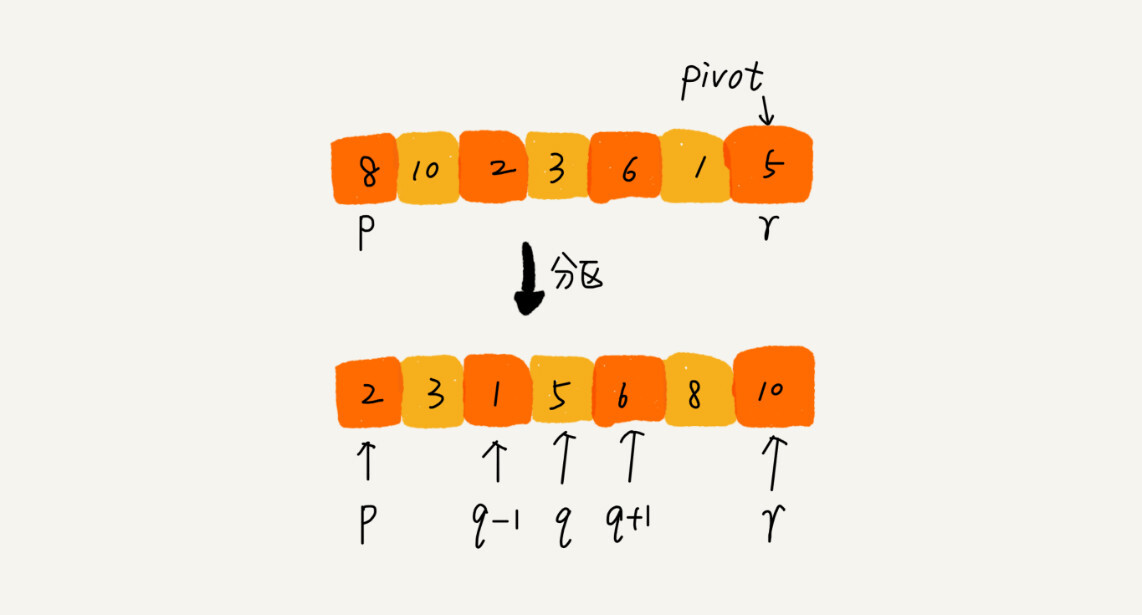
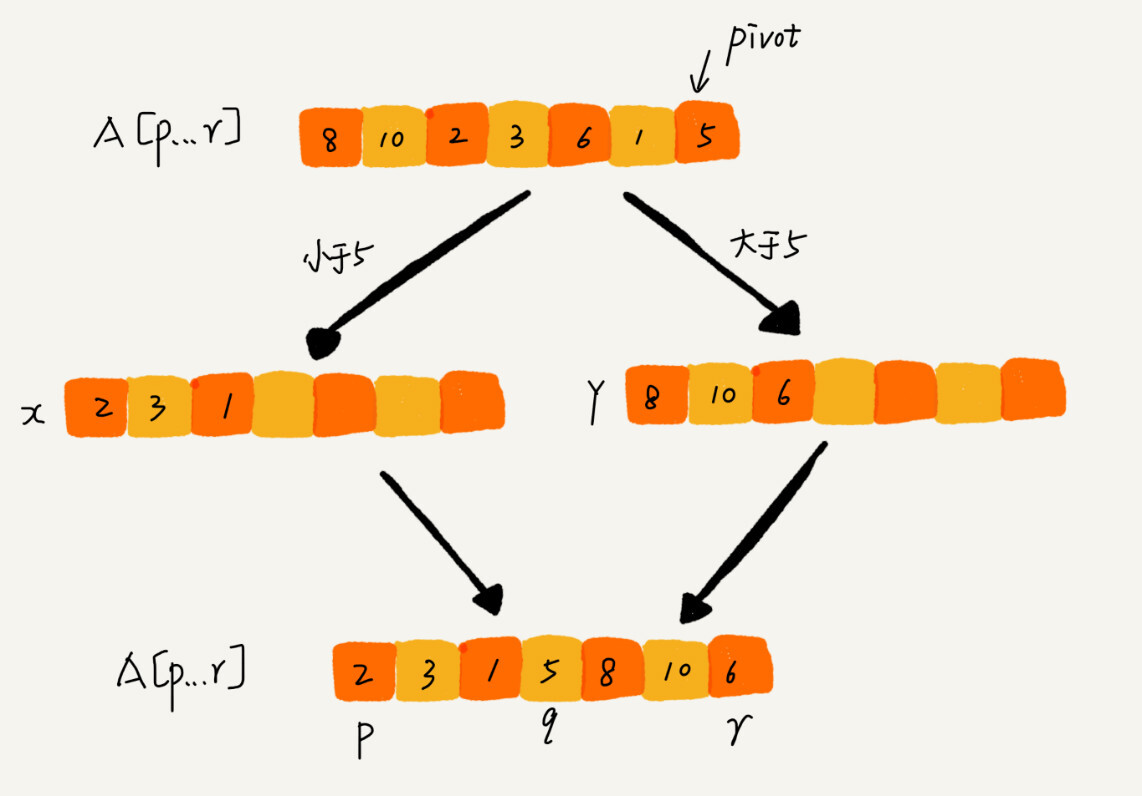
• 在待排序区间 [first, last) 中选取一个元素，称为主元（pivot，枢轴）
• 对待排序区间进行划分，使得 [first, cut) 中的元素满足 comp(element, pivot) 而 [cut, last) 中的元素不满足 comp(element, pivot)
• 对划分的两个区间，继续划分，直到区间 [first, last) 内不足 2 个元素

显然，这又是一个递归：

• 终止条件：区间 [first, last) 内不足 2 个元素
• 递归公式：quick_sort(first, last) = quick_sort(first, cut) + quick_sort(cut, last)

template <typename IterT, typename T = typename std::iterator_traits<IterT>::value_type>
void quick_sort(IterT first, IterT last) {
    if (std::distance(first, last) > 1) {
        IterT prev_last = std::prev(last);
        IterT cut = std::partition(first, prev_last, [prev_last](T v) { return v < *prev_last; });
        std::iter_swap(cut, prev_last);
        quick_sort(first, cut);
        quick_sort(cut, last);
    }
}

一点优化（Liam Huang）：通过将 if 改为 while 同时修改 last 迭代器的值，可以节省一半递归调用的开销。

template <typename IterT, typename T = typename std::iterator_traits<IterT>::value_type>
void quick_sort(IterT first, IterT last) {
    while (std::distance(first, last) > 1) {
        IterT prev_last = std::prev(last);
        IterT cut = std::partition(first, prev_last, [prev_last](T v) { return v < *prev_last; });
        std::iter_swap(cut, prev_last);
        quick_sort(cut, last);
        last = cut;
    }
}

如果不要求空间复杂度，分区函数实现起来很容易。

若要求原地分区，则不那么容易了。下面的实现实现了原地分区函数，并且能将所有相等的主元排在一起。

template <typename BidirIt,
          typename T = typename std::iterator_traits<BidirIt>::value_type,
          typename Compare = std::less<T>>
std::pair<BidirIt, BidirIt> inplace_partition(BidirIt first,
                                              BidirIt last,
                                             const T& pivot,
                                           Compare comp = Compare()) {
    BidirIt last_less, last_greater, first_equal, last_equal;
    for (last_less = first, last_greater = first, first_equal = last;
                                         last_greater != first_equal; ) {
        if (comp(*last_greater, pivot)) {
            std::iter_swap(last_greater++, last_less++);
        } else if (comp(pivot, *last_greater)) {
            ++last_greater;
        } else {  // pivot == *last_greater
            std::iter_swap(last_greater, --first_equal);
        }
    }
    const auto cnt = std::distance(first_equal, last);
    std::swap_ranges(first_equal, last, last_less);
    first_equal    = last_less;
    last_equal     = first_equal + cnt;
    return {first_equal, last_equal};
}

算法分析

• 稳定性
  • 由于 inplace_partition 使用了大量 std::iter_swap 操作，所以不是稳定排序
• 时间复杂度
  • 定义 $T(n)$ 表示问题规模为 $n$ 时算法的耗时，
  • 有递推公式：$T(n) = 2T(n/2) + n$（假定每次分割都是均衡分割）
  • 展开得 $T(n) = 2^{k}T(1) + k * n$
  • 考虑 $k$ 是递归深度，它的值是 $\log_2 n$，因此 $T(n) = n + n\log_2 n$
  • 因此，快速排序的时间复杂度为 $\Theta(n\log n)$
• 空间复杂度
  • 一般来说，空间复杂度是 $\Theta(1)$，因此是原地排序算法

开篇问题

• 分区，看前半段元素数量
  • 前半段元素数量 < K，对后半段进行分区
  • 前半段元素数量 > K，对前半段进行分区
  • 前半段元素数量 = K，前半段末位元素即是所求