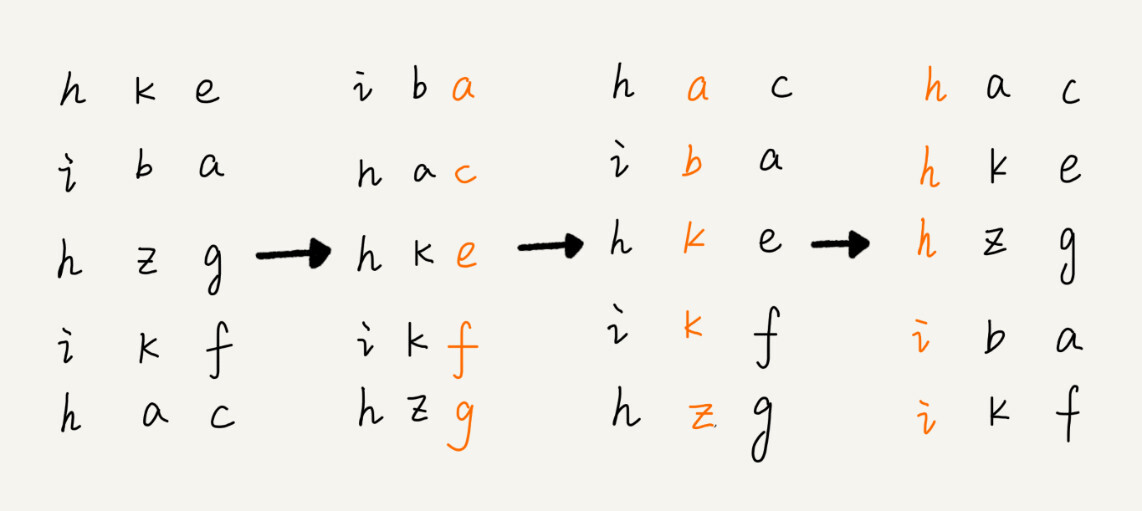如何按年龄给 100 万用户排序?
算法思想:
- 按待排序数据的 key 分有序桶
- 桶内排序
- 有序桶依次输出
- 时间复杂度
$O(n)$ -
$n$ 个元素,分$m$ 个有序桶,每个桶里平均$k = n / m$ 个元素 - 桶内快排,复杂度
$O(k \log k)$ ,$m$ 个桶一共$O(n \log k)$ - 当
$m$ 接近$n$ ,例如当$k = 4$ 时,这个复杂度近似$O(n)$
-
- 使用条件
- 数据易于分如有序桶
- 数据在各个有序桶之间分布均匀
- 适合外部排序——数据不全部载入磁盘
计数排序可以视作是桶排序的一个特殊情况:
- 数据的取值范围很小
- 每个分桶内的元素 key 值都一样
此时,由于分桶内的元素 key 值都一样,所以桶内的排序操作可以省略,以及桶的编号本身就能记录桶内元素的值。因此,算法只需遍历一遍所有的数据,统计每个取值上有多少元素即可。这个过程时间复杂度是
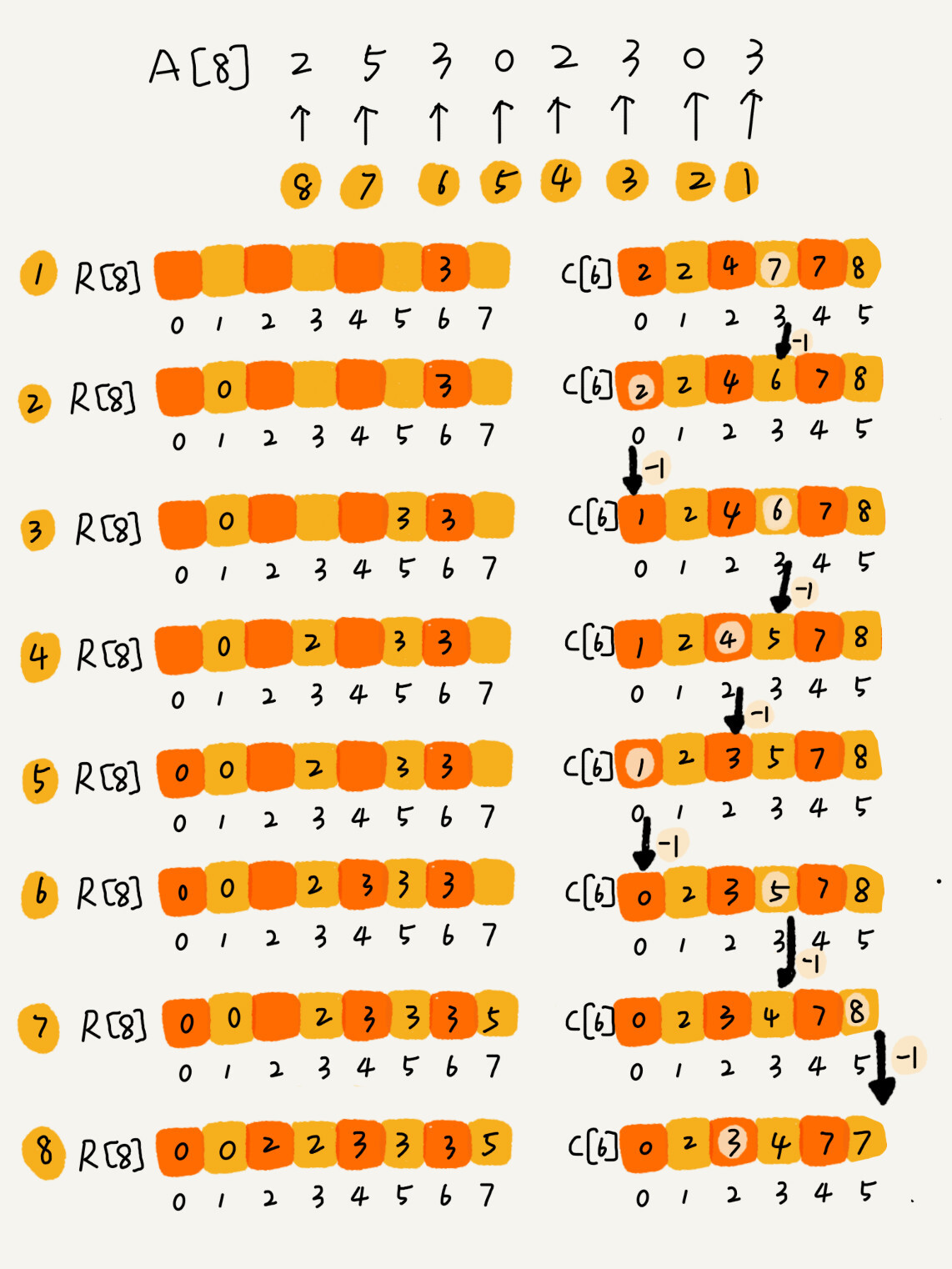
- 假设待排序的数组
A = {2, 5, 3, 0, 2, 3, 0, 3},我们有计数数组C = {2, 0, 2, 3, 0, 1}
接下来,我们要对 C 进行计数操作,具体来说,对从下标为 1 的元素开始累加 C[i] += C[i - 1]。
- 计数累加
C = {2, 2, 4, 7, 7, 8}
此时,C 中的元素表示「小于等于下标的元素的个数」。接下来,我们从尾至头扫描待排序数组 A,将其中元素依次拷贝到输出数组 R 的相应位置。我们注意到,A[7] = 3 而 C[3] == 4 。这意味着,待排序的数组中,包括 3 本身在内,不超过 3 的元素共有 4 个。因此,我们可以将这个 3 放置在 R[C[3] - 1] 的位置,而后将 C[3] 的计数减一——这是由于待排序数组中未处理的部分,不超过 3 的元素现在只剩下 3 个了。如此遍历整个待排序数组 A,即可得到排序后的结果 R。
- 时间复杂度
-
$n$ 个元素,最大值是$k$ ,分$k$ 个「桶」;时间复杂度$O(n)$ - 桶内计数累加;时间复杂度
$O(k)$ - 摆放元素;时间复杂度
$O(n)$ - 当
$k < n$ 时,总体时间复杂度是$O(n)$
-
- 使用条件
$k < n$ - 待排序数据的 key 是非负整数
基数排序适用于等长数据的排序。对于不等长数据,可以在较短的数据后面做 padding,使得数据等长。
- 先就 least significant digit 进行稳定排序——通常可以用桶排序或者计数排序;时间复杂度
$O(n)$ - 而后依次向 greatest significant digit 移动,进行稳定排序
- 时间复杂度
- 对每一位的排序时间复杂度是
$O(n)$ - 总共
$k$ 位,因此总的时间复杂度是$O(kn)$ ;考虑到$k$ 是常数,因此总的时间复杂度是$O(n)$
- 对每一位的排序时间复杂度是
- 使用条件
- 等长数据
桶排序。