Skip to content

Latest commit

 

History

History
227 lines (160 loc) · 4.05 KB

graphs.org

File metadata and controls

227 lines (160 loc) · 4.05 KB
Raw

Inductive Graphs

Graphs: Hard in Haskell?

Graph algorithms and data structures:

too imperative

Pattern match on a graph?

What can we match on?

  • lists
  • trees
  • algebraic data types

Why?

Algebraic data types are inductive:

there is exactly one way to construct them

Consider lists:

data List a = Nil | Cons a (List a)

one way to construct

Nil
Cons 1 (Cons 2 Nil)

one way to deconstruct

case list of
  Nil       -> ...
  Cons x xs -> ...

Graphs are not inductive

Graph construction — implementation detail

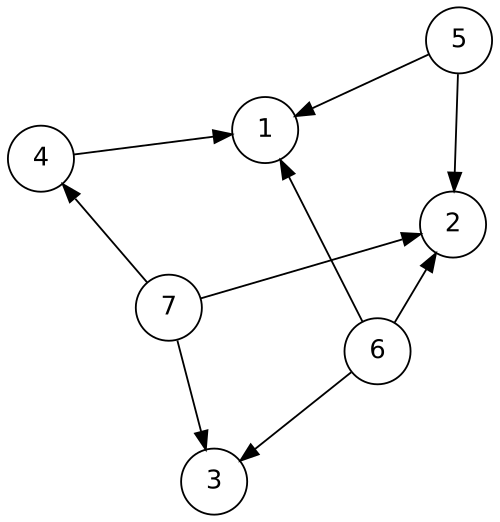
nodes are not ordered

Let’s pretend!

View graphs as inductive

Decompose into:

  • a node
  • its edges
  • the rest of the graph

View graphs as ADTs

data Context =
  Context [Node] Node [Node]

data View =
  Context :& Graph

(ignoring node and edge labels)

full.png

match1.png

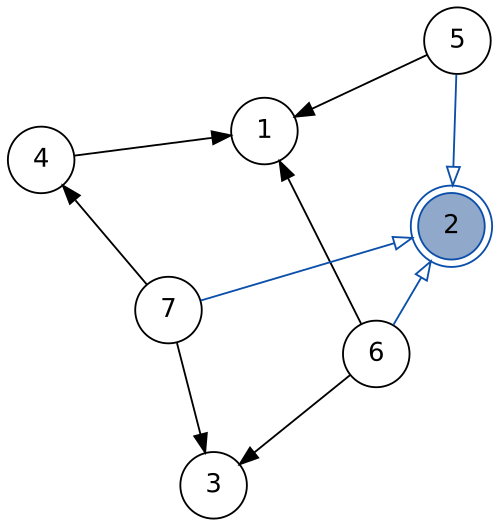
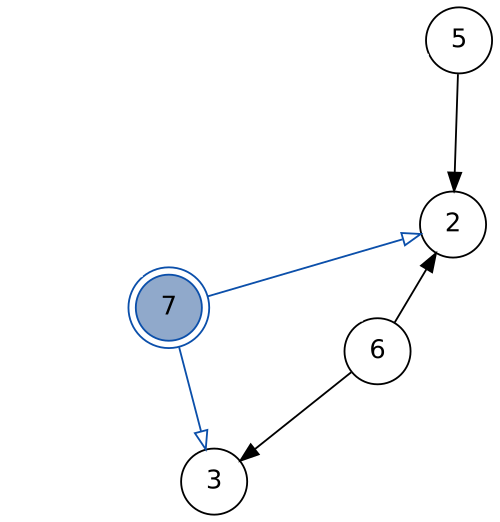
([4, 5, 6], 1, []) :& graph

recurse.png

the rest of the graph

Like lists:

match

list-match-cropped.png

recurse

list-recurse-cropped.png

Another match

match2.png

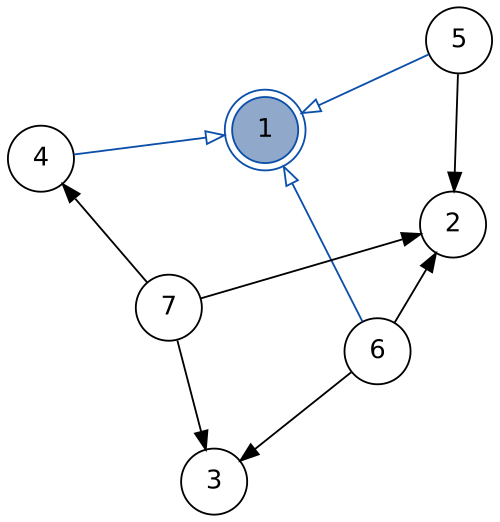
([5, 6, 7], 2, []) :& graph

matchAny

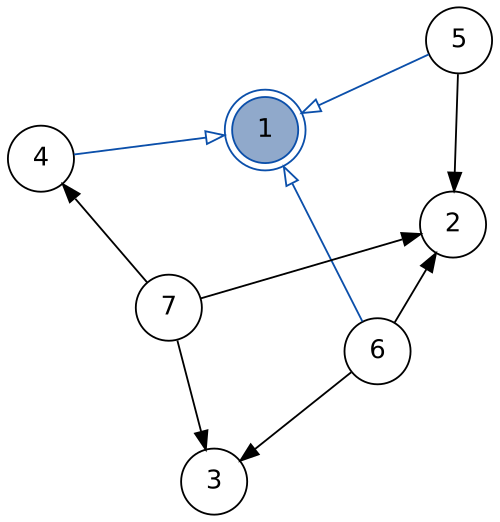
matchAny :: Graph -> View
foo :: Graph -> ...
foo graph | isEmpty graph     = ...
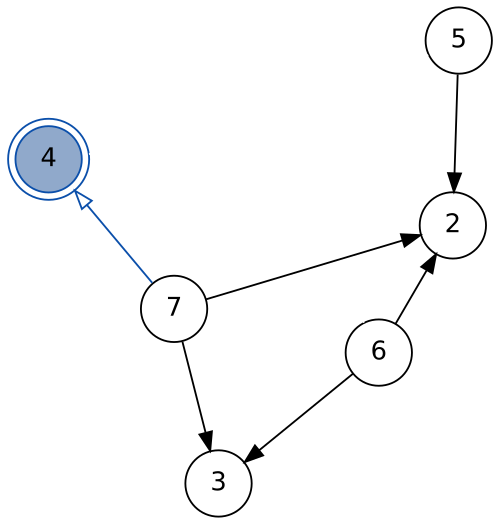
foo (matchAny -> ctx :& rest) = ...

match

match :: Node -> Graph -> Maybe View
  • matches a specific node
  • Nothing if not in graph
  • directed graph traversal

depth-first traversal

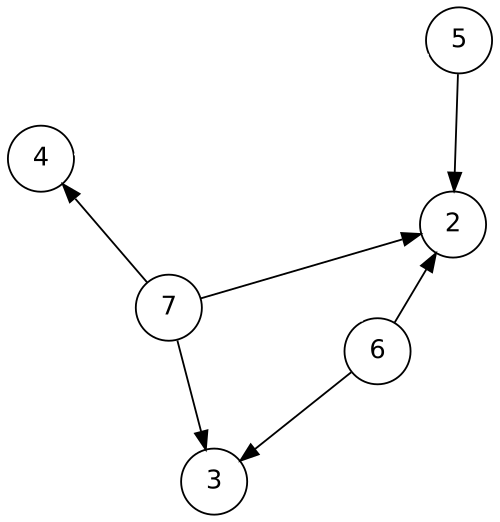
dfs :: [Node] -> Graph -> [Node]
dfs [] _ = []

dfs (x:xs) (match x -> Just (ctx :& g)) =
  x : dfs (neighbors ctx ++ xs) g

dfs (_:xs) graph = dfs xs graph

full.png

stack: []

result: []

step_0.png

stack: [4, 5, 6]

result: [1]

step_1.png

stack: [7, 5, 6]

result: [1, 4]

step_2.png

stack: [2, 3, 5, 6]

result: [1, 4, 7]

step_3.png

stack: [5, 6, 5, 6]

result: [1, 4, 7, 2]

step_4.png

stack: [6, 5, 6]

result: [1, 4, 7, 2, 5]

step_5.png

stack: [3, 5, 6]

result: [1, 4, 7, 2, 5, 6]

step_6.png

stack: [5, 6]

result: [1, 4, 7, 2, 5, 6, 3]

Pattern Matching on Graphs!

  • see graphs as inductive
  • use directed pattern matching
  • write normal functional code

Real World Use

  • fgl library
    • labels
    • directed edges
    • slightly different API
  • higher-order graph functions

Further Reading