1、关键点的提取与描述子的计算非常耗时。
实践当中,SIFT目前在CPU上是无法实时计算的,而ORB也需要近20毫秒的计算。
如果整个SLAM以30毫秒/帧的速度运行,那么一大半时间都花在计算特征点上。
2、使用特征点时,忽略了除特征点以外的所有信息。
一张图像有几十万个像素,而特征点只有几百个。
只使用特征点丢弃了大部分可能有用的图像信息。
3、相机有时会运动到特征缺失的地方,往往这些地方都没有什么明显的纹理信息。
例如,有时我们会面对一堵白墙,或者一个空荡荡的走廓。
这些场景下特征点数量会明显减少,我们可能找不到足够的匹配点来计算相机运动。
只计算关键点,不计算描述子。
同时,使用光流法(Optical Flow)来跟踪特征点的运动。
这样可以回避计算和匹配描述子带来的时间,但光流本身的计算需要一定时间;
仍然使用特征点,只是把匹配描述子替换成了光流跟踪,
估计相机运动时仍使用 RANSCK + PnP或ICP算法。
后面也可以使用BA进行优化。
只计算关键点,不计算描述子/计算关键点、也不计算描述子(梯度大小选择关键点)。
同时,使用直接法来计算特征点在下一时刻图像的位置。
这同样可以跳过描述子的计算过程,而且直接法的计算更加简单。
直接法估计相机运动,有已知的3d点,投影到两幅图像上,像素值应该没有变化(假设)
实际上会有误差,
ei=I1(p1,i)−I2(p2,i),
p1 = 1/z1*K*P
p2 = 1/z2*K*(R*P+t)
对误差e求优化变量的偏导数,可以得到优化变量的更新量。使用LM/GN算法优化
P 是一个已知位置的空间点,它是怎么来的呢?
在RGB-D相机下,我们使用深度信息可以把任意像素反投影到三维空间,然后投影到下一个图像中。
如果在单目相机中,我们也可以使用 一个估计的深度,来缺点特征点对应的3d点
(虽然是特征点(也可以是灰度梯度大的点),但直接法里是可以避免计算描述子的)。
根据P的来源,我们可以把直接法进行分类:
1、P来自于稀疏特征点,我们称之为稀疏直接法。
通常我们使用数百个特征点,并且会像L-K光流那样,假设它周围像素也是不变的。
这种稀疏直接法速度不必计算描述子,并且只使用数百个像素,因此速度最快,但只能计算稀疏的重构。
2、P来自部分像素。我们看到 对误差e求优化变量的偏导数 中,如果像素梯度为零,整一项雅可比就为零,
不会对计算运动增量有任何贡献。因此,可以考虑只使用带有梯度的像素点,舍弃像素梯度不明显的地方。
这称之为半稠密(Semi-Dense)的直接法,可以重构一个半稠密结构。
3、P为所有像素,称为稠密直接法。
稠密重构需要计算所有像素(一般几十万至几百万个),
因此多数不能在现有的 CPU上实时计算,需要GPU的加速。
相比于特征点法,直接法完全依靠像优化来求解相机位姿。

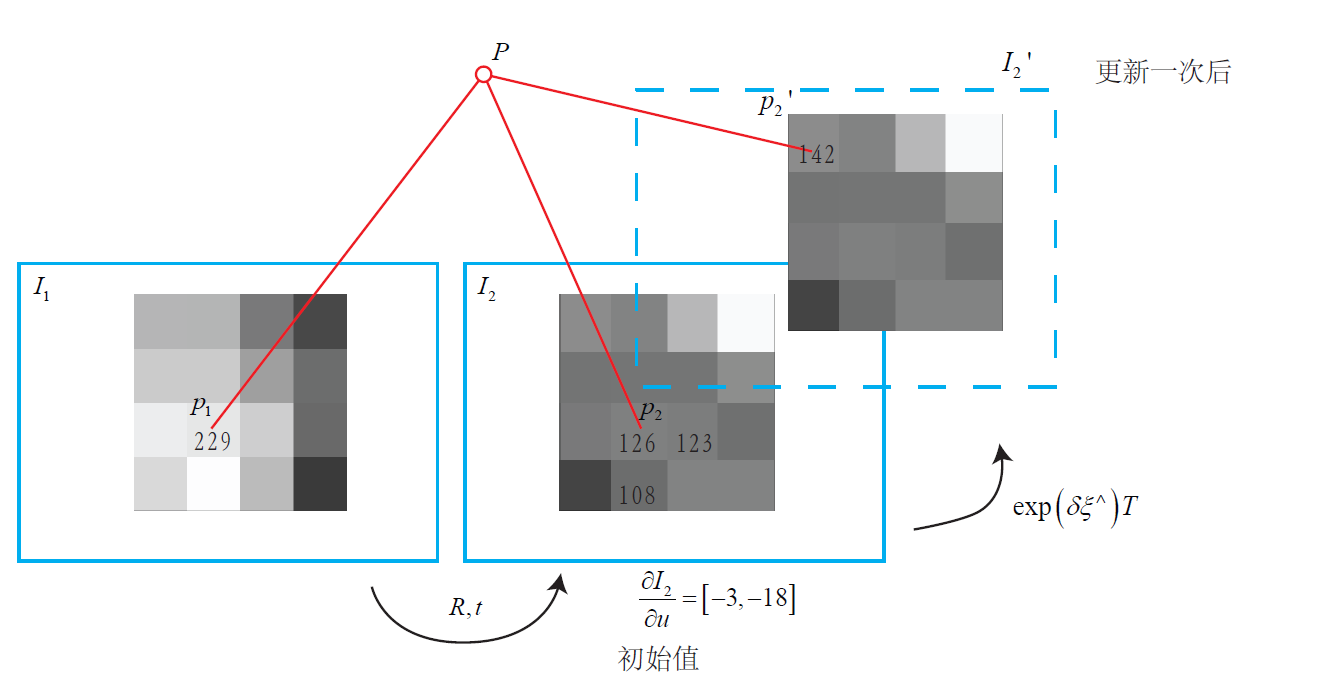
在帧1上 我们测量到一个灰度值为229的像素。
并且,我们知道它的深度(RGBD / 单目深度滤波得到),可以推断出空间点P的位置。
此时我们又得到了一张新的图像,需要估计它的相机位姿R,t。
这个位姿是由在一个初值上不断地优化迭代得到的。
假设我们的初值比较差,在这个初值下,空间点P投影到新的一帧上的像素灰度值是126。
于是,这个像素的误差为229−126=103,我们希望微调相机的位姿,使像素更亮一些。
怎么知道往哪里微调,像素会更亮呢?这就需要用到像素梯度。
我们在图像中发现,沿u轴往前走一步,该处的灰度值变成了123,即减去了3。
同样地,沿v轴往前走一步,灰度值减18,变成108。
在这个像素周围,我们看到梯度是[−3,−18],
为了提高亮度,我们会建议优化算法微调相机,使P的像往左上方移动。
由于这个梯度是在局部求解的,这个移动量不能太大。
但是,优化算法不能只听这个像素的一面之词,还需要听取其他像素的建议。
综合听取了许多像素的意见之后,优化算法选择了一个和我们建议的方向偏离不远的地方,
计算出一个更新量 exp(ξ)
对R,t左乘更新后 得到一个新的位姿,图像从I2移动到了I′2
像素的投影位置也变到了一个更亮的地方。我们看到,通过这次更新,误差变小了。
在理想情况下,我们期望误差会不断下降,最后收敛。
但是实际是不是这样呢?我们是否真的只要沿着梯度方向走,就能走到一个最优值?
注意到,直接法的梯度是直接由图像梯度确定的,
因此我们必须保证沿着图像梯度走时,灰度误差会不断下降。
然而,图像通常是一个很强烈的非凸函数,如下图所示。
实际当中,如果我们沿着图像梯度前进,
很容易由于图像本身的非凸性(或噪声)落进一个局部极小值中,无法继续优化。
只有当相机运动很小,图像中的梯度不会有很强的非凸性时,直接法才能成立。
在例程中,我们只计算了单个像素的差异,并且这个差异是由灰度直接相减得到的。
然而,单个像素没有什么区分性,周围很可能有好多像素和它的亮度差不多。
所以,我们有时会使用小的图像块(patch),并且使用更复杂的差异度量方式,
例如归一化相关性(Normalized Cross Correlation,NCC)/差平方和SSD/差绝对值和SAD 等。
而例程为了简单起见,使用了误差的平方和,以保持和推导的一致性。
大体来说,它的优点如下:
1、可以省去计算特征点、描述子的时间。
2、只要求有像素梯度即可,无须特征点。
因此,直接法可以在特征缺失的场合下使用。
比较极端的例子是只有渐变的一张图像。
它可能无法提取角点类特征,但可以用直接法估计它的运动。
3、可以构建半稠密乃至稠密的地图,这是特征点法无法做到的。
另一方面,它的缺点也很明显:
1、非凸性。
直接法完全依靠梯度搜索,降低目标函数来计算相机位姿。
其目标函数中需要取像素点的灰度值,而图像是强烈非凸的函数。
这使得优化算法容易进入极小,只在运动很小时直接法才能成功。
2、单个像素没有区分度。
找一个和他像的实在太多了!——于是我们要么计算图像块,要么计算复杂的相关性。
由于每个像素对改变相机运动的“意见”不一致。
只能少数服从多数,以数量代替质量。
3、灰度值不变是很强的假设。
如果相机是自动曝光的,当它调整曝光参数时,会使得图像整体变亮或变暗。
光照变化时亦会出现这种情况。
特征点法对光照具有一定的容忍性,而直接法由于计算灰度间的差异,
整体灰度变化会破坏灰度不变假设,使算法失败。