Zipline is an open-source algorithmic trading simulator written in Python.
The source can be found at: https://github.com/quantopian/zipline
Some benefits include:
- Realistic: slippage, transaction costs, order delays.
- Stream-based: Process each event individually, avoids look-ahead bias.
- Batteries included: Common transforms (moving average) as well as common risk calculations (Sharpe).
- Developed and continuously updated by Quantopian which provides an easy-to-use web-interface to Zipline, 10 years of minute-resolution historical US stock data, and live-trading capabilities. This tutorial is directed at users wishing to use Zipline without using Quantopian. If you instead want to get started on Quantopian, see here.
This tutorial assumes that you have zipline correctly installed, see the installation instructions if you haven't set up zipline yet.
Every zipline algorithm consists of two functions you have to
define:
initialize(context)handle_data(context, data)
Before the start of the algorithm, zipline calls the
initialize() function and passes in a context variable.
context is a persistent namespace for you to store variables you
need to access from one algorithm iteration to the next.
After the algorithm has been initialized, zipline calls the
handle_data() function once for each event. At every call, it passes
the same context variable and an event-frame called data
containing the current trading bar with open, high, low, and close
(OHLC) prices as well as volume for each stock in your universe. For
more information on these functions, see the relevant part of the
Quantopian docs.
Lets take a look at a very simple algorithm from the examples
directory, buyapple.py:
from zipline.examples import buyapple
buyapple??from zipline.api import order, record, symbol
def initialize(context):
pass
def handle_data(context, data):
order(symbol('AAPL'), 10)
record(AAPL=data.current(symbol('AAPL'), 'price'))As you can see, we first have to import some functions we would like to
use. All functions commonly used in your algorithm can be found in
zipline.api. Here we are using :func:`~zipline.api.order()` which takes two
arguments: a security object, and a number specifying how many stocks you would
like to order (if negative, :func:`~zipline.api.order()` will sell/short
stocks). In this case we want to order 10 shares of Apple at each iteration. For
more documentation on order(), see the Quantopian docs.
Finally, the :func:`~zipline.api.record` function allows you to save the value
of a variable at each iteration. You provide it with a name for the variable
together with the variable itself: varname=var. After the algorithm
finished running you will have access to each variable value you tracked
with :func:`~zipline.api.record` under the name you provided (we will see this
further below). You also see how we can access the current price data of the
AAPL stock in the data event frame (for more information see
here.
To now test this algorithm on financial data, zipline provides three
interfaces: A command-line interface, IPython Notebook magic, and
:func:`~zipline.run_algorithm`.
If you haven't ingested the data, run:
$ zipline ingest [-b <bundle>]where <bundle> is the name of the bundle to ingest, defaulting to
:ref:`quantopian-quandl <quantopian-quandl-mirror>`.
you can check out the :ref:`ingesting data <ingesting-data>` section for more detail.
After you installed zipline you should be able to execute the following
from your command line (e.g. cmd.exe on Windows, or the Terminal app
on OSX):
$ zipline run --helpUsage: zipline run [OPTIONS]
Run a backtest for the given algorithm.
Options:
-f, --algofile FILENAME The file that contains the algorithm to run.
-t, --algotext TEXT The algorithm script to run.
-D, --define TEXT Define a name to be bound in the namespace
before executing the algotext. For example
'-Dname=value'. The value may be any python
expression. These are evaluated in order so
they may refer to previously defined names.
--data-frequency [minute|daily]
The data frequency of the simulation.
[default: daily]
--capital-base FLOAT The starting capital for the simulation.
[default: 10000000.0]
-b, --bundle BUNDLE-NAME The data bundle to use for the simulation.
[default: quantopian-quandl]
--bundle-timestamp TIMESTAMP The date to lookup data on or before.
[default: <current-time>]
-s, --start DATE The start date of the simulation.
-e, --end DATE The end date of the simulation.
-o, --output FILENAME The location to write the perf data. If this
is '-' the perf will be written to stdout.
[default: -]
--print-algo / --no-print-algo Print the algorithm to stdout.
--help Show this message and exit.
As you can see there are a couple of flags that specify where to find your
algorithm (-f) as well as parameters specifying which data to use,
defaulting to the :ref:`quantopian-quandl-mirror`. There are also arguments for
the date range to run the algorithm over (--start and --end). Finally,
you'll want to save the performance metrics of your algorithm so that you can
analyze how it performed. This is done via the --output flag and will cause
it to write the performance DataFrame in the pickle Python file format.
Note that you can also define a configuration file with these parameters that
you can then conveniently pass to the -c option so that you don't have to
supply the command line args all the time (see the .conf files in the examples
directory).
Thus, to execute our algorithm from above and save the results to
buyapple_out.pickle we would call zipline run as follows:
zipline run -f ../../zipline/examples/buyapple.py --start 2000-1-1 --end 2014-1-1 -o buyapple_out.pickleAAPL [2015-11-04 22:45:32.820166] INFO: Performance: Simulated 3521 trading days out of 3521. [2015-11-04 22:45:32.820314] INFO: Performance: first open: 2000-01-03 14:31:00+00:00 [2015-11-04 22:45:32.820401] INFO: Performance: last close: 2013-12-31 21:00:00+00:00
run first calls the initialize() function, and then
streams the historical stock price day-by-day through handle_data().
After each call to handle_data() we instruct zipline to order 10
stocks of AAPL. After the call of the order() function, zipline
enters the ordered stock and amount in the order book. After the
handle_data() function has finished, zipline looks for any open
orders and tries to fill them. If the trading volume is high enough for
this stock, the order is executed after adding the commission and
applying the slippage model which models the influence of your order on
the stock price, so your algorithm will be charged more than just the
stock price * 10. (Note, that you can also change the commission and
slippage model that zipline uses, see the Quantopian
docs for more
information).
Lets take a quick look at the performance DataFrame. For this, we
use pandas from inside the IPython Notebook and print the first ten
rows. Note that zipline makes heavy usage of pandas, especially
for data input and outputting so it's worth spending some time to learn
it.
import pandas as pd
perf = pd.read_pickle('buyapple_out.pickle') # read in perf DataFrame
perf.head()| AAPL | algo_volatility | algorithm_period_return | alpha | benchmark_period_return | benchmark_volatility | beta | capital_used | ending_cash | ending_exposure | ... | short_exposure | short_value | shorts_count | sortino | starting_cash | starting_exposure | starting_value | trading_days | transactions | treasury_period_return | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000-01-03 21:00:00 | 3.738314 | 0.000000e+00 | 0.000000e+00 | -0.065800 | -0.009549 | 0.000000 | 0.000000 | 0.00000 | 10000000.00000 | 0.00000 | ... | 0 | 0 | 0 | 0.000000 | 10000000.00000 | 0.00000 | 0.00000 | 1 | [] | 0.0658 |
| 2000-01-04 21:00:00 | 3.423135 | 3.367492e-07 | -3.000000e-08 | -0.064897 | -0.047528 | 0.323229 | 0.000001 | -34.53135 | 9999965.46865 | 34.23135 | ... | 0 | 0 | 0 | 0.000000 | 10000000.00000 | 0.00000 | 0.00000 | 2 | [{u'order_id': u'513357725cb64a539e3dd02b47da7... | 0.0649 |
| 2000-01-05 21:00:00 | 3.473229 | 4.001918e-07 | -9.906000e-09 | -0.066196 | -0.045697 | 0.329321 | 0.000001 | -35.03229 | 9999930.43636 | 69.46458 | ... | 0 | 0 | 0 | 0.000000 | 9999965.46865 | 34.23135 | 34.23135 | 3 | [{u'order_id': u'd7d4ad03cfec4d578c0d817dc3829... | 0.0662 |
| 2000-01-06 21:00:00 | 3.172661 | 4.993979e-06 | -6.410420e-07 | -0.065758 | -0.044785 | 0.298325 | -0.000006 | -32.02661 | 9999898.40975 | 95.17983 | ... | 0 | 0 | 0 | -12731.780516 | 9999930.43636 | 69.46458 | 69.46458 | 4 | [{u'order_id': u'1fbf5e9bfd7c4d9cb2e8383e1085e... | 0.0657 |
| 2000-01-07 21:00:00 | 3.322945 | 5.977002e-06 | -2.201900e-07 | -0.065206 | -0.018908 | 0.375301 | 0.000005 | -33.52945 | 9999864.88030 | 132.91780 | ... | 0 | 0 | 0 | -12629.274583 | 9999898.40975 | 95.17983 | 95.17983 | 5 | [{u'order_id': u'9ea6b142ff09466b9113331a37437... | 0.0652 |
5 rows × 39 columns
As you can see, there is a row for each trading day, starting on the
first business day of 2000. In the columns you can find various
information about the state of your algorithm. The very first column
AAPL was placed there by the record() function mentioned earlier
and allows us to plot the price of apple. For example, we could easily
examine now how our portfolio value changed over time compared to the
AAPL stock price.
%pylab inline
figsize(12, 12)
import matplotlib.pyplot as plt
ax1 = plt.subplot(211)
perf.portfolio_value.plot(ax=ax1)
ax1.set_ylabel('portfolio value')
ax2 = plt.subplot(212, sharex=ax1)
perf.AAPL.plot(ax=ax2)
ax2.set_ylabel('AAPL stock price')Populating the interactive namespace from numpy and matplotlib
<matplotlib.text.Text at 0x7ff5c6147f90>
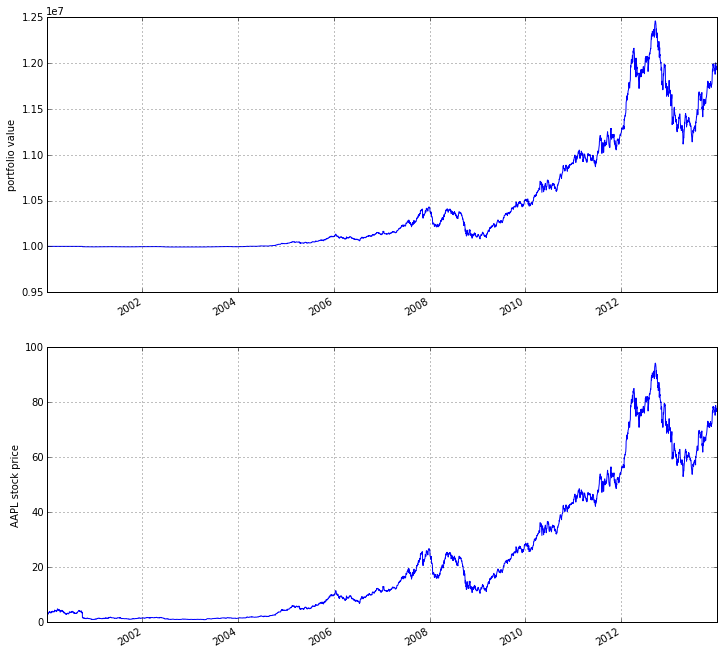
As you can see, our algorithm performance as assessed by the
portfolio_value closely matches that of the AAPL stock price. This
is not surprising as our algorithm only bought AAPL every chance it got.
The IPython Notebook is a very
powerful browser-based interface to a Python interpreter (this tutorial
was written in it). As it is already the de-facto interface for most
quantitative researchers zipline provides an easy way to run your
algorithm inside the Notebook without requiring you to use the CLI.
To use it you have to write your algorithm in a cell and let zipline
know that it is supposed to run this algorithm. This is done via the
%%zipline IPython magic command that is available after you
import zipline from within the IPython Notebook. This magic takes
the same arguments as the command line interface described above. Thus
to run the algorithm from above with the same parameters we just have to
execute the following cell after importing zipline to register the
magic.
%load_ext zipline%%zipline --start 2000-1-1 --end 2014-1-1
from zipline.api import symbol, order, record
def initialize(context):
pass
def handle_data(context, data):
order(symbol('AAPL'), 10)
record(AAPL=data[symbol('AAPL')].price)Note that we did not have to specify an input file as above since the
magic will use the contents of the cell and look for your algorithm
functions there. Also, instead of defining an output file we are
specifying a variable name with -o that will be created in the name
space and contain the performance DataFrame we looked at above.
_.head()| AAPL | algo_volatility | algorithm_period_return | alpha | benchmark_period_return | benchmark_volatility | beta | capital_used | ending_cash | ending_exposure | ... | short_exposure | short_value | shorts_count | sortino | starting_cash | starting_exposure | starting_value | trading_days | transactions | treasury_period_return | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000-01-03 21:00:00 | 3.738314 | 0.000000e+00 | 0.000000e+00 | -0.065800 | -0.009549 | 0.000000 | 0.000000 | 0.00000 | 10000000.00000 | 0.00000 | ... | 0 | 0 | 0 | 0.000000 | 10000000.00000 | 0.00000 | 0.00000 | 1 | [] | 0.0658 |
| 2000-01-04 21:00:00 | 3.423135 | 3.367492e-07 | -3.000000e-08 | -0.064897 | -0.047528 | 0.323229 | 0.000001 | -34.53135 | 9999965.46865 | 34.23135 | ... | 0 | 0 | 0 | 0.000000 | 10000000.00000 | 0.00000 | 0.00000 | 2 | [{u'commission': 0.3, u'amount': 10, u'sid': 0... | 0.0649 |
| 2000-01-05 21:00:00 | 3.473229 | 4.001918e-07 | -9.906000e-09 | -0.066196 | -0.045697 | 0.329321 | 0.000001 | -35.03229 | 9999930.43636 | 69.46458 | ... | 0 | 0 | 0 | 0.000000 | 9999965.46865 | 34.23135 | 34.23135 | 3 | [{u'commission': 0.3, u'amount': 10, u'sid': 0... | 0.0662 |
| 2000-01-06 21:00:00 | 3.172661 | 4.993979e-06 | -6.410420e-07 | -0.065758 | -0.044785 | 0.298325 | -0.000006 | -32.02661 | 9999898.40975 | 95.17983 | ... | 0 | 0 | 0 | -12731.780516 | 9999930.43636 | 69.46458 | 69.46458 | 4 | [{u'commission': 0.3, u'amount': 10, u'sid': 0... | 0.0657 |
| 2000-01-07 21:00:00 | 3.322945 | 5.977002e-06 | -2.201900e-07 | -0.065206 | -0.018908 | 0.375301 | 0.000005 | -33.52945 | 9999864.88030 | 132.91780 | ... | 0 | 0 | 0 | -12629.274583 | 9999898.40975 | 95.17983 | 95.17983 | 5 | [{u'commission': 0.3, u'amount': 10, u'sid': 0... | 0.0652 |
5 rows × 39 columns
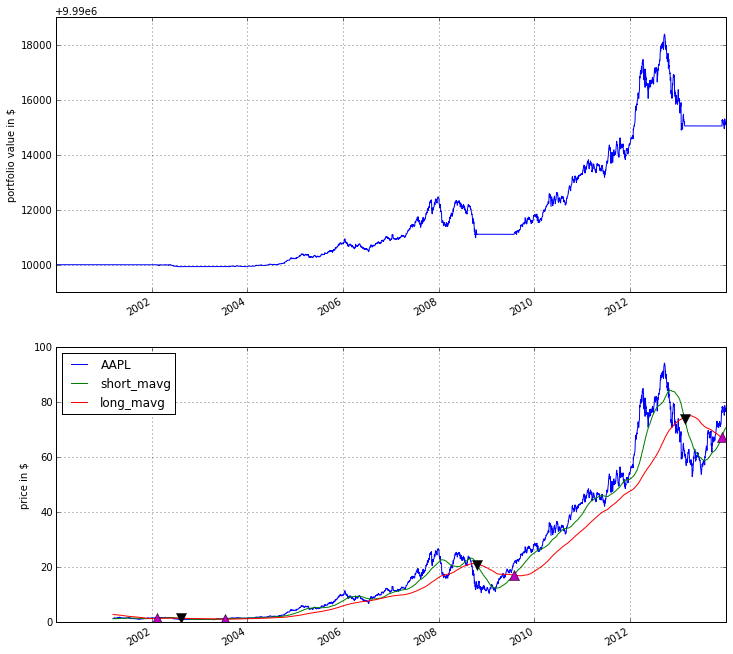
The Dual Moving Average (DMA) is a classic momentum strategy. It's probably not used by any serious trader anymore but is still very instructive. The basic idea is that we compute two rolling or moving averages (mavg) -- one with a longer window that is supposed to capture long-term trends and one shorter window that is supposed to capture short-term trends. Once the short-mavg crosses the long-mavg from below we assume that the stock price has upwards momentum and long the stock. If the short-mavg crosses from above we exit the positions as we assume the stock to go down further.
As we need to have access to previous prices to implement this strategy we need a new concept: History
data.history() is a convenience function that keeps a rolling window of
data for you. The first argument is the number of bars you want to
collect, the second argument is the unit (either '1d' for '1m'
but note that you need to have minute-level data for using 1m). For
a more detailed description history()'s features, see the
Quantopian docs.
Let's look at the strategy which should make this clear:
%%zipline --start 2000-1-1 --end 2012-1-1 -o dma.pickle
from zipline.api import order_target, record, symbol
def initialize(context):
context.i = 0
context.asset = symbol('AAPL')
def handle_data(context, data):
# Skip first 300 days to get full windows
context.i += 1
if context.i < 300:
return
# Compute averages
# data.history() has to be called with the same params
# from above and returns a pandas dataframe.
short_mavg = data.history(context.asset, 'price', bar_count=100, frequency="1d").mean()
long_mavg = data.history(context.asset, 'price', bar_count=300, frequency="1d").mean()
# Trading logic
if short_mavg > long_mavg:
# order_target orders as many shares as needed to
# achieve the desired number of shares.
order_target(context.asset, 100)
elif short_mavg < long_mavg:
order_target(context.asset, 0)
# Save values for later inspection
record(AAPL=data.current(context.asset, 'price'),
short_mavg=short_mavg,
long_mavg=long_mavg)
def analyze(context, perf):
fig = plt.figure()
ax1 = fig.add_subplot(211)
perf.portfolio_value.plot(ax=ax1)
ax1.set_ylabel('portfolio value in $')
ax2 = fig.add_subplot(212)
perf['AAPL'].plot(ax=ax2)
perf[['short_mavg', 'long_mavg']].plot(ax=ax2)
perf_trans = perf.ix[[t != [] for t in perf.transactions]]
buys = perf_trans.ix[[t[0]['amount'] > 0 for t in perf_trans.transactions]]
sells = perf_trans.ix[
[t[0]['amount'] < 0 for t in perf_trans.transactions]]
ax2.plot(buys.index, perf.short_mavg.ix[buys.index],
'^', markersize=10, color='m')
ax2.plot(sells.index, perf.short_mavg.ix[sells.index],
'v', markersize=10, color='k')
ax2.set_ylabel('price in $')
plt.legend(loc=0)
plt.show()Here we are explicitly defining an analyze() function that gets
automatically called once the backtest is done (this is not possible on
Quantopian currently).
Although it might not be directly apparent, the power of history()
(pun intended) can not be under-estimated as most algorithms make use of
prior market developments in one form or another. You could easily
devise a strategy that trains a classifier with
scikit-learn which tries to
predict future market movements based on past prices (note, that most of
the scikit-learn functions require numpy.ndarrays rather than
pandas.DataFrames, so you can simply pass the underlying
ndarray of a DataFrame via .values).
We also used the order_target() function above. This and other
functions like it can make order management and portfolio rebalancing
much easier. See the Quantopian documentation on order
functions fore
more details.
We hope that this tutorial gave you a little insight into the
architecture, API, and features of zipline. For next steps, check
out some of the
examples.
Feel free to ask questions on our mailing list, report problems on our GitHub issue tracker, get involved, and checkout Quantopian.