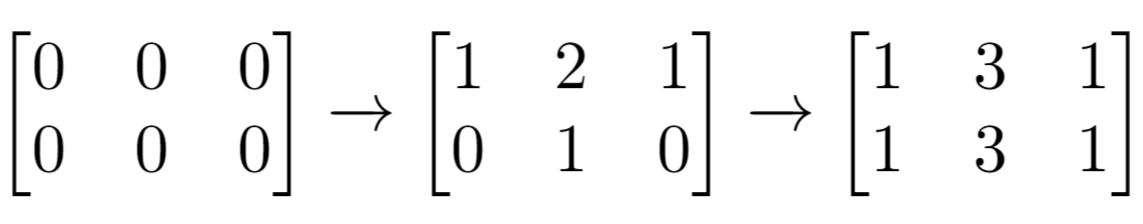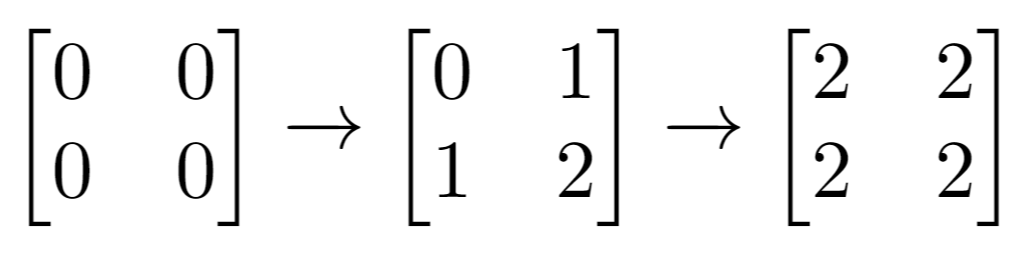1252. Cells with Odd Values in a Matrix

题目

Given n and m which are the dimensions of a matrix initialized by zeros and given an array indices where indices[i] = [ri, ci]. For each pair of [ri, ci] you have to increment all cells in row ri and column ci by 1.

Return the number of cells with odd values in the matrix after applying the increment to all indices.

Example 1:

Input: n = 2, m = 3, indices = [[0,1],[1,1]]
Output: 6
Explanation: Initial matrix = [[0,0,0],[0,0,0]].
After applying first increment it becomes [[1,2,1],[0,1,0]].
The final matrix will be [[1,3,1],[1,3,1]] which contains 6 odd numbers.

Example 2:

Input: n = 2, m = 2, indices = [[1,1],[0,0]]
Output: 0
Explanation: Final matrix = [[2,2],[2,2]]. There is no odd number in the final matrix.

Constraints:

• 1 <= n <= 50
• 1 <= m <= 50
• 1 <= indices.length <= 100
• 0 <= indices[i][0] < n
• 0 <= indices[i][1] < m

题目大意

给你一个 n 行 m 列的矩阵，最开始的时候，每个单元格中的值都是 0。另有一个索引数组 indices，indices[i] = [ri, ci] 中的 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。你需要将每对 [ri, ci] 指定的行和列上的所有单元格的值加 1。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 「奇数值单元格」 的数目。

提示：

• 1 <= n <= 50
• 1 <= m <= 50
• 1 <= indices.length <= 100
• 0 <= indices[i][0] < n
• 0 <= indices[i][1] < m

解题思路

• 给出一个 n * m 的矩阵，和一个数组，数组里面包含一些行列坐标，并在指定坐标上 + 1，问最后 n * m 的矩阵中奇数的总数。
• 暴力方法按照题意模拟即可。

代码

package leetcode

// 解法一 暴力法
func oddCells(n int, m int, indices [][]int) int {
	matrix, res := make([][]int, n), 0
	for i := range matrix {
		matrix[i] = make([]int, m)
	}
	for _, indice := range indices {
		for i := 0; i < m; i++ {
			matrix[indice[0]][i]++
		}
		for j := 0; j < n; j++ {
			matrix[j][indice[1]]++
		}
	}
	for _, m := range matrix {
		for _, v := range m {
			if v&1 == 1 {
				res++
			}
		}
	}
	return res
}

// 解法二 暴力法
func oddCells1(n int, m int, indices [][]int) int {
	rows, cols, count := make([]int, n), make([]int, m), 0
	for _, pair := range indices {
		rows[pair[0]]++
		cols[pair[1]]++
	}
	for i := 0; i < n; i++ {
		for j := 0; j < m; j++ {
			if (rows[i]+cols[j])%2 == 1 {
				count++
			}
		}
	}
	return count
}