Bitonic Sort is an efficient sorting algorithm based on the bitonic sequence concept and is often used in parallel processing due to its regular and repetitive structure. It works by first sorting sub-arrays in different directions and then combining them in a special merging process, ensuring a fully sorted array. This algorithm is particularly efficient when dealing with data sets whose size is a power of two.
- Parallel Processing: Bitonic sort is highly parallelizable, making it suitable for multi-threading and distributed systems, a strength that Rust can capitalize on with its robust concurrency features.
- Recursive Strategy: The algorithm uses recursive division of the array, which is elegantly handled in Rust with its strong support for recursion and memory safety.
- Efficiency: For medium-sized arrays, especially in parallel computing environments, bitonic sort can be very efficient, leveraging Rust's performance capabilities.
Properties
- Special Case Input: Bitonic sort is most efficient when the input size is a power of two.
- Time Complexity: In the worst-case scenario, the time complexity of bitonic sort is O(n log² n).
- Not-in-place Sorting: While it doesn't sort in place, it requires less extra space compared to other non-in-place sorting algorithms.
Sources to read:
From Wikipedia: In computer science, bogosort (also known as permutation sort, stupid sort, slowsort or bozosort) is a sorting algorithm based on the generate and test paradigm. The function successively generates permutations of its input until it finds one that is sorted. It is not considered useful for sorting, but may be used for educational purposes, to contrast it with more efficient algorithms.
Two versions of this algorithm exist: a deterministic version that enumerates all permutations until it hits a sorted one,and a randomized version that randomly permutes its input. An analogy for the working of the latter version is to sort a deck of cards by throwing the deck into the air, picking the cards up at random, and repeating the process until the deck is sorted. Its name is a portmanteau of the words bogus and sort.
From [leonardini.dev][bogo-bogo-doc]: BogoBogo Sort is a humorously inefficient sorting algorithm inspired by the original Bogosort. It adds a layer of complexity by recursively sorting the first n-1 elements before placing the nth element. This process is repeated until the array is sorted. The algorithm's performance is exceptionally poor, making it impractical for sorting but a useful tool for educational purposes, especially in understanding algorithm efficiency and recursive functions. Properties
- Worst case performance (unbounded, extremely poor)
- Best case performance O(n!)
- Average case performance (unpredictable and impractical)
From Wikipedia: Bucket sort, or bin sort, is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, a generalization of pigeonhole sort that allows multiple keys per bucket, and is a cousin of radix sort in the most-to-least significant digit flavor. Bucket sort can be implemented with comparisons and therefore can also be considered a comparison sort algorithm. The computational complexity depends on the algorithm used to sort each bucket, the number of buckets to use, and whether the input is uniformly distributed.
Bucket sort works as follows:
Set up an array of initially empty "buckets". Scatter: Go over the original array, putting each object in its bucket. Sort each non-empty bucket. Gather: Visit the buckets in order and put all elements back into the original array.
Optimization: A common optimization is to put the unsorted elements of the buckets back in the original array first, then run insertion sort over the complete array; because insertion sort's runtime is based on how far each element is from its final position, the number of comparisons remains relatively small, and the memory hierarchy is better exploited by storing the list contiguously in memory.
If the input distribution is known or can be estimated, buckets can often be chosen which contain constant density (rather than merely having constant size). This allows O(n) average time complexity even without uniformly distributed input.
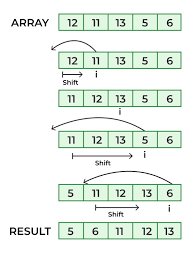
Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order.
- First Iteration (Compare and Swap)
- Starting from the first index, compare the first and the second elements.
- If the first element is greater than the second element, they are swapped.
- Now, compare the second and the third elements. Swap them if they are not in order.
- The above process goes on until the last element.
- Remaining Iteration
- The same process goes on for the remaining iterations.
- After each iteration, the largest element among the unsorted elements is placed at the end.
- In each iteration, the comparison takes place up to the last unsorted element.
- The array is sorted when all the unsorted elements are placed at their correct positions.
Properties
- Worst/Average time complexity : O(N2).
- This algorithm is not suitable for large data sets.
Sources to read:
Cocktail Shaker Sort, also called bidirectional bubble sort, iterates through a list from top to bottom and then from bottom to top. It is highly performant when the items in the list are partially sorted. The complexity of any list is O(n^2), but it approaches O(n) if the distance of each item from its final position in the ordered list is relatively small.
Sources to read:
Comb Sort is another optimization of Bubble Sort, and achieves this by eliminating small values towards the end of the list. It also uses a shrink-factor (k), which is used in the inner loop of Bubble Sort that performs the swapping of elements. The gap between elements that are compared in Bubble Sort is always 1, but the Comb Sort allows for the gap to be larger than 1 and then shrink by (k) for each iteration. (k) highly affects the efficiency of the algorithm, and is ideal at 1.3.
Properties
- Best time Complexity : O(n)
- Worst time Complexity: O(n^2)
Sources to read:
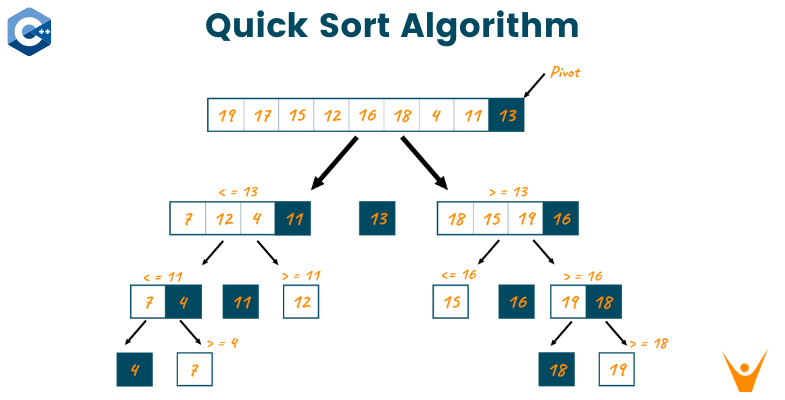
QuickSort is a Divide and Conquer algorithm. It picks an element as a pivot and partitions the given array around the picked pivot. There are 4 common ways of selecting a pivot:
- Pick the first element
- Pick the last element
- Pick a random element
- Pick the median element
The key process in quickSort is a partition(). The target of partitions is, given an array and an element x of an array as the pivot, put x at its correct position in a sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear time.
Properties
- Average time complexity : O(n log n)
- Worst time complexity: O(n^2)
Sources to read:
The selection sort algorithm sorts an array by repeatedly finding the minimum element (considering ascending order) from the unsorted part and putting it at the beginning.
The algorithm maintains two subarrays in a given array.
- The subarray which already sorted.
- The remaining subarray was unsorted.
In every iteration of the selection sort, the minimum element (considering ascending order) from the unsorted subarray is picked and moved to the sorted subarray.
Properties
- Worst/Average time complexity : Ο(n2), where n is the number of items
Sources to read:
Heap sort is a comparison-based sorting algorithm that uses a binary heap data structure. The main idea behind heap sort is to turn the array into a max-heap structure, which ensures that the largest element of the heap is located at the root. This largest element is then swapped with the last element and removed from the heap. This process is repeated until the heap is empty, resulting in a sorted array.
- Safety: One of Rust's main features is memory safety. In the heap sort implementation, Rust ensures safety by using borrowing and the slice notation to manipulate parts of the array.
- In-place Swapping: Rust provides an efficient way to swap two elements in an array with arr.swap(i, j), which makes the algorithm elegant and concise.
- Performance: Rust, being a systems programming language, ensures that the heap sort implementation is efficient and can be optimized further by the Rust compiler.
Properties
- In-place sorting: It sorts the data in place, requiring only a constant amount of additional memory.
- Time complexity: Heap sort has a worst-case time complexity of O(n log n).
Sources to read:
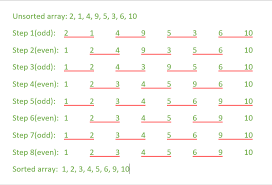
Odd-Even Sort, also known as Brick Sort, is a relatively simple sorting algorithm, inspired by the idea behind Bubble Sort. The main idea is to repeatedly make two passes on an array: one for every odd-indexed element pair and the other for every even-indexed element pair.
Algorithm
- Odd Step: Compare all odd-indexed elements of the array with their next neighbor (i.e., at index i and i+1) and swap them if the element at index i is greater than the one at i+1.
- Even Step: Compare all even-indexed elements of the array with their next neighbor (i.e., at index i and i+1) and swap them if the element at index i is greater than the one at i+1.
- Repeat the two steps until the array is sorted.
Properties
- Worst case : O(n^2)
- Best case : O(n)
- Average case : O(n^2)
Sources to read:
The main operation in Pancake Sort is a "flip" operation. Given an integer k, the flip operation reverses the order of the first k elements in the array.
The idea behind Pancake Sort:
- Find the index of the maximum element in the array.
- Use the flip operation to move this maximum element to the beginning of the array.
- Use another flip operation to move this maximum element to its correct position at the end of the array.
- Exclude the last element and repeat the above steps for the rest of the array.
The goal is to move the largest unsorted element to its correct position in each iteration.
Properties
- Worst case : O(n^2)
- Average case : O(n^2)
Sources to read:
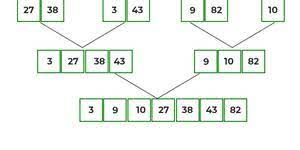
Merge sort is a divide-and-conquer sorting algorithm. It works as follows:
-
Divide the unsorted list into n sublists, each containing one element.
-
Repeatedly merge sublists to produce new sorted sublists until there is only one sublist remaining.
-
The merge_sort function first checks if the array has a length of 1 or 0. If so, it's already sorted, so it returns the array as-is.
-
The array is split into two halves, which are recursively sorted.
-
The sorted halves are merged together using the merge function.
-
The merge function takes two sorted arrays (or slices) and returns a new array that contains all the elements from both arrays in sorted order. It does this by iterating through both arrays simultaneously, always choosing the smallest of the two current elements to append to the result.
Properties
- Worst case : O(nlogn)
- Average case : O(nlogn)
- Best case : O(nlogn)
Sources to read:
Insertion sort is a simple and intuitive sorting algorithm that builds the final sorted array one element at a time. It's best suited for small arrays or arrays that are already nearly sorted.
The basic idea of insertion sort is similar to the way many people sort playing cards in their hands. We start from the beginning of the array and continuously insert elements in their correct position in the sorted portion of the array.
Here's a step-by-step explanation followed by a Rust implementation:
- Start from the second element (index 1) assuming the element at index 0 is sorted.
- Compare the current element with the previous elements. If the current element is smaller than the previous element, we keep comparing with the elements before until we reach an element smaller or reach the start of the array.
- Insert the current element in its correct position so that the elements before are all smaller than the current element.
- Repeat the process for each of the elements in the array.
Properties
- Worst case : O(n^2)
- Average case : O(n^2)
- Best case : O(n)
Space Complexity
- O(1) - Because it's an in-place sorting algorithm (i.e., it doesn't require any additional storage).
Sources to read:
Strand Sort is a sorting algorithm that works by repeatedly pulling sorted sublists out of the list to be sorted and merging them with the already sorted part. It is particularly effective for sorting lists where there are large numbers of ordered elements. The algorithm is intuitive and simple, iterating through the list, picking up elements in order, and merging these 'strands' into a final sorted list.
- Simplicity: The algorithm is straightforward and easy to implement, making it a good choice for introductory sorting algorithm education.
- Adaptive: Strand sort performs well on lists that are already partially sorted, as it can quickly identify and extract these ordered sublists.
- In-place Sorting: The nature of the algorithm allows it to be implemented in an in-place fashion, although this is not always the case.
Properties
- Not-in-place Sorting: Typically, strand sort requires additional space for the strands, though in-place variants exist.
- Time Complexity: The average and worst-case time complexity of strand sort can vary greatly depending on the input but typically is O(n²).
- Stability: The algorithm is stable, maintaining the relative order of equal elements.
Sources to read:
Pigeonhole Sort is a sorting algorithm that is efficient for sorting data with a known, limited range of key values. It works by creating an array of 'holes' (each representing a position in the range of the data) and then sorting the data by 'placing' each item into its corresponding hole. The algorithm then collects the items from each hole in order, resulting in a sorted array.
The Rust implementation of Pigeonhole Sort involves the following steps:
-
Initialization: First, it checks if the input array is empty. If so, it returns immediately as there's nothing to sort.
-
Finding the Range: The implementation identifies the minimum and maximum values in the array. The range is the difference between these values plus one.
-
Creating Holes: A vector of vectors (
Vec<Vec<i32>>) is created to represent the holes. The size of this outer vector is equal to the range of the input data. -
Filling the Holes: The algorithm iterates over each element in the array, placing it into the corresponding hole based on its value.
-
Reconstructing the Array: Finally, it iterates over the holes in order, placing each element back into the original array, now sorted.
Tree Sort is a sorting algorithm that builds a binary search tree from the elements of the array to be sorted and then performs an in-order traversal to generate a sorted array. The essence of tree sort lies in leveraging the properties of a binary search tree, where elements are inserted in such a way that for any given node, all elements in the left subtree are less than the node and all elements in the right subtree are greater.
- Safety: Rust’s adherence to memory safety is a significant asset in the implementation of tree sort. The algorithm makes use of Rust's ownership and borrowing rules to manage the tree structure without the risk of memory leaks or dangling pointers.
- Tree Construction: Rust’s powerful data handling capabilities facilitate the efficient construction and manipulation of the binary search tree, a crucial aspect of tree sort.
- Performance: While not the most efficient in all cases, tree sort in Rust can be quite performant especially for datasets that are not large, thanks to Rust's optimization capabilities.
Properties
- Not-in-place sorting: Tree sort requires additional memory for the binary search tree, hence it's not an in-place sorting algorithm.
- Time complexity: The average case time complexity of tree sort is O(n log n), but it can degrade to O(n²) in the worst case when the tree becomes unbalanced.
Sources to read: