Напомним, что отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Вектор на плоскости можно задать двумя числами — его координатами по горизонтали и вертикали.
Помимо очевидных сложения, вычитания и умножения на константу (скаляр — одно число), у векторов можно ввести и свои особенные операции, которые нам упростят жизнь.
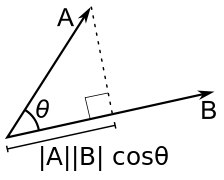
Скалярное произведение (англ. dot product) — произведение длин векторов на косинус угла между ними. Для него справедлива следующая формула:
Она доказывается муторно и чисто технически, так что мы это делать не будем.
Геометрически, она равна проекции вектора
У него есть полезные свойства:
- Скалярное произведение симметрично (
). - Перпендикулярные вектора должны иметь нулевое скалярное произведение.
- Если угол острый, то скалярное произведение положительное.
- Если угол тупой, то скалярное произведение отрицательное.
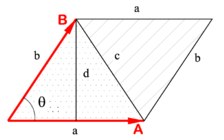
Векторное произведение (англ. cross product) — произведение длин векторов на синус угла между ними, причём знак этого синуса зависит от порядка операндов. Оно тоже удобно выражается в координатах:
Геометрически, это ориентированный объем параллелограмма, натянутого на вектора
Его свойства:
- Векторное произведение антисимметрично:
. - Коллинеарные вектора должны иметь нулевое векторное произведение.
- Если
«слева» от , то векторное произведение положительное. - Если
«справа» от , то векторное произведение отрицательное.
Вообще говоря, векторное произведение определяется не так. Оно определено как вектор такой же длины, но перпендикулярный обоим исходным векторам. Это имеет применение в трёхмерной геометрии и физике, но нам об этом думать не надо.
Благодаря этим свойствам, почти все проверки в геометрии можно описать через них, а не уравнениями.
Принадлежность точки треугольнику. Пусть у нас есть треугольник
Площадь треугольника. Можно пользоваться готовыми формулами, а можно и свойством векторного произведения.
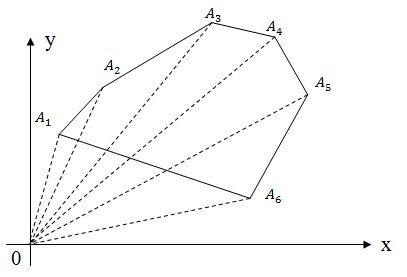
Площадь произвольного многоугольника. Если многоугольник задан последовательностью вершин в каком-то порядке, то можно считать так: для каждого ребра добавим его ориентированную площадь от начала координат. Какие-то слагаемые будут положительными (которые на последнем слое, а какие-то — отрицательными).
Забудьте о формуле Герона и всегда считайте площади через векторное произведение.
Кстати, из формулы для площади треугольника следует, что площадь любой фигуры будет либо целым числом, либо рациональным с двойкой в знаменателе. Часто в в задачах входные данные целочисленные, и, чтобы оставаться в целых числах, когда мы считаем какую-нибудь площадь, иногда имеет смысл умножить все входные числа на
Проверка на выпуклость. Можно пройтись по сторонам многоугольника и проверять векторным произведением, что мы поворачиваем всегда в одну сторону, то есть для всех последовательных точек
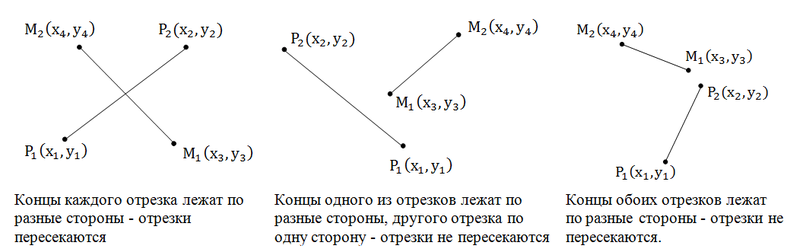
Пересекаются ли отрезки.
Прямую можно задать уравнением вида
У прямой есть вектор нормали с координатами
Чтобы найти расстояние от точки
Точка пересечения. По сути, найти точку пересечения двух прямых — это то же самое, что и найти точку, которая удовлетворяет обоим условиям их уравнений:
Аналогично,
Заметим, что знаменатель может оказаться нулем. Это означает, что векторное произведение векторов нормали нулевое, а значит прямые параллельны (в частности, это могут быть совпадающие прямые). Этот случай нужно обрабатывать отдельно.
Небольшой ликбез по объектно-ориентированному программированию в C++. Создадим класс, который будет отвечать за все операции с точками. В C++ есть два способа это сделать: через struct и через class. Их основное отличие в том, что по умолчанию в class все поля приватные — к ним нет прямого доступа снаружи. Это нужно для дополнительной защиты, чтобы в крупных промышленных проектах никто случайно ничего не поломал, но на олимпиадах это не очень актуально.
Точка r. Вы можете обозвать их как point, pt, vec — как угодно.
struct r {
double x, y;
r() {}
r(int _x, int _y) { x = _x, y = _y; }
};Функция r внутри класса вызывается при инциализации объекта. Её называют конструктором, и её можно указывать разную для разных параметров. Здесь r()вернёт точку с неопределенными (какие оказались в памяти в тот момент) координатами, а r(x, y) вернет точку с координатами
Давайте напишем функцию, которая принимает вектора и что-то с ними делает. Например, считает длину:
double len(r a) { return sqrt(a.x*a.x + a.y*a.y); }В C++ можно перегружать почти все стандартные операторы, например, +, -, << и т. д.
Переопределим для будущих нужд + и -:
r operator+(r a, r b) { return r(a.x+b.x, a.y+b.y); }
r operator-(r a, r b) { return r(a.x-b.x, a.y-b.y); }Скалярное произведение:
int operator*(r a, r b) { return a.x*b.x + a.y*b.y; }Векторное произведение:
int operator^(r a, r b) { return a.x*b.y - b.x*a.y; }Как вы думаете, как на самом деле работает cin >> x? Это тоже перегрузка оператора — >>. Делается это так:
istream& operator>>(istream &in, r &p) {
in >> p.x >> p.y;
return in;
}
ostream& operator<<(ostream &out, r &p) {
out << p.x << " " << p.y << endl;
return out;
}Мы могли не создавать никаких структур и работать с уравнениями, описывающими геометрические объекты. Такой подход будет популярен на олимпиадах по математике, а не по программированию. Когда математик говорит «пересечем две прямые», он представляет громоздкое уравнение, с которым он потом будет работать.
Программист же хочет абстрагироваться и просто написать intersect(a, b), в корректности которого он точно уверен. Программист хочет разбить задачу на много маленьких кусочков и делать по отдельности, а не возиться с формулами.
Приведем несколько примеров конструктивного подхода.
Прямую можно задать не через уравнение, а через два вектора
Чтобы это сделать, достаточно выбрать две любые точки на прямой:
// даны A, B, C (A^2 + B^2 != 0)
r a, b;
if (eq(A, 0)) // значит, это горизонтальная прямая
a = r(0, -C/B), b = r(1, -C/B);
else
a = r(-C/A, 0), b = (1, -(C+B)/A, 1)Пусть нам надо отразить точку
Геометрический смысл: длина на единичный вектор направления.
Мы не хотим раскрывать эти формулы покоординатно и предъявлять готовый ответ. Мы знаем, что он получится громоздким. Нам не жалко посчитать всё по частям — здесь нет смысла заниматься оптимизациями. Также мы хотим делать всё по частям, потому что так становится более наглядной логика алгоритма, и, как следствие, его проще дебажить.
// прямая r = at + b, точка c
r pr (r a, r b, r c) {
c -= b; // пусть c и a выходят из одной точки
return b + (a*b / len(a) / len(a)) * a;
}
r reflect (r a, r b, r c) {
return c + 2*(pr(a, b, c)-c);
}Первое правило действительных чисел — не использовать действительные числа
Все переменные типа double хранятся в компьютере неточно (ну а как вы представите ⅓ в двоичной системе счисления?). Поэтому при работе с даблами нужно всегда учитывать эту погрешность. Например, чтобы сравнить два дабла, надо проверить, что они отличаются по модулю меньше, чем на очень маленькое число eps:
const double eps = 1e-8;
bool eq (double a, double b) { return abs(a-b) < eps }Чтобы так не делать, старайтесь по возможности использовать только инты и абсолютную точность. Иногда есть трюки, позволяющие так делать: например, если в задаче все входные точки целочисленные и нас просят посчитать какую-то площадь, то можно все координаты домножить на два, и тогда ответ тоже будет целым (см. векторное произведение), который только при выводе нужно будет поделить на четыре.
Действительные числа так хранятся, что
acos, asin и прочие обратные тригонометрические функций требуют, чтобы им на вход подавалось число от -1 до 1. Для безопасности, отмасштабируйте числа, перед тем как брать от них эти функции.