lca.md

Корневые деревья

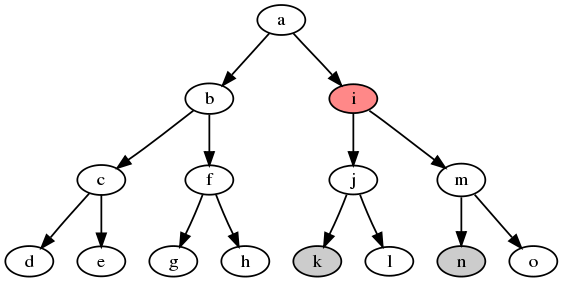
Дерево называется корневым, если оно ориентированно, и из какой-то вершины (называемой корнем) можно попасть во все остальные.

Примеры корневых деревьев:

• наследование классов в языках программирования (если множественное наследование запрещено),
• дерево факторизации числа на простые (в общем случае не уникальное),
• иерархия в какой-нибудь организации,
• дерево парсинга математичеких выражений.

Задачи на корневые деревья весьма бесполезны в реальной жизни, но зато очень интересны с алгоритмической точки зрения, и поэтому часто встречаются на олимпиадах по программированию.

Свойства dfs

Посчитаем для каждой вершины времена входа ($tin$) и выхода ($tout$) из неё во время эйлерова прохода:

vector<int> g[maxn];
int p[maxn], tin[maxn], tout[maxn];
int t = 0;

void dfs (int v) {
    tin[v] = t++;
    for (int u : g[v])
        dfs(u);
    tout[v] = t; // иногда счётчик тут тоже увеличивают
}

У этих массивов много полезных свойств:

• Вершина $u$ является предком $v$ $\iff tin_v \in [tin_u, tout_u)$. Эту проверку можно делать за константу.
• Два полуинтервала — $[tin_v, tout_v)$ и $[tin_u, tout_u)$ — либо не пересекаются, либо один вложен в другой.
• В массиве $tin$ есть все числа из промежутка от 0 до $n-1$, причём у каждой вершины свой номер.
• Размер поддерева вершины $v$ (включая саму вершину) равен $tout_v - tin_v$.
• Если ввести нумерацию вершин, соответствующую $tin$-ам, то индексы любого поддерева всегда будут каким-то промежутком в этой нумерации.

Запросы на поддеревьях

Последнее свойство на самом деле очень важное. Его можно использовать для обработки разных запросов на поддеревьях, сводя их к запросам на подотрезках, которые уже можно решать стандартными методами — например, через дерево отрезков.

Пример задачи:

Есть корневое дерево. Рядом с каждой вершиной записано число. Поступают два типа запросов: прибавить ко всем вершинам на каком-то поддереве число $x_i$ и найти значение числа у вершины $v_i$.

Выпишем все числа у вершин в один массив, в позиции, соответствующие их $tin$-ам. Что такое «прибавить на поддереве» относительно этого массива? Это то же, самое, что прибавить какую-то константу на каком-то подотрезке, а это можно делать любой достаточно продвинутой структурой.

Запросы на уровнях

Дано корневое дерево. Требуется отвечать на запросы нахождения $d_i$-того предка вершины $v_i$, то есть вершины-предка, находящейся на расстоянии $d_i$ от $v_i$.

Создадим $h$ векторов, где $h$ — высота дерева. Для каждой вершины, во время прохода в dfs, добавим её $tin$ в вектор, соответствующей её глубине. Получаем $h$ отсортированных векторов.

Теперь заметим, что внутри одного вектора все отрезки поддеревьев вершин — $[tin_v, tout_v)$ — тоже не пересекаются, а значит ещё и отсортированы. Тогда ответа на запрос мы можем просто взять $tin$ вершины-запроса, посмотреть на вектор нужного уровня и за $O(\log n)$ сделать бинпоиск по нужному отрезку.

Также существует другой способ, требующий $O(1)$ времени на запрос, но $O(n \log n)$ памяти на предпосчёт — лестничная декомпозиция.

Наименьший общий предок

Для большого класса задач требуется решить следующую вспомогательную:

Дано корневое дерево. Требуется отвечать на запросы нахождения наименьшего общего предка вершин $u_i$ и $v_i$, то есть вершины $w$, которая лежит на пути от корня до $u_i$, на пути от корня до $v_i$, и при этом самую глубокую (нижнюю) из всех таких.

По-английский эта задача называется Least Common Ancestor. Есть много разных способов её решать, и мы рассмотрим только основные.

Для лучшего понимания — медленно (за линейное время) наименьшего общего предка можно искать так:

bool a (int u, int v) {
    return tin[u] <= tin[v] && tin[v] < tout[u];
}

int lca (int u, int v) {
    while (!ancestor(u, v))
        u = p[u];
    return u;
}

Двоичные подъемы

Предпосчитаем для каждой вершины её 1-го предка, 2-го предка, 4-го и так далее. Сохраним их в двумерном массиве up размера $n \times \lceil \log n \rceil$: в up[v][d] будет храниться предок вершины $v$ на расстоянии $2^d$, а если такой вершины не существует, то корень.

Такой препроцессинг можно выполнить за $O(n \log n)$, используя тот факт, что предок на расстоянии $2^{d+1}$ — это предок на расстоянии $2^d$ предка на расстоянии $2^d$:

int up[maxn][logn];

void dfs (int v) {
    for (int l = 1; l < logn; l++)
        up[v][l] = up[up[v][l-1]][l-1];
    tin[v] = t++;
    for (int u : g[v]) {
        up[u][0] = v;
        dfs(u);
    }
    tout[v] = t;
}

Пусть теперь поступил запрос нахождения LCA — пара вершин $(u, v)$:

• Проверим, не является ли одна вершина предком другой — в таком случае она и является результатом.
• Иначе, пользуясь массивом up, будем подниматься по предкам одной из них, пока не найдём самую высокую вершину, которая ещё не является предком другой. Следующая за ней будет искомым LCA.

Подробнее про второй пункт. Присвоим $i = \lceil \log n \rceil$ и будем уменьшать эту переменную на единицу, пока up[v][i] не перестанет быть предком $u$. Когда это произойдёт, подвинем указатель на $2^i$-го предка $v$ и продолжим дальше:

int lca (int v, int u) {
    if (a(v, u)) return v;
    if (a(u, v)) return u;
    for (int l = logn-1; l >= 0; l--)
        if (!ancestor(up[v][l], u))
            v = up[v][l];
    return up[v][0];
}

Указатель up[v][i] изначально явдяеься корнем дерева, а затем будет каждую итерацию спускаться на $2^i$. Когда он станет потомком lca, нам достаточно подняться всего лишь один раз, потому что два раза прыгнуть на расстояние $2^i$ это то же самое, что один раз прыгнуть на $2^{i+1}$, а мы могли это сделать на предыдущем шаге.

Асимптотика. Препроцессинг занимает $O(n \log n)$, потому что таков размер массива up, и каждый его элемент вычисляется за константу. Ответ на произвольный запрос будет работать за $O(\log n)$, потому что фактически мы делаем один бинпоиск.

Запросы на путях

Пусть нас вместо LCA спрашивают, например, о минимуме на произвольном пути (на всех рёбрах записаны какие-то числа).

Мы можем сделать такой же предподсчет, как в методе двоичных подъемов, но хранить вместе с номером $2^d$-ого предка минимум на соответствующем пути.

Заметим, что минимум на пути от $u$ до $v$ — это минимум от минимума на пути от $u$ до $lca(u, v)$ и от минимума на пути от $v$ до $lca(u, v)$. В свою очередь, оба этих минимума — это минимум на всех двоичных подъемах до LCA.

int get_min (int v, int u) {
    int res = inf;
    for (int l = logn-1; l >= 0; l--)
        if (!ancestor(up[v][l], u))
            v = up[v][l], res = min(res, mn[v][l]);
    for (int l = logn-1; l >= 0; l--)
        if (!ancestor(up[u][l], v))
            u = up[u][l], res = min(res, mn[u][l]);
    return min({res, mn[v][0], mn[u][0]})
}

Аналогичным образом можно считать сумму, gcd, полиномиальный хэш и много других странных функций на пути, но только в статическом случае (когда у нас нет обновлений). Для динамического случая существует весьма сложный метод, называемый heavy-light декомпозицией.

Сведение LCA к RMQ

Подойдём к задаче нахождения наименьшего общего предка с другой стороны.

Пройдёмся по дереву dfs-ом и выпишем два массива: глубины вершин и номера вершин. Записывать мы их будем как когда при входе в вершину, так и при выходе.

Пусть теперь поступил запрос: найти LCA вершин $v$ и $u$. Для определенности предположим, что $tin_v < tin_u$, то есть $v$ в обходе встретилась раньше. Посмотрим на часть выписанного пути между моментом, когда мы вышли из $v$ и моментом, когда мы в первый раз вошли в $u$. Где-то на этом отрезке мы должны были прийти в наименьший общий предок, так как любой простой путь между двумя вершинами в дереве единственный. При этом мы на этом пути не поднимались куда-то выше LCA, а значит LCA — это самая высокая вершина на этом пути.

Получается, что чтобы найти LCA, можно найти позицию минимума на отрезке $[tout_v, tin_u]$ в массиве глубин (первый выписанный массив) и посмотреть, какой вершине она соответствует в эйлеровом обходе (второй выписанный массив). Таким образом, задачу LCA можно свести к задаче RMQ (нахождению минимума на отрезке), что можно сделать тем же деревом отрезков.

Разреженная таблица

На практике асимптотику мы особо не улучшили — пока что всё равно требуется $O(\log n)$ времени на запрос в дерево отрезков, хоть преподсчёт и будет уже линейным.

Асимптотику времени запроса можно улучшить, используя тот факт, что мы на самом деле решаем задачу static RMQ, то есть у нас нет изменений этого массива. Для этого есть более подходящая структура — разреженная таблица. Она позволяет отвечать на запрос минимума за $O(1)$, но использует $O(n \log n)$ операций на препроцессинг (с малой константой). Подробнее про неё можно почитать в отдельной статье.

Алгоритм Фарах-Колтона и Бендера

Примечание: алгоритм нахождения RMQ, описываемый в этой секции, абсолютно бесполезен на практике, однако очень интересен с теоретической точки зрения.

Оказывается, что и LCA, и static RMQ можно считать за $O(1)$ времени на запрос и $O(n)$ времени на предпосчёт.

На самом деле, мы решаем не совсем полноценную задачу RMQ. Мы работаем не со всеми массивами целых чисел от 1 до $n$, а только с некоторыми — с теми, в которых любые два элемента отличаются ровно на единицу, потому что каждый переход это либо спуск, либо подъём в dfs. Это ограничение позволяет находить минимум на подотрезках подобных массивов быстрее.

Сделаем следующее: раз каждые два элемента отличаются на единицу, то сопоставим исходному массиву глубин булевый массив размера $(n-1)$: на $i$-той позиции будет стоять единица, если следующее значение больше, и ноль в противном случае. Этот массив нужно будет хранить в бинарном виде, чтобы можно было за константу получать булеву маску небольших подотрезков.

Первая часть предподсчёта. Возьмем константу $k = \lfloor \frac{\log n}{2} \rfloor$, и разделим исходный массив на блоки по $k$ элементов. На каждом блоке посчитаем минимум, а над этими минимумами построим sparse table.

Всего блоков таких блоков $O(\frac{2 n}{\log n})$, и поэтому построение работает за линейное время:

$$ O(\frac{2 n}{\log n} \log \frac{2 n}{\log n}) = O(\frac{2 n}{\log n} (\log 2n - \log \log n)) = O(n) $$

Вторая часть предподсчёта. Посчитаем для каждой возможной маски подъёмов / спусков размера $k$ максимальный спуск на ней — то есть пройдёмся по ней, поддерживая разницу встретившихся нулей и единиц, и запомним минимальное значение этого баланса. Это можно сделать за длину маски, помоноженное на их количество:

$$ O(k \cdot 2^k) = O(\frac{\log n}{2} 2^{\frac{\log n}{2}}) = O(\sqrt n \log n) $$

Возможных масок получается немного — ради этого мы и делили логарифм на два при определении $k$

Запрос. Нам нужно с помощью посчитанных структур найти RMQ на каком-то отрезке $[l, r]$. Он включает в себя какие-то последовательные блоки и сколько-то оставшихся ячеек слева и справа, не вошедших ни в какой целый блок.

• Для блочной части мы можем просто сделать запрос в sparse table — он будет работать за константу.

• Для обеих не-блочных частей посчитаем ещё по кандидату на ответ. Для этого нужно прибавить к граничному элементу предподсчитанное значение минимума на маске оставшихся неблочных элементов — её можно за константу получить битовыми операциями над булевым массивом.

Просто посчитать все суффиксные и префиксные минимумы для всех блоков, чтобы обрабатывать второй случай, к сожалению, нельзя — есть один частный случай, когда запрос маленький и не накрывает никакой блок целиком. В данном случае нужно просто взять граничный элемент и прибавить к нему минимум от нужной маски из массива подъёмов.

Наоборот. Этот алгоритм очень важен с теоретической точки зрения, потому что позволяет решать, не только LCA, но и в общем случае static RMQ за линейное время.

Построим декартово дерево, в котором в качестве ключей $x_i$ возьмём индексы элементов, а в качестве приоритетов $y_i$ возьмём сами значения. Декартово дерево могло получиться несбалансированным (так как нет рандомизации приоритетов), но это нам и не нужно. Дальше просто применим описанный выше алгоритм к этому дереву, и теперь для нахождения минимума в исходном массиве можно просто запросить общего предка $l$-той и $r$-той вершины в дереве — его приоритет в декартовом дереве и будет искомым минимумом.

Чуть более подробно и с реализацией (автор это никогда не кодил и вам не советует) можно почитать у Емакса. Впрочем, на практике этот алгоритм использовать нецелесообразно из-за большой константы: слишком много чего нужно считать, чтобы избавиться от логарифма в асимптотике.