BAYEX: Bayesian Optimization powered by JAX

Features | Installation | Usage | Contributing

Bayex is a high performance Bayesian global optimization library using Gaussian processes. In contrast to existing Bayesian optimization libraries, Bayex is completly written in JAX.

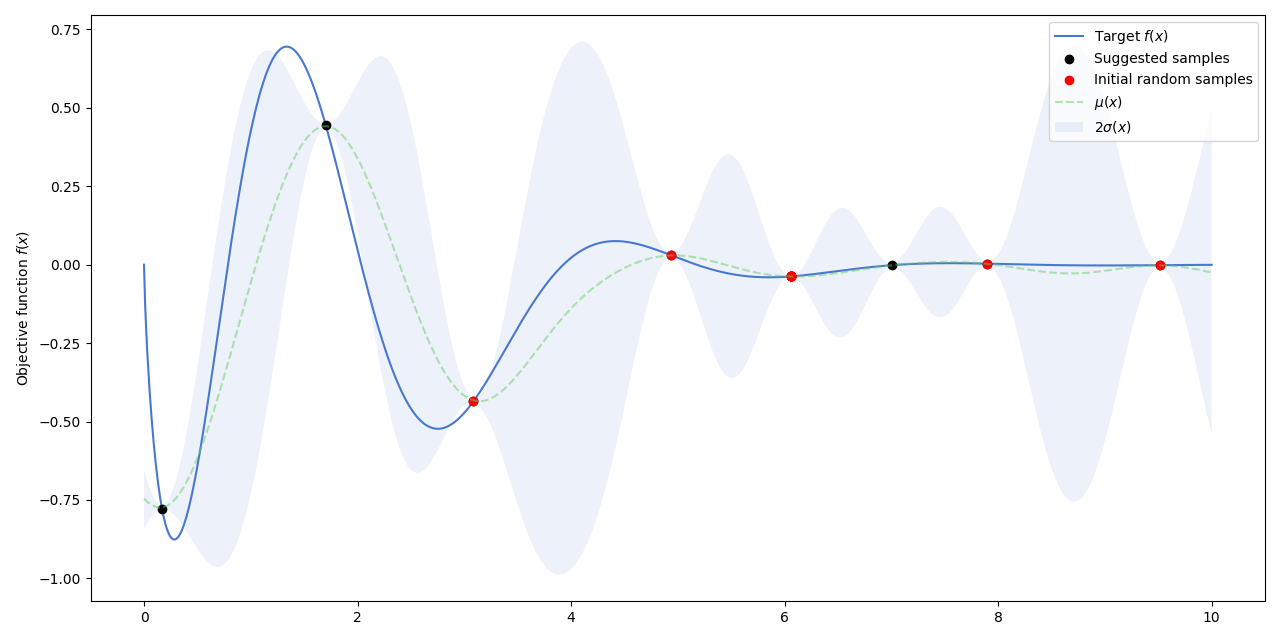
Bayesian Optimization (BO) methods are useful for optimizing functions that are expensive to evaluate, lack an analytical expression and whose evaluations can be contaminated by noise. These methods rely typically on a Gaussian process (GP), upon which an acquisition function guides the optimization process and measures the expected utility of performing an evaluation of the objective at a new suggested point.

Features

• High Performance: by making use of vectorization and JIT compilation provided by JAX.
• Hardware Accelerated: Bayex can be run on CPU, but also on GPU and TPU wihtout issues.
• Discrete variables: Support for discrete variables.
• Multiple Acquisition Functions: Expected Improvement, Probability of Improvement, Upper/Lower Confidence Bound, etc.
• Multiple Kernel choices: Squared Exponential, Mattern (0.5, 1.0, 1.5), Periodic, etc.

Installation

Bayex can be installed using PyPI via pip:

pip install bayex

or from GitHub directly

pip install git+git://github.com/alonfnt/bayex.git

For more advance instructions please refer to the installation guide.

Usage

Using Bayex is very straightforward:

import bayex

def f(x, y):
    return -y ** 2 - (x - y) ** 2 + 3 * x / y - 2

constrains = {'x': (-10, 10), 'y': (0, 10)}
optim_params = bayex.optim(f, constrains=constrains, seed=42, n=10)

showing the results can be done with

>> bayex.show_results(optim_params)
   #sample      target          x            y
      1        -9.84385      2.87875      3.22516
      2        -307.513     -6.13013      8.86493
      3        -19.2197      6.8417       1.9193
      4        -43.6495     -3.09738      2.52383
      5        -58.9488      2.63803      6.54768
      6        -64.8658      4.5109       7.47569
      7        -78.5649      6.91026      8.70257
      8        -9.49354      5.56705      1.43459
      9        -9.59955      5.60318      1.39322
     10        -15.4077      6.37659      1.5895
     11        -11.7703      5.83045      1.80338
     12        -11.4169      2.53303      3.32719
     13        -8.49429      2.67945      3.0094
     14        -9.17395      2.74325      3.11174
     15        -7.35265      2.86541      2.88627

we can also obtain the maximum value found using

>> optim_params.target
-7.352654457092285

as well as the input parameters that yield it

>> optim_params.params
{'x': 2.865405, 'y': 2.8862667}