README.md

剑指 Offer II 107. 矩阵中的距离

题目描述

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

 

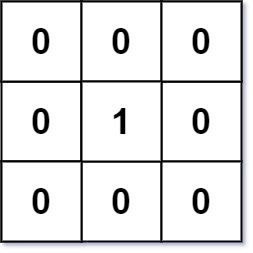
示例 1：

输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

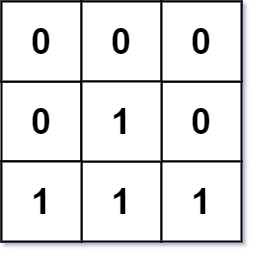
示例 2：

输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

 

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0 

 

注意：本题与主站 542 题相同：https://leetcode.cn/problems/01-matrix/

解法

方法一：多源 BFS

初始化结果矩阵 ans，所有 0 的距离为 0，所以 1 的距离为 -1。初始化队列 q 存储 BFS 需要检查的位置，并将所有 0 的位置入队。

循环弹出队列 q 的元素 p(i, j)，检查邻居四个点。对于邻居 (x, y)，如果 ans[x][y] = -1，则更新 ans[x][y] = ans[i][j] + 1。同时将 (x, y) 入队。

Python3

class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        m, n = len(mat), len(mat[0])
        ans = [[-1] * n for _ in range(m)]
        q = deque()
        for i, row in enumerate(mat):
            for j, v in enumerate(row):
                if v == 0:
                    ans[i][j] = 0
                    q.append((i, j))
        dirs = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        while q:
            i, j = q.popleft()
            for a, b in dirs:
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and ans[x][y] == -1:
                    ans[x][y] = ans[i][j] + 1
                    q.append((x, y))
        return ans

Java

class Solution {

    public int[][] updateMatrix(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[][] ans = new int[m][n];
        for (int i = 0; i < m; ++i) {
            Arrays.fill(ans[i], -1);
        }
        Deque<int[]> q = new LinkedList<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 0) {
                    ans[i][j] = 0;
                    q.offer(new int[] {i, j});
                }
            }
        }
        int[] dirs = new int[] {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            int[] t = q.poll();
            for (int i = 0; i < 4; ++i) {
                int x = t[0] + dirs[i];
                int y = t[1] + dirs[i + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
                    ans[x][y] = ans[t[0]][t[1]] + 1;
                    q.offer(new int[] {x, y});
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> ans(m, vector<int>(n, -1));
        queue<pair<int, int>> q;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 0) {
                    ans[i][j] = 0;
                    q.emplace(i, j);
                }
            }
        }
        vector<int> dirs = {-1, 0, 1, 0, -1};
        while (!q.empty()) {
            auto p = q.front();
            q.pop();
            for (int i = 0; i < 4; ++i) {
                int x = p.first + dirs[i];
                int y = p.second + dirs[i + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
                    ans[x][y] = ans[p.first][p.second] + 1;
                    q.emplace(x, y);
                }
            }
        }
        return ans;
    }
};

Go

func updateMatrix(mat [][]int) [][]int {
	m, n := len(mat), len(mat[0])
	ans := make([][]int, m)
	for i := range ans {
		ans[i] = make([]int, n)
		for j := range ans[i] {
			ans[i][j] = -1
		}
	}
	type pair struct{ x, y int }
	var q []pair
	for i, row := range mat {
		for j, v := range row {
			if v == 0 {
				ans[i][j] = 0
				q = append(q, pair{i, j})
			}
		}
	}
	dirs := []int{-1, 0, 1, 0, -1}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		for i := 0; i < 4; i++ {
			x, y := p.x+dirs[i], p.y+dirs[i+1]
			if x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1 {
				ans[x][y] = ans[p.x][p.y] + 1
				q = append(q, pair{x, y})
			}
		}
	}
	return ans
}

...