https://leetcode.com/problems/subarray-sum-equals-k/description/
Given an array of integers and an integer k, you need to find the total number of continuous subarrays whose sum equals to k.
Example 1:
Input:nums = [1,1,1], k = 2
Output: 2
Note:
The length of the array is in range [1, 20,000].
The range of numbers in the array is [-1000, 1000] and the range of the integer k is [-1e7, 1e7].
The simplest method is Brute-force. Consider every possible subarray, find the sum of the elements of each of those subarrays and check for the equality of the sum with k. Whenever the sum equals k, we increment the count. Time Complexity is O(n^2). Implementation is as followed.
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
cnt, n = 0, len(nums)
for i in range(n):
for j in range(i, n):
if (sum(nums[i:j + 1]) == k): cnt += 1
return cntIf we implement the sum() method on our own, we get the time of complexity O(n^3).
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
cnt, n = 0, len(nums)
for i in range(n):
for j in range(i, n):
sum = 0
for x in range(i, j + 1):
sum += nums[x]
if (sum == k): cnt += 1
return cntAt first glance I think "maybe it can be solved by using the sliding window technique". However, I give that thought up when I find out that the given array may contain negative numbers, which makes it more complicated to expand or narrow the range of the sliding window. Then I think about using a prefix sum array, with which we can obtain the sum of the elements between every two indices by subtracting the prefix sum corresponding to the two indices. It sounds feasible, so I implement it as followed.
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
cnt, n = 0, len(nums)
pre = [0] * (n + 1)
for i in range(1, n + 1):
pre[i] = pre[i - 1] + nums[i - 1]
for i in range(1, n + 1):
for j in range(i, n + 1):
if (pre[j] - pre[i - 1] == k): cnt += 1
return cntActually, there is a more clever way to do this. Instead of using a prefix sum array, we use a hashmap to reduce the time complexity to O(n).
Algorithm:
-
We make use of a hashmap to store the cumulative sum
accand the number of times the same sum occurs. We useaccas thekeyof the hashmap and the number of times the sameaccoccurs as thevalue. -
We traverse over the given array and keep on finding the cumulative sum
acc. Every time we encounter a newaccwe add a new entry to the hashmap. If the sameaccoccurs, we increment the count corresponding to thataccin the hashmap. Ifaccequalsk, obviouslycountshould be incremented. Ifacc - kgot, we should incrementaccountbyhashmap[acc - k]. -
The idea behind this is that if the cumulative sum upto two indices is the same, the sum of the elements between those two indices is zero. So if the cumulative sum upto two indices is at a different of
k, the sum of the elements between those indices isk. Ashashmap[acc - k]keeps track of the number of times a subarray with sumacc - khas occured upto the current index, by doing a simple substractionacc - (acc - k)we can see thathashmap[acc - k]actually also determines the number of times a subarray with sumkhas occured upto the current index. So we increment thecountbyhashmap[acc - k].
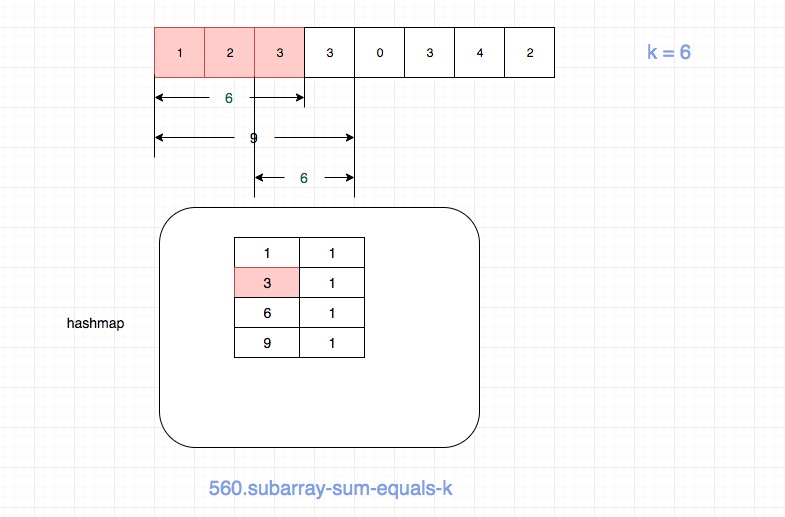
Here is a graph demonstrating this algorithm in the case of nums = [1,2,3,3,0,3,4,2], k = 6.
When we are at nums[3], the hashmap is as the picture shows, and count is 2 by this time. [1, 2, 3] accounts for one of the count, and [3, 3] accounts for another.
The subarray [3, 3] is obtained from hashmap[acc - k], which is hashmap[9 - 6].
- Prefix sum array
- Make use of a hashmap to track cumulative sum and avoid repetitive calculation.
JavaScript Code
/*
* @lc app=leetcode id=560 lang=javascript
*
* [560] Subarray Sum Equals K
*/
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var subarraySum = function (nums, k) {
const hashmap = {};
let acc = 0;
let count = 0;
for (let i = 0; i < nums.length; i++) {
acc += nums[i];
if (acc === k) count++;
if (hashmap[acc - k] !== void 0) {
count += hashmap[acc - k];
}
if (hashmap[acc] === void 0) {
hashmap[acc] = 1;
} else {
hashmap[acc] += 1;
}
}
return count;
};Python Cose
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
d = {}
acc = count = 0
for num in nums:
acc += num
if acc == k:
count += 1
if acc - k in d:
count += d[acc-k]
if acc in d:
d[acc] += 1
else:
d[acc] = 1
return countThere is a similar but a bit more complicated problem. Link to the problem: 437.path-sum-iii(Chinese).