引言
预备知识
深度学习基础
深度学习计算
卷积神经网络
循环神经网络
优化算法
计算性能
计算机视觉
自然语言处理
附录
深度学习库。
MXNet 由 dmlc/cxxnet, dmlc/minerva 和 Purine2 的作者发起,
融合了Minerva 的动态执行,cxxnet 的静态优化和 Purine2 的符号计算等思想,
直接支持基于Python 的 parameter server 接口,使得代码可以很快向分布式进行迁移。
每个模块都进行清晰设计,使得每一部分本身都具有被直接利用的价值。
C 接口和静态/动态 Library 使得对于新语言的扩展更加容易,目前支持C++和python 2/3 ,
接下来相信会有更多语言支持,并方便其他工具增加深度学习功能。
安装依赖:
sudo apt-get update
sudo apt-get install -y build-essential git libatlas-base-dev libopencv-dev
构建MXnet:
git clone --recursive https://github.com/dmlc/mxnet
cd mxnet;
make -j
安装python 接口
进入源码目录编译好的python子目录安装python语言包即可
cd ./python/
sudo python setup.py install
多维的数据结构,提供在 cpu 或者 gpu 上进行矩阵运算和张量计算,
能够自动并行计算
NDArray 是 MXnet 中最底层的计算单元,与 numpy.ndarray 非常相似,
但是也有 2 点不同的特性:
所有的操作可以在不同的设备上运行,包括 cpu 和 gpu。
>>> import mxnet as mx
>>> a = mx.nd.empty((2, 3))
>>> b = mx.nd.empty((2, 3), mx.gpu()) # 在gpu0上创建一个2X3的矩阵
>>> c = mx.nd.empty((2, 3), mx.gpu(2)) # 在gpu2上创建一个2X3的矩阵
>>> c.shape # 维度(2L, 3L)
>>> c.context # 设备信息gpu(2)
##########################
>>> a = mx.nd.zeros((2, 3)) # 创建2X3的全0矩阵
>>> b = mx.nd.ones((2, 3)) # 创建2X3的全1矩阵
>>> b[:] = 2 # 所有元素赋值为2
>>> b = mx.nd.zeros((2, 3), mx.gpu())
>>> a = mx.nd.ones((2, 3)) # 创建2X3的全1矩阵
>>> a.copyto(b) # 从cpu拷贝数据到gpu
###########################################
>>> a = mx.nd.ones((2, 3))
>>> b = a.asnumpy()
>>> type(b)
<type 'numpy.ndarray'>
>>> print b[[ 1. 1. 1.]
[ 1. 1. 1.]]
##########################################
>>> import numpy as np
>>> a = mx.nd.empty((2, 3))
>>> a[:] = np.random.uniform(-0.1, 0.1, a.shape)
>>> print a.asnumpy()[[-0.06821112 -0.03704893 0.06688045]
[ 0.09947646 -0.07700162 0.07681718]]
###########################################
>>> a = mx.nd.ones((2, 3)) * 2
>>> b = mx.nd.ones((2, 3)) * 4
>>> print b.asnumpy()
[[ 4. 4. 4.]
[ 4. 4. 4.]]
>>> c = a + b # 对应元素求和
>>> print c.asnumpy()
[[ 6. 6. 6.]
[ 6. 6. 6.]]
>>> d = a * b # 对应元素求积
>>> print d.asnumpy()
[[ 8. 8. 8.]
[ 8. 8. 8.]]######################################################
>>> a = mx.nd.ones((2, 3)) * 2 ## 默认在CPU上
>>> b = mx.nd.ones((2, 3), mx.gpu()) * 3
>>> c = a.copyto(mx.gpu()) * b
>>> print c.asnumpy()
[[ 6. 6. 6.]
[ 6. 6. 6.]]
#############################################
有两种方法使加载和保存数据变得简单。
第一种是使用pickle,NDArray兼容pickle
>>> import mxnet as mx
>>> import pickle as pkl
>>> a = mx.nd.ones((2, 3)) * 2
>>> data = pkl.dumps(a) ## 导出 存储数据
>>> b = pkl.loads(data) ## 载入 获取数据
>>> print b.asnumpy()
[[ 2. 2. 2.]
[ 2. 2. 2.]]##################################
>>> a = mx.nd.ones((2,3))*2
>>> b = mx.nd.ones((2,3))*3
>>> mx.nd.save('mydata.bin', [a, b]) ## 保存成二进制文件
>>> c = mx.nd.load('mydata.bin') ## 载入二进制文件数据
>>> print c[0].asnumpy() ## c[0] 为a
[[ 2. 2. 2.]
[ 2. 2. 2.]]
>>> print c[1].asnumpy() ## c[1] 为b
[[ 3. 3. 3.]
[ 3. 3. 3.]]
可以导入字典:
>>> mx.nd.save('mydata.bin', {'a':a, 'b':b})
>>> c = mx.nd.load('mydata.bin')
>>> print c['a'].asnumpy()
[[ 2. 2. 2.]
[ 2. 2. 2.]]
>>> print c['b'].asnumpy()
[[ 3. 3. 3.]
[ 3. 3. 3.]]#######################################
>>> mx.nd.save('s3://mybucket/mydata.bin', [a,b])
>>> mx.nd.save('hdfs///users/myname/mydata.bin', [a,b])
###############################################################
#################
不同的操作自动进行并行计算。
a = mx.nd.ones((2,3)) ## 默认cpu上
b = a ## cpu上
c = a.copyto(mx.gpu())## gpu上
a += 1
b *= 3
c *= 3
a += 1 可与
c *= 3 并行计算,因为在不同的设备上,
但是a += 1 和 b *= 3只能相继执行。
以下的范例创建了一个 2 层的感知器网络:
>>> import mxnet as mx
>>> net = mx.symbol.Variable('data')
>>> net = mx.symbol.FullyConnected(data=net, name='fc1', num_hidden=128)##全连接层
>>> net = mx.symbol.Activation(data=net, name='relu1', act_type="relu") ##激活
>>> net = mx.symbol.FullyConnected(data=net, name='fc2', num_hidden=64) ##全连接
>>> net = mx.symbol.SoftmaxOutput(data=net, name='out') ##softmax回归输出层
>>> type(net)
<class 'mxnet.symbol.Symbol'>每一个 Symbol 可以绑定一个名字,Variable 通常用来定义输入,
其他的 Symbol 有一个参数data以一个Symbol 类型作为输入数据,
另外还有其他的超参数num_hidden(隐藏层的神经元数目),act_type(激活函数的类型)。
Symbol 的作用可以被简单的看成是实现了一个函数,函数的参数名称自动生成,可以通过以下的方式查看:
>>> net.list_arguments()
['data', 'fc1_weight', 'fc1_bias', 'fc2_weight', 'fc2_bias', 'out_label']
可以看到,上面的这些参数是每个symbol所需要的输入参数
data:variable data所需要的输入数据
fc1_weight和fc1_bias:是第一全连层fc1所需要的权值和偏执
fc2_weight和fc2_bias:是第二全连层fc2所需要的权值和偏执
out_lable:损失函数的计算出来的标签
>>> net2 = mx.symbol.Variable('data')
>>> w = mx.symbol.Variable('myweight')
>>> net2 = mx.symbol.FullyConnected(data=net2, weight=w, name='fc1', num_hidden=128)
>>> net2.list_arguments()
['data', 'myweight', 'fc1_bias']先在两个symbol之间执行了元素级别的加法,然后将加的结果反馈到了fully connected operator
>>> lhs = mx.symbol.Variable('data1')
>>> rhs = mx.symbol.Variable('data2')
>>> net = mx.symbol.FullyConnected(data=lhs + rhs, name='fc1', num_hidden=128)
>>> net.list_arguments()
['data1', 'data2', 'fc1_weight', 'fc1_bias']>>> net = mx.symbol.Variable('data')
>>> net = mx.symbol.FullyConnected(data=net, name='fc1', num_hidden=128)
>>> net2 = mx.symbol.Variable('data2')
>>> net2 = mx.symbol.FullyConnected(data=net2, name='net2', num_hidden=128)
>>> composed_net = net(data=net2, name='compose')
>>> composed_net.list_arguments()
['data2', 'net2_weight', 'net2_bias', 'compose_fc1_weight', 'compose_fc1_bias']在上面的例子中,net作为一个函数应用于一个已经存在的symbol net,
他们的结果composed_net将会替换原始的参数data net2.
>>> net = mx.symbol.Variable('data')
>>> net = mx.symbol.FullyConnected(data=net, name='fc1', num_hidden=10)
>>> arg_shape, out_shape, aux_shape = net.infer_shape(data=(100, 100))
>>> dict(zip(net.list_arguments(), arg_shape))
{'data': (100, 100), 'fc1_weight': (10, 100), 'fc1_bias': (10,)}
>>> out_shape
[(100, 10)]>>> # 定义计算图
>>> A = mx.symbol.Variable('A')
>>> B = mx.symbol.Variable('B')
>>> C = A * B
>>> a = mx.nd.ones(3) * 4
>>> b = mx.nd.ones(3) * 2
>>> # 绑定变量到Symbol
>>> c_exec = C.bind(ctx=mx.cpu(), args={'A' : a, 'B': b})
>>> # 进行前向计算
>>> c_exec.forward()
>>> c_exec.outputs[0].asnumpy()
[ 8. 8. 8.]对于神经网络而言,一个更加常用的形式是simple_bind,将会为你创建所有的参数数组。
然后你调用forward和backward来获取梯度。
>>> # 定义计算流图
>>> net = some symbol
>>> texec = net.simple_bind(data=input_shape)
>>> texec.forward()
>>> texec.backward()KVStore 实现了在多个运算器之间,或者在多台计算机之间的数据同步
MXNet提供一个分布式的key-value存储来进行数据交换。它主要有两个函数,
push: 将key-value对从一个设备push进存储
pull:将某个key上的值从存储中pull出来此外,
KVStore还接受自定义的更新函数来控制收到的值如何写入到存储中。
最后KVStore提供数种包含最终一致性模型和顺序一致性模型在内的数据一致性模型。
分布式梯度下降算法:
KVStore kvstore("dist_async");
kvstore.set_updater([](NDArray weight, NDArray gradient) {
weight -= eta * gradient;
});
for (int i = 0; i < max_iter; ++i) {
kvstore.pull(network.weight);
network.forward();
network.backward();
kvstore.push(network.gradient);
}在这里先使用最终一致性模型创建一个kvstore,然后将更新函数注册进去。
在每轮迭代前,每个计算节点先将最新的权重pull回来,之后将计算的得到的梯度push出去。
kvstore将会利用更新函数来使用收到的梯度更新其所存储的权重。
在store里面初始化一个(int, NDArray)对,然后将这个值pull拉出去。
>>> kv = mx.kv.create('local') # 创建一个本地的kvstore
>>> shape = (2,3)
>>> kv.init(3, mx.nd.ones(shape)*2)
>>> a = mx.nd.zeros(shape)
>>> kv.pull(3, out = a)
>>> print a.asnumpy()
[[ 2. 2. 2.]
[ 2. 2. 2.]]对于任何已经被初始化的key值,我们可以push一个新的相同大小的值。
>>> kv.push(3, mx.nd.ones(shape)*8) ##推入
>>> kv.pull(3, out = a) # 取出值
>>> print a.asnumpy()
[[ 8. 8. 8.]
[ 8. 8. 8.]]>>> gpus = [mx.gpu(i) for i in range(4)]
>>> b = [mx.nd.ones(shape, gpu) for gpu in gpus]## 四个gpu上分别存储[[ 1. 1. 1.] [ 1. 1. 1.]]
>>> kv.push(3, b)
>>> kv.pull(3, out = a)##push聚合求后的值
>>> print a.asnumpy()
[[ 4. 4. 4.]
[ 4. 4. 4.]]对每次push,KVStore使用updater将push的值和存储的值加起来。
默认的updater是ASSIGN,我们可以替换默认的来控制怎样融合数据
>>> def update(key, input, stored):
>>> print "update on key: %d" % key
>>> stored += input * 2
>>> kv._set_updater(update) ##更新KVStore的updater
>>> kv.pull(3, out=a)
>>> print a.asnumpy()
[[ 4. 4. 4.]
[ 4. 4. 4.]]
>>> kv.push(3, mx.nd.ones(shape))
update on key: 3
>>> kv.pull(3, out=a)
>>> print a.asnumpy()
[[ 6. 6. 6.]
[ 6. 6. 6.]]>>> b = [mx.nd.ones(shape, gpu) for gpu in gpus]
>>> kv.pull(3, out = b)
>>> print b[1].asnumpy()
[[ 6. 6. 6.]
[ 6. 6. 6.]]>>> keys = [5, 7, 9]
>>> kv.init(keys, [mx.nd.ones(shape)]*len(keys))
>>> kv.push(keys, [mx.nd.ones(shape)]*len(keys))
update on key: 5
update on key: 7
update on key: 9
>>> b = [mx.nd.zeros(shape)]*len(keys)
>>> kv.pull(keys, out = b)
>>> print b[1].asnumpy()
[[ 3. 3. 3.]
[ 3. 3. 3.]]>>> b = [[mx.nd.ones(shape, gpu) for gpu in gpus]] * len(keys)
>>> kv.push(keys, b)
update on key: 5
update on key: 7
update on key: 9
>>> kv.pull(keys, out = b)
>>> print b[1][1].asnumpy()
[[ 11. 11. 11.]
[ 11. 11. 11.]]##################################
如何在MXNet上写一个分布式程序
MXNet提供了一个分布式key-value store名为kvstore减少了数据同步操作的复杂性。
它提供了以下的功能:
push:将本地数据push到分布式存储,如梯度等
pull:将数据从分布式存储中pull过来,如新的权值
set_updater:为分布式存储设置一个updater,明确store是如何将接收到的数据进行融合的,
例如:怎样使用接收到的梯度来更新权值。
如果你的程序按照下面的结构写的,事情会更加简单:
data = mx.io.ImageRecordIter(...)
net = mx.symbol.SoftmaxOutput(...)
model = mx.model.FeedForward.create(symbol = net, X = data, ...)上面的数据是取自于一个image record iterator,并使用一个符号化网络进行模型训练。
为了将它扩展成一个分布式的程序,首先要建立一个kvstore,
然后将它传入到create函数中。
下面的程序将上面的SGD修改成了分布式异步的SGD:
data = mx.io.ImageRecordIter(...)
net = mx.symbol.SoftmaxOutput(...)
kv = mx.kvstore.create('dist_sync')
model = mx.model.FeedForward.create(symbol = net, X = data, kvstore = kv, ...)######################################
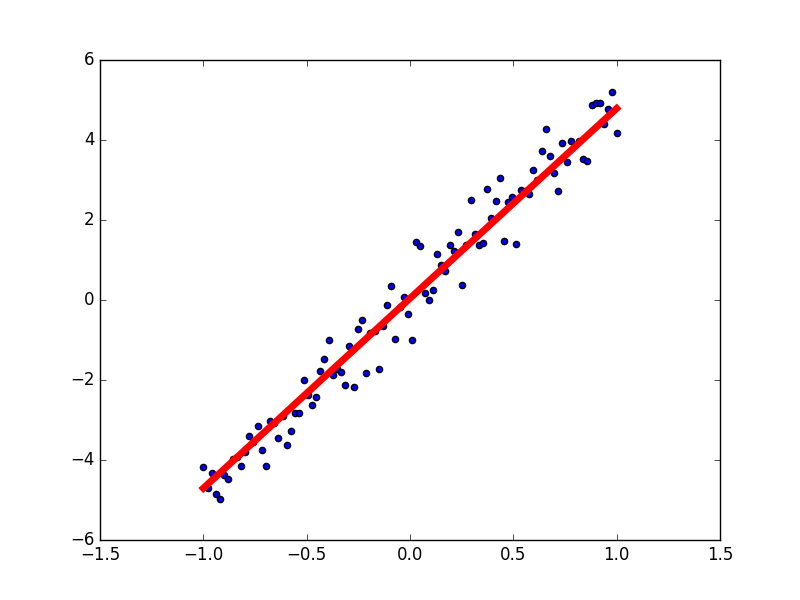
以下借助 MXnet 实现了一个简单的单变量线性回归程序:
import mxnet as mx
import numpy as np
import matplotlib.pyplot as plt
# 定义输入数据
X_data = np.linspace(-1, 1, 100)
noise = np.random.normal(0, 0.5, 100)
y_data = 5 * X_data + noise
# Plot 输入数据
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(X_data, y_data)
# 定义mxnet变量
X = mx.symbol.Variable('data')
Y = mx.symbol.Variable('softmax_label')
# 定义网络
Y_ = mx.symbol.FullyConnected(data=X, num_hidden=1, name='pre')
loss = mx.symbol.LinearRegressionOutput(data=Y_, label=Y, name='loss')
# 定义模型
model = mx.model.FeedForward(
ctx=mx.cpu(),
symbol=loss,
num_epoch=100,
learning_rate=0.001,
numpy_batch_size=1
)
# 训练模型
model.fit(X=X_data, y=y_data)
# 预测
prediction = model.predict(X_data)
lines = ax.plot(X_data, prediction, 'r-', lw=5)
plt.show()