Skip to content

Latest commit

 

History

History
128 lines (79 loc) · 5.12 KB

b_tree.md

File metadata and controls

128 lines (79 loc) · 5.12 KB

B-Tree

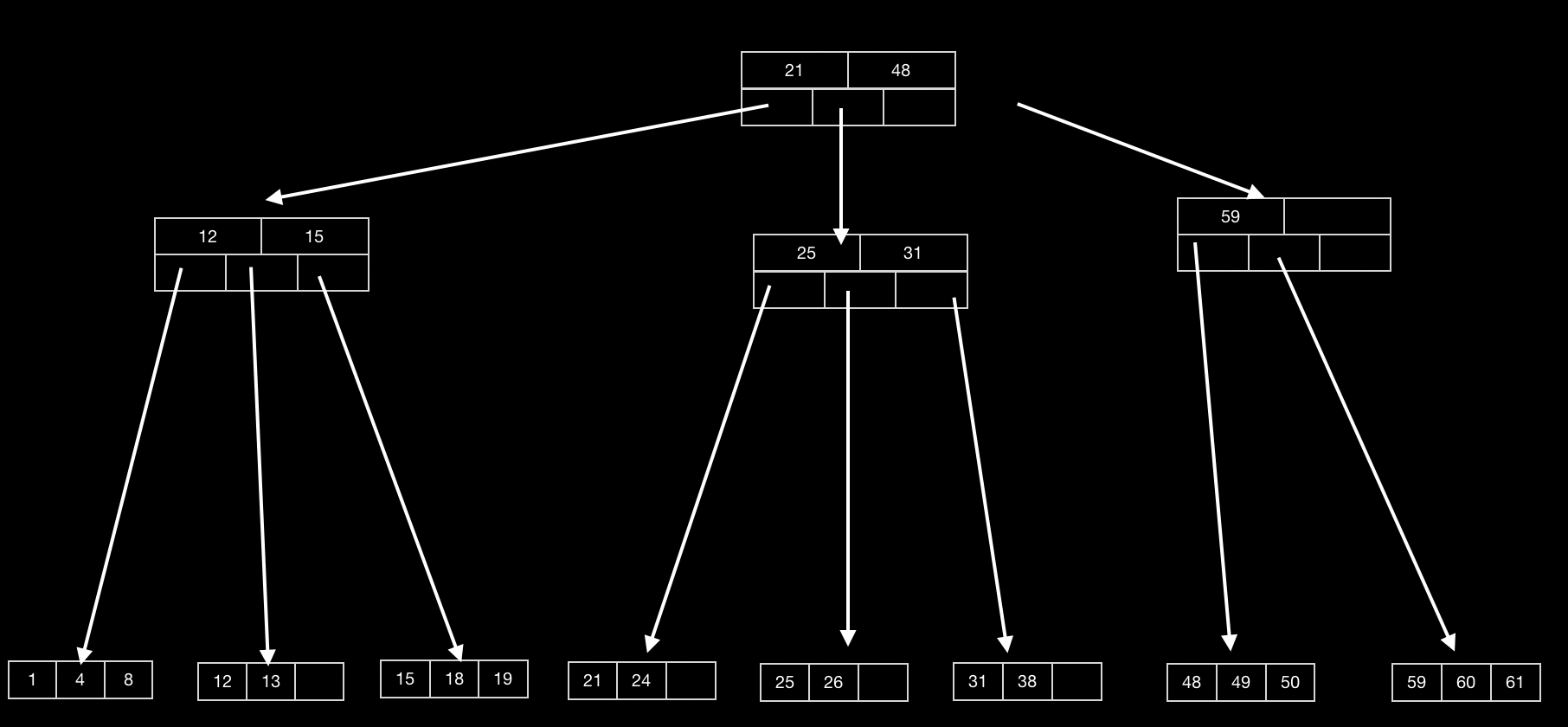
之前看到的都是二叉树，还有一种常见的树，b-tree,M阶B树，它有以下特点

  1. 树的根节点是一个叶子节点或者其儿子节点的数量在2到M之间
  2. 除根节外，其它所有非叶子节点儿子在[M/2]和M之前。
  3. 非根叶子节点中的关键词数量在[M/2]和M之前
  4. 所有的叶子节点都有相同的深度
  5. 每个节点的儿子节点都是有序的
  6. 每个叶子节点最多有M个数据

它是一种多路平衡树，和它的变种B+树主要应用在数据库方面。

比较常见的有4阶B树(2-3-4树),以及3阶B树(2-3)树

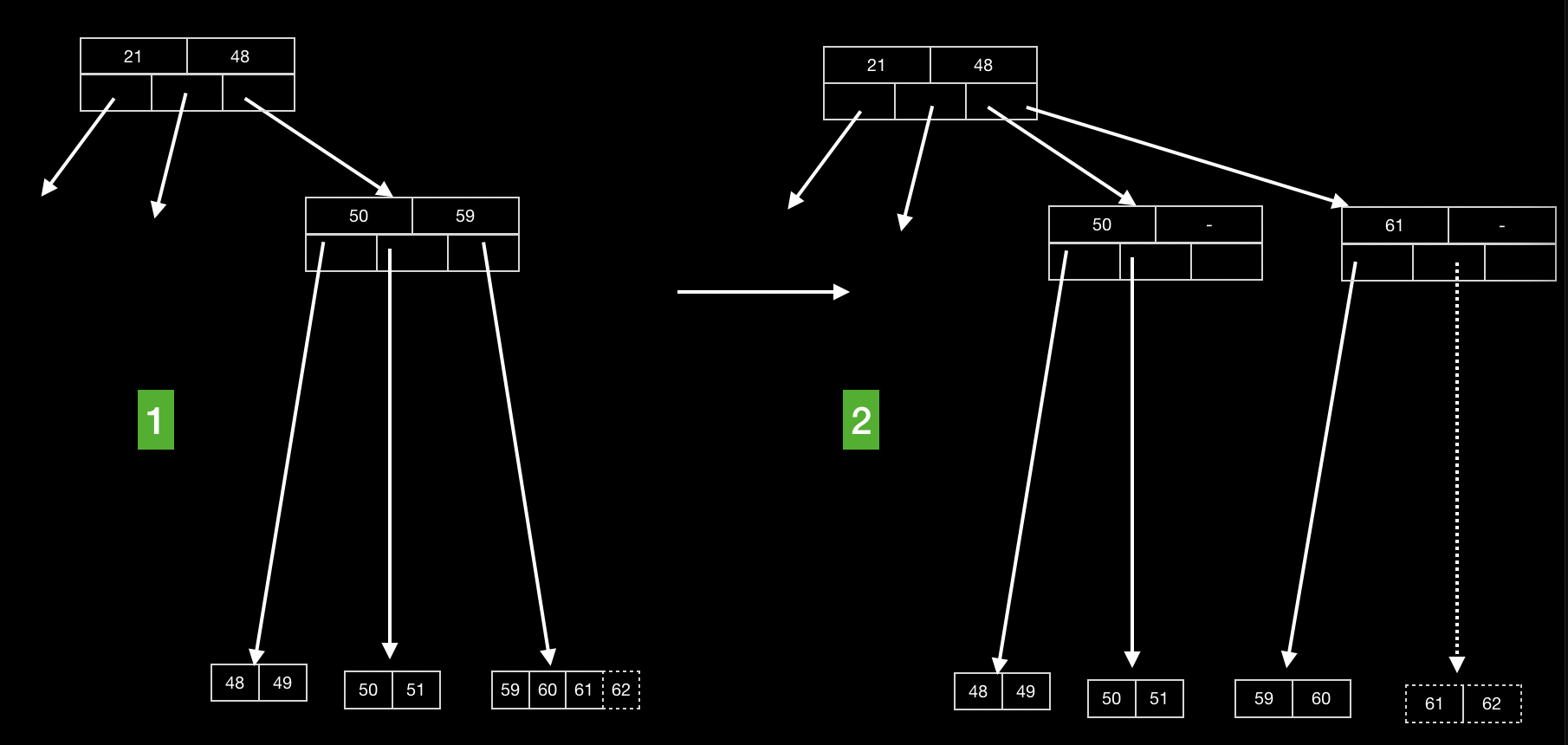
下面以3阶为例(其叶子节点的关键词个数2-3个)，看一下它的一些常见的操作过程.

插入

  1. 插入节点 14: 此时刚好空间足够，无需更改结构

  2. 然后插入节点 51,但是此时，该关键词所在的叶子节点容量以达到最大，此时需要进行拆分。 将该节点拆分程两个叶子节点

  3. 然后插入关键字62，此时该关键字所在的节点以达到最大容量，同时其上层节点的容量也到达最大，此时要进行逐层分裂，直到每个节点都满足条件位置

其实能够看到，分裂过程中，对应分割关键词取其右子树的最小值即可。

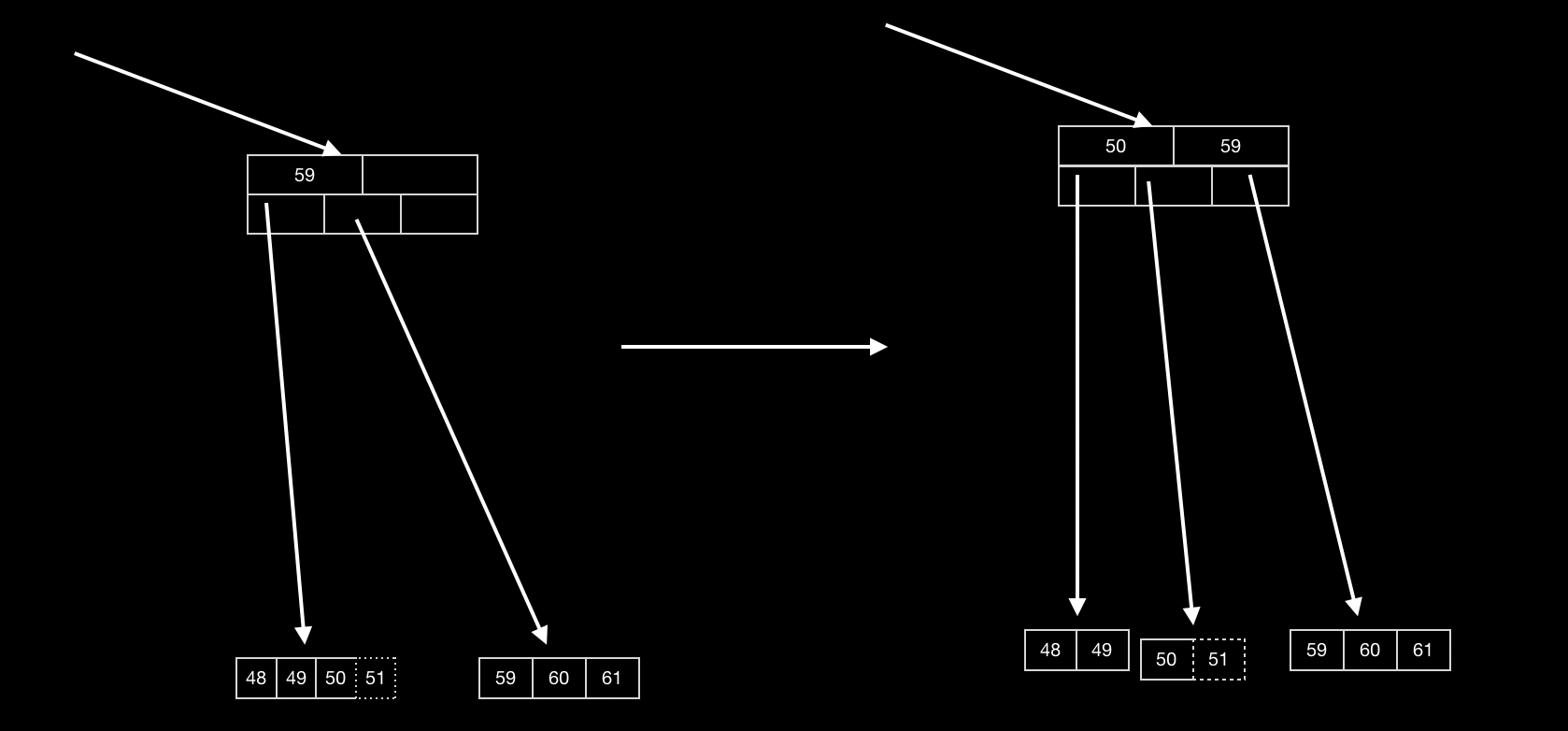
还有，再插入的时候，按照如上方式得到的子节点数量可能太多，可以先找其对应空间不满的兄弟节点，进行合并，调整节点即可，无需在进行分裂。

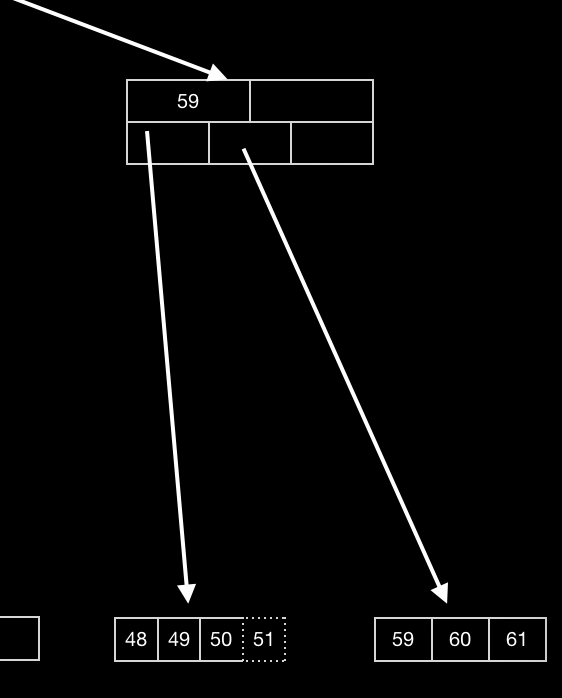
例如，在插入关键词62时，可以修改为如下 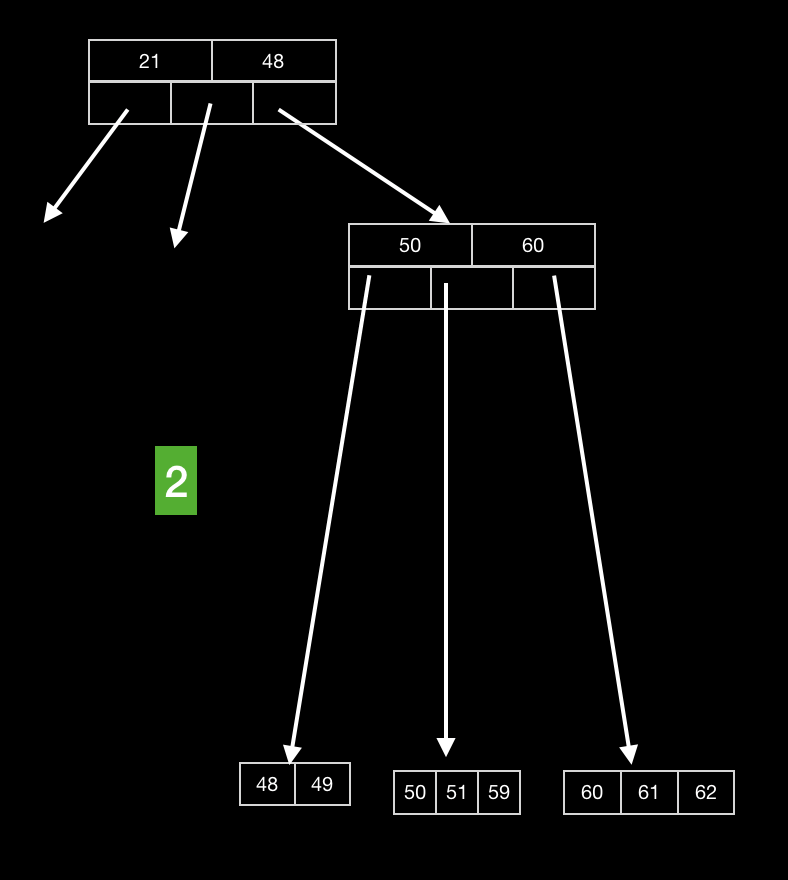这样可以无需大量调整树的节点，而且节省空间

删除

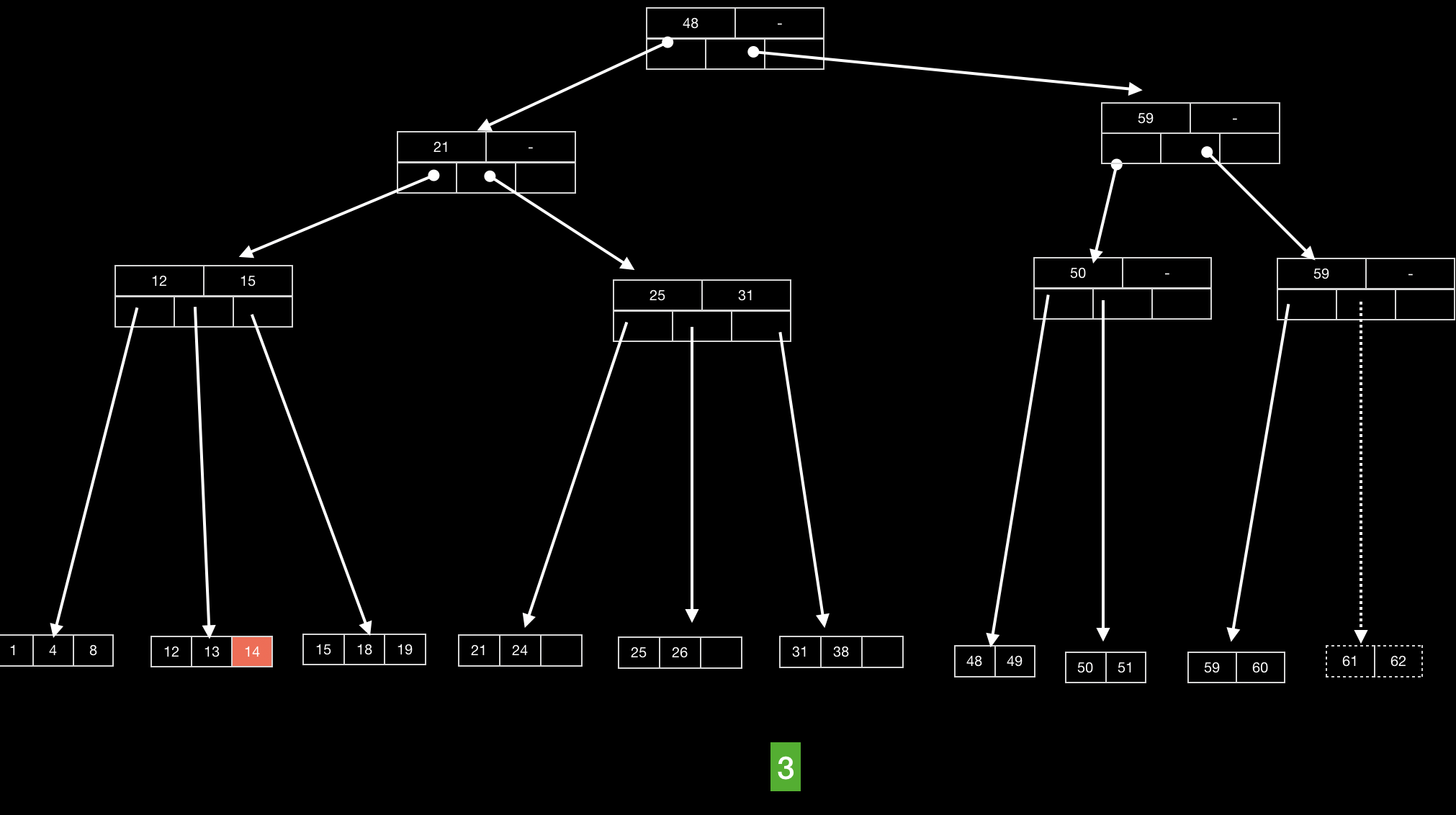
删除其实也是对叶子节点的删除，但是它分为几种情况

  1. 该关键词所在的叶子节点关键词数量为2
  2. 该关键词所在的叶子节点关键词数量大于2

以下图为例

该关键词所在的叶子节点关键词数量为2

因为要求叶子节点中兄弟节点含有超过两个关键词的节点，可以将其拿出一个，使其保持数量为2 如果兄弟节点的关键词数量，都是2，那么将两个节点合并即可。 同时，向上调整，查看对应父节点是否符合要求

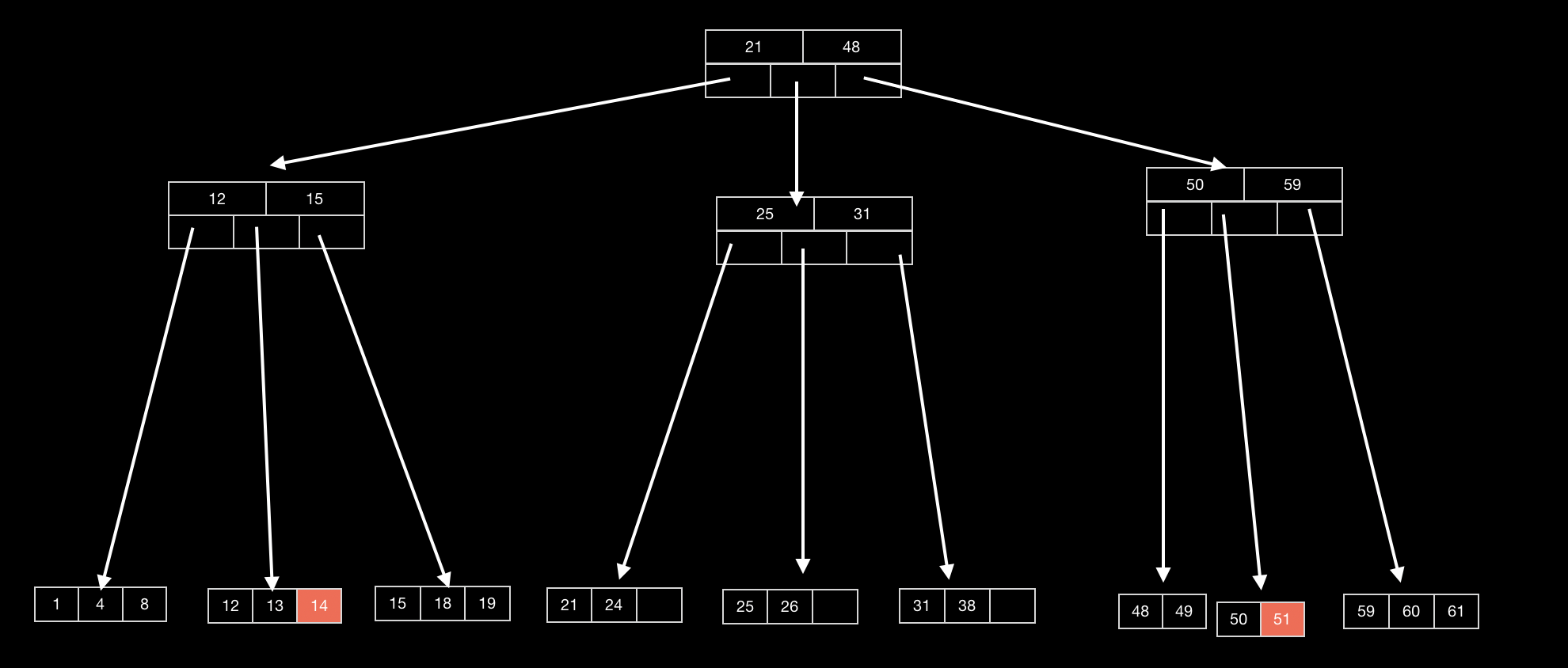
删除关键词25

由于25所在的叶子节点关键词个数为2,那么删除完毕后，只剩余1个关键词，不符合要求。同时，它的兄弟节点，存在关键词为2的节点，此时将其两个合并，同时向上调整节点。 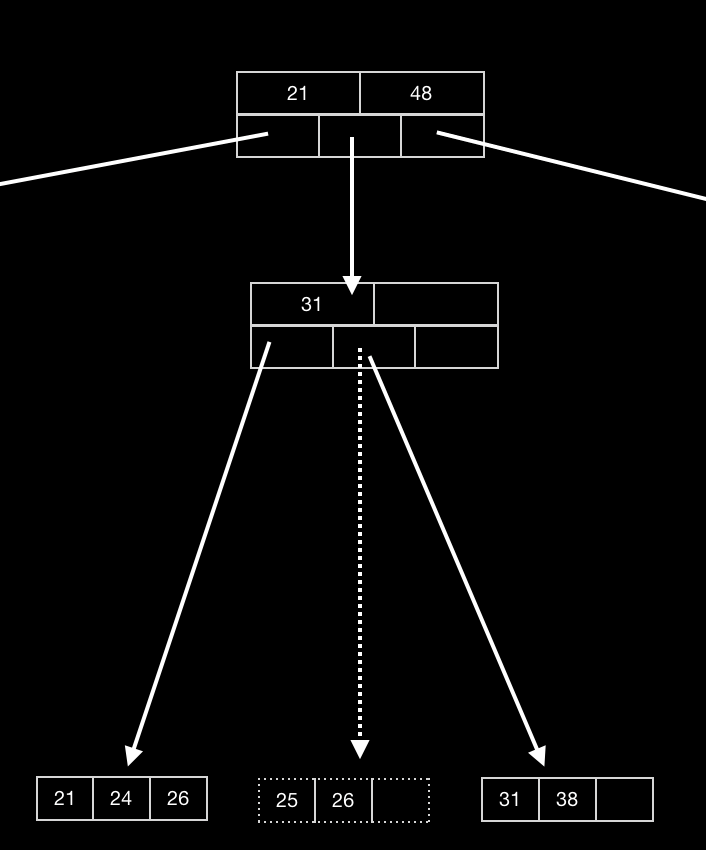这里可以固定为与它最近的一个兄弟节点(从小到大)，该节点若关键词超过2，则拿出一个，否则，合并

该关键词所在的叶子节点关键词数量大于2

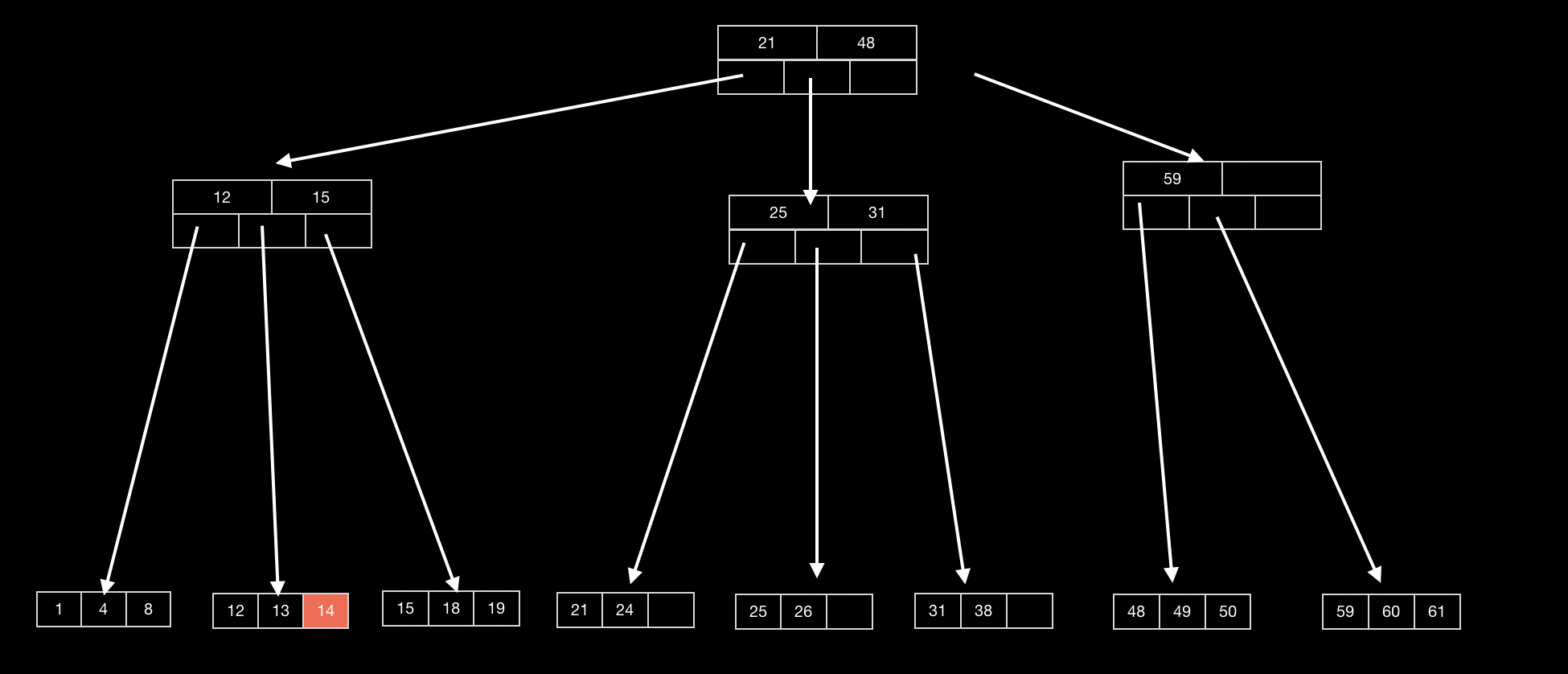
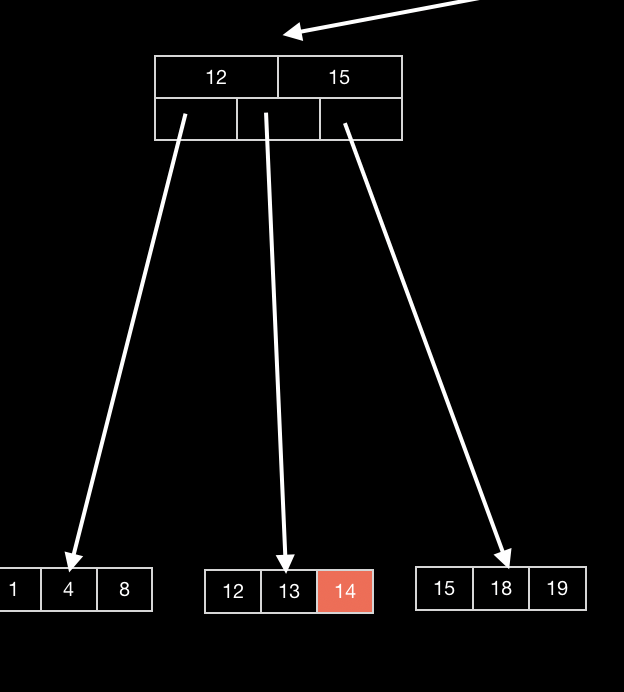
这种情况，符合叶子节点关键词数量的最低要求，直接删除即可。

删除节点14。只需直接删掉即可

实现

数据结构

从定义和流程上，综合考虑，它的节点应该满足以下性质

  1. 每个节点都具有以下属性
    1. 当前节点的关键词个数 num
    2. num 个关键词构成的集合，且集合中的元素应当与非降序排列的
    3. leaf 一个布尔类型，来判断是否为叶子节点
  2. 每个节点应当还存储在各个子树上的关键词加以分割
struct BTreeNode
{
    int num; // the value num in this node
    struct BTreeNode *ptr[M+1]; // the ptr collection + 1 
    Element *elements[M+1]; // the value collection + 1 
    boolean isLeaf;               // is leaf or not
};

其中:

  1. num代表该节点拥有的关键词个数
  2. M是指树的阶数
  3. M+1是为了在调整过程中更加方便
  4. ptr 是一个指针数组，指向它的孩子节点
  5. elements代表为关键词
  6. 是否为叶子节点

因为，一旦定义了阶数，关键词和指针的最大数量就可以唯一确定了，所以采用数组更加合理，而且可以高效的访问，删除只需要将固定索引的指针和值置为NULL

B and B+ tree

B+ 树相对于 B 树稍微有所区别，B+ 树的所有关键词存储在 叶节点上，且叶子节点构成一个链表。 非叶子节点，只做索引。

B+ 树相见 b_plus_tree

Reference

  1. the linux b-tree filesystem
  2. the ubiquitous b-tree
  3. 数据结构与算法分析
  4. 算法导论