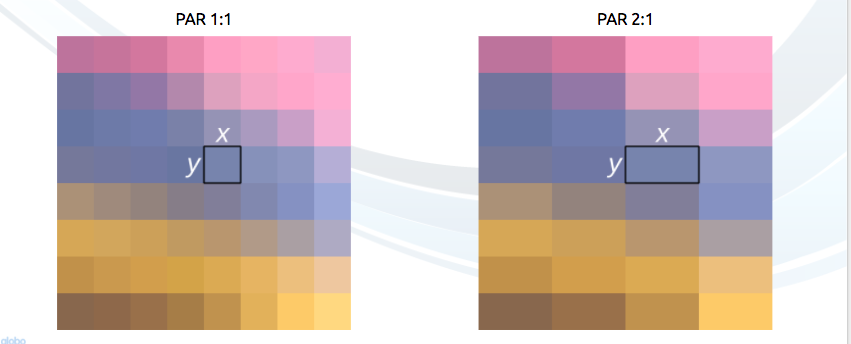Skip to content

coog009/digital_video_introduction

BranchesTags

Repository files navigation

license

Intro

This text will be used to provide a gentle introduction to video technology, although it's aimed to software developers / engineering we want to make it easy for anyone to learn.

The idea is to introduce some video subjects with an ease to understand text (at least for developers), visual element and practical examples where is possible. Also, feel free to send error corrections, suggestions, grammar fixes, and etc via PRs.

There will be hands-on sections which requires you to have docker installed and this repo cloned.

git clone https://github.com/leandromoreira/introduction_video_technology.git
cd introduction_video_technology
./setup.sh

All the hands-on should be performed from the folder you cloned this repository, for the jupyter examples you must start the server ./s/start_jupyter.sh and follow the instructions.

Index

Basic video/image terminology

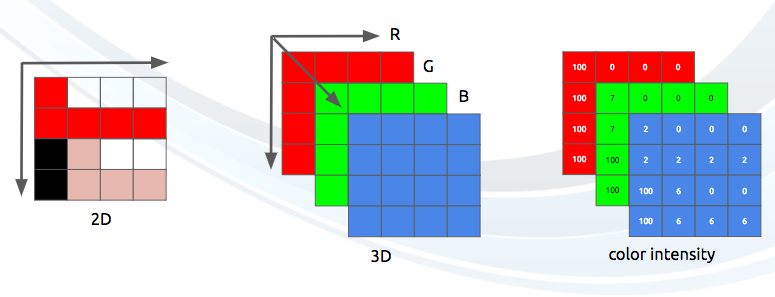
An image can be thought as a 2D matrix and if we think about colors, we can extrapolate this idea seeing this image as a 3D matrix where the additional dimensions are used to provide color info.

If we chose to represent these colors using the primary colors (red, green and blue), we then can define the tree planes: the first one red, the second green and the last the blue color.

an image is a 3d matrix RGB

Each point in this matrix, we'll call it a pixel (picture element), will hold the intensity (usually a numeric value) of that given color. A total red color means 0 of green, 0 of blue and max of red, the pink color can be formed with (using 0 to 255 as the possible range) with Red=255, Green=192 and Blue=203.

Other ways to encode a color image

There are much more models to represent an image with colors. We could use a indexed palette where we'd spend only a byte for each pixel instead of 3, comparing it to RGB model. In this model instead of a 3D matrix we'd use a 2D matrix, saving memory but having much less color options.

NES palette

For instance, look at the first Super Mario's picture down bellow, we can see that it has a lots of red and few blue colors therefore the red color will be the one that contributes more (the brightest parts) to the final color while the blue color contribution can be mostly only seen in Mario's eyes and part of his clothes.

RGB channels intensity

And each color intensity requires a certain amount of bits, this quantity is know as bit depth. Let's say we spend 8 bits (accepting values from 0 to 255) per color (plane), therefore we have a color depth of 24 (8 * 3) bits and we can also infer that we could use 2 to the power of 24 different colors.

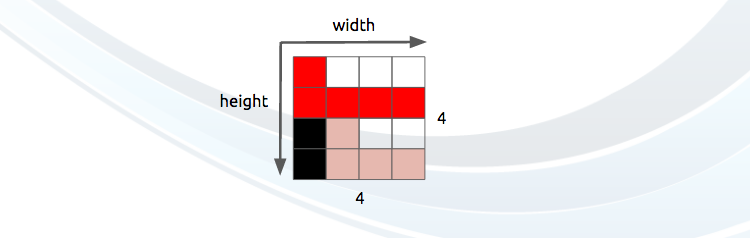
An image has also another property such as resolution which is the number of pixels in each dimension. It is often presented as width × height, for example the 4×4 image bellow.

image resolution

Hands-on: play around with image and color

You can play around with image and colors using jupyter (python, numpy, matplotlib and etc).

You can also learn how image filters (edge detection, sharpen, blur...) work.

Another property we can see while working with images or video is aspect ratio which is simple describes the proportional relationship between width and height of an image or pixel.

When people says this movie or picture is 16x9 they usually are referring to the Display Aspect Ratio (DAR) and we also can have different shapes of a pixel, we call this Pixel Aspect Ratio (PAR).

display aspect ratio

pixel aspect ratio

DVD is DAR 4:3

Although the real resolution of a DVD is 704x480 it still keeps a 4:3 aspect ratio because it has a PAR of 10:11 (704x10/480x11)

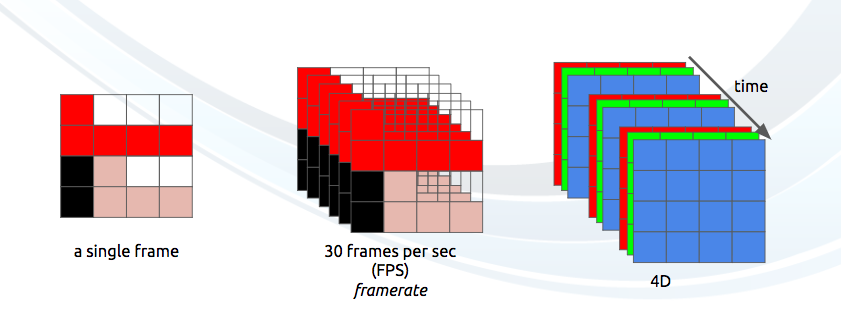
Finally we can define a video as a succession of n frames in time which can be seen as another dimension, n is the frame rate or frames per second(FPS).

video

The amount of bits per second needed to show a video is its bit rate. For example, a video with 30 frames per second, 24 bits per pixel, resolution of 480x240 will need 82,944,000 bits per second or 82.944 Mbps (30x480x240x24) if we don't employ any kind of compression.

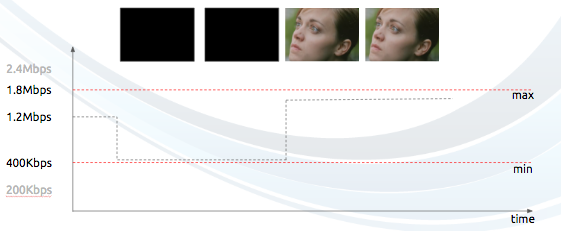
When the bit rate is constant it's called constant bit rate (CBR) but it also can vary then called variable bit rate (VBR).

constrained vbr

In the early days engineering come up with a technique for doubling the perceived frame rate of a video display without consuming extra bandwidth, this technique is known as interlaced video. It basically sends half of the screen in 1 "frame" and the next "frame" they send the other half.

Today screens render mostly using progressive scan technique, progressive is a way of displaying, storing, or transmitting moving images in which all the lines of each frame are drawn in sequence.

interlaced vs progressive

Now we have an idea about what is an image, how its colors are arranged, how many bits per second do we spend to show a video, if it's constant (CBR) or variable (VBR), with a given resolution using a given frame rate and many other terms such as interlaced, PAR and others.

Hands-on: Check video properties

You can check most of the explained properties with ffmpeg or mediainfo.

Image capture

[WIP]

Redundancy removal

[WIP]

How does a video codec work?

[WIP]

A little bit of the past and present

Past

Present (AV1 vs HEVC)

1st step - picture partitioning

2nd step - predictions

3rd step - transform

4th step - quantization

5th step - entropy coding

After we quantized the data (image blocks/slices/frames) we still can compress it in a lossless way. There are many ways (algorithms) to compress data. We're going to briefly experience some of them, for a deeper understanding you can read the amazing book Understanding Compression: Data Compression for Modern Developers.

Delta coding:

I love the simplicity of this method (it's amazing), let's say we need to compress the following numbers [0,1,2,3,4,5,6,7] and if we just decrease the current number to its previous and we'll get the [0,1,1,1,1,1,1,1] array which is highly compressible.

Both encoder and decoder must know the rule of delta formation.

VLC coding:

Let's suppose we have a stream with the symbols: a, e, r and t and their probability (from 0 to 1) is represented by this table.

a e r t
probability 0.3 0.3 0.2 0.2

We can assign unique binary codes (preferable small) to the most probable and bigger codes to the least probable ones.

a e r t
probability 0.3 0.3 0.2 0.2
binary code 0 10 110 1110

Let's compress the stream eat, assuming we would spend 8 bits for each symbol, we would spend 24 bits without any compression. But in case we replace each symbol for its code we can save space.

The first step is to encode the symbol e which is 10 and the second symbol is a which is added (not in the mathematical way) [10][0] and finally the third symbol t which makes our final compressed bitstream to be [10][0][1110] or 1001110 which only requires 7 bits (3.4 times less space than the original).

Notice that each code must be a unique prefixed code Huffman can help you to find these numbers. Though it has some issues there are video codecs that still offers this method and it's the algorithm for many application which requires compression.

Both encoder and decoder must know the symbol table with its code therefore you need to send the table too.

Arithmetic coding:

Let's suppose we have a stream with the symbols: a, e, r, s and t and their probability is represented by this table.

a e r s t
probability 0.3 0.3 0.15 0.05 0.2

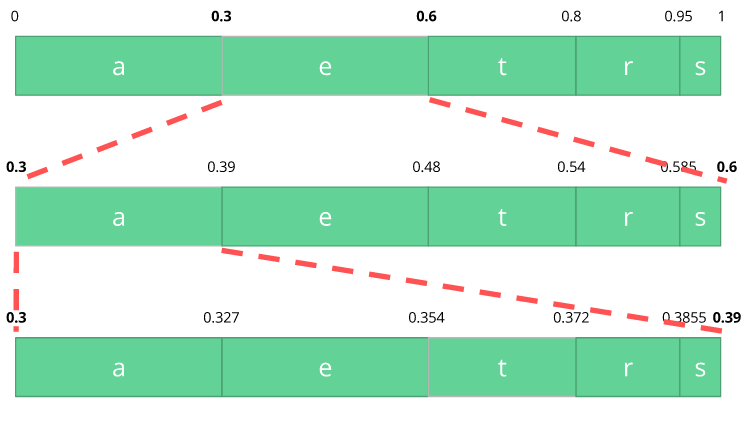
With this table in mind we can build ranges containing all the possible symbols sorted by the most frequents.

initial arithmetic range

Now let's encode the stream eat, we pick the first symbol e which is located within the subrange 0.3 to 0.6 (but not included) and we take this subrange and split it again using the same proportions used before but within this new range.

second sub range

Let's continue to encode our stream eat, now we take the second symbol a which is within the new subrange 0.3 to 0.39 and then we take our last symbol t and we do the same process again and we get the last subrange 0.354 to 0.372.

final arithmetic range

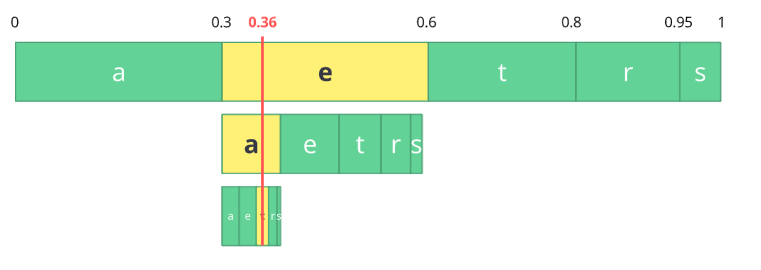
We just need to pick a number within the last subrange 0.354 to 0.372, let's chose 0.36 but we could chose any number within this subrange. With only this number we'll be able to recovery our original stream eat. If you think about it, it's like if we were drawing a line within ranges of ranges to encode our stream.

final range traverse

The reverse process (A.K.A. decoding) is equally easy, with our number 0.36 and our original range we can run the same process but now using this number to reveal the stream encoded behind this number.

With the first range we notice that our number fits at the e slice therefore it's our first symbol, now we split this subrange again, doing the same process as before, and we'll notice that 0.36 fits the symbol a and after we repeat the process we came to the last symbol t (forming our original encoded stream eat).

Both encoder and decoder must know the symbol probability table, therefore you need to send the table.

Pretty neat isn't? People are damm smart to come up with such solution, some video codec uses (or at least offers as an option) this technique.

The idea is to lossless compress the quantized bitstream, for sure this article is missing tons of details, reasons, trade-offs and etc. But you should learn more as a developer.

Hands-on: CABAC vs CAVLC

You can generate two streams, one with CABAC and other with CAVLC and compare the time it took to generate each of them as well as the final size.

6th step - bitstream format

After we did all these steps we need to pack all these bits and its meanings. We need to explicitly inform the encoder about the decisions done by encoder, things like bit depth, color space, resolution, predictions info, profile, level, frame rate and etc.

Hands-on: Inspect the H264 bitstream

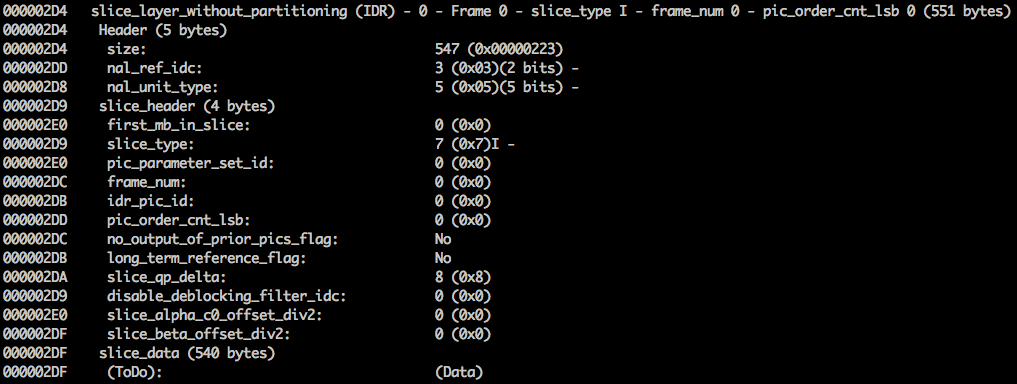
We can generate a single frame video and use mediainfo to inspect its H264 bitstream. In fact, you can even see the source code that parses h264 (AVC) bitstream.

mediainfo details h264 bitstream

We can also use the Intel Video Pro Analyzer which is paid but there is a free trial version which limits you to only the first 10 frames but that's okay for learning purposes.

intel video pro analyzer details h264 bitstream

How H265 can achieve better compression ratio than H264

[WIP]

Adaptive streaming

[WIP]

Encoding parameters the whys

[WIP]

Audio codec

[WIP]

How to use jupyter

Make sure you have docker installed and just run ./s/start_jupyter.sh and follow the instructions on the terminal.

References

The richest content is here, where all the info we saw in this text was extracted, based or inspired by. You can deepen your knowledge with these amazing links, books, videos and etc.

About

A hands-on introduction to video technology: image, video, codec (av1, vp9, h265) and more (ffmpeg encoding).

github.com/leandromoreira/introduction_video_technology

Resources

Readme

License

BSD-3-Clause license

Code of conduct

Code of conduct
Activity

Stars

0 stars

Watchers

2 watching

Forks

0 forks
Report repository

Releases

2 tags

Packages

No packages published

Languages

  • Jupyter Notebook 99.9%
  • Shell 0.1%