Table of Contents
- Pairwise Set Reconciliation Protocol
- FPTree Data Structure
- Multi-peer Reconciliation
The recursive set reconciliation protocol described in this section is based on Range-Based Set Reconciliation paper by Aljoscha Meyer.
The set reconciliation protocol is intended to synchronize ordered sets. An orrered set provides possibility to compare its elements, and consequently, elements can be retrieved in order from the set. Formally, the kind of ordered sets syncv2 can synchronize is called totally ordered sets.
The elements of the sets are actually keys, hash-based IDs of actual entities such as ATXs. The actual entities are transferred separately after the sets have been synchronized.
Range specifies continuous subranges in the ordered set with defined bounds. The algorithm works by recursively subdividing the ordered set into ranges, for which fingerprints are calculated.
Fingerprint is used to check if the range with the same bounds contains the same elements in two sets belonging to different peers. If fingerprint of a range is the same for both peers, their sets are considered equal. The fingerprints are calculated by XORing together the elements (keys) in the set.
The set reconciler uses an optimized data structure that makes
fingerprint calculations cost O(log n) under most circumstances.
It will be discussed separately.
Synchronization of ordered sets is done using range fingerprints and an interactive stateless protocol.
The latter means that response(s) to each message, if any, are generated solely based on that message and the local set and not based on any previous messages. The exception to that rule is Done and EndRound messages (see corresponding sections below).
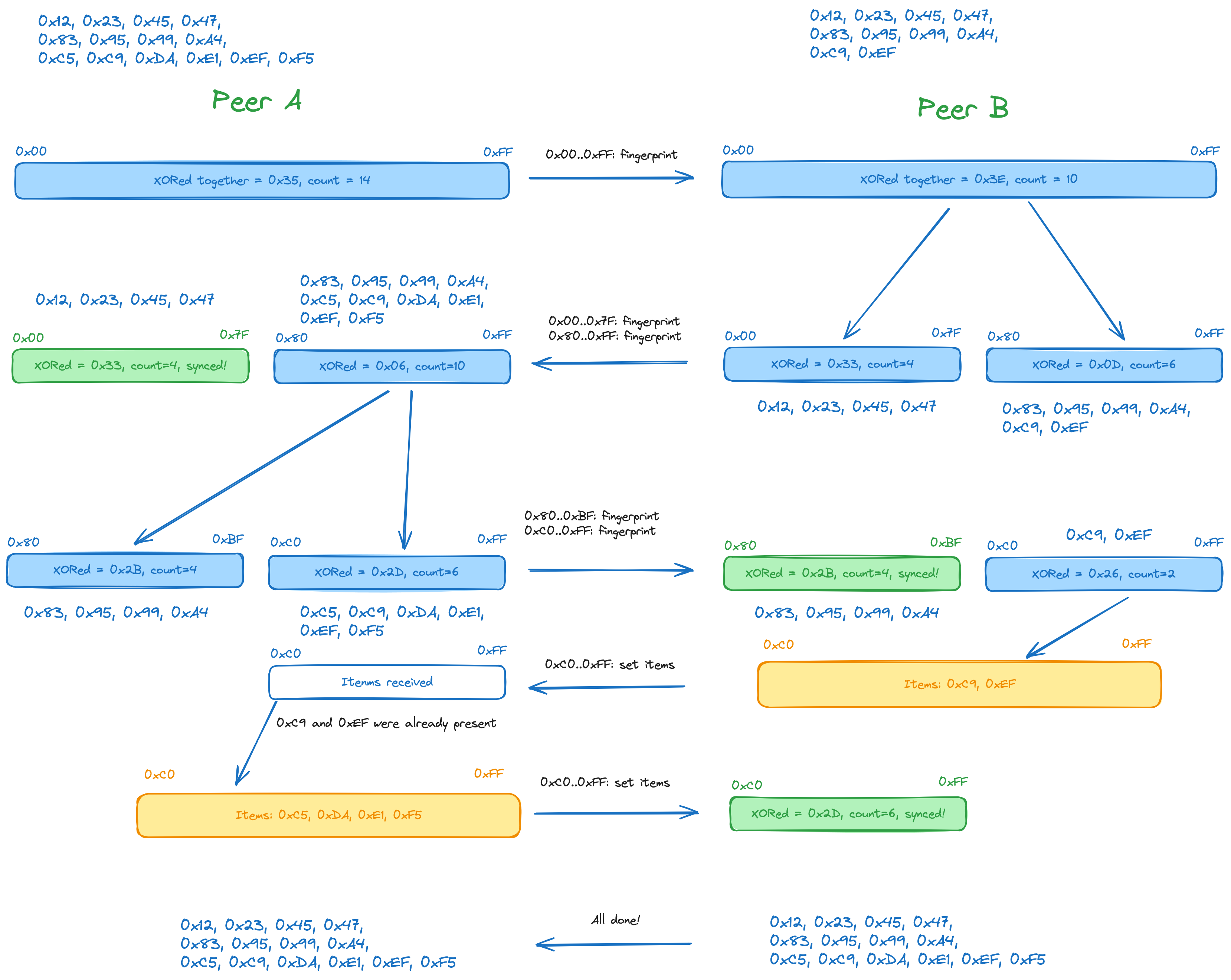
Below is an illustration of simplified reconciliation between two sets. Let's assume that the items are mere bytes, fingerprints being these bytes XORed together.
The range representation used for this example is simplified, with proper range representation being discussed in following sections. For now, let's just describe ranges using inclusive notation, 0x00..0xff meaning all the values from 0x00 up to and including 0xff.
- Initially, the fingerprint of the whole set is sent from A to B.
- Checking the fingerprint of its set, B finds out that A has a different fingerprint, and thus splits the whole range of elements in two subranges, calculating fingerprints for them and sending these fingerprints back to A.
- A finds out that the fingerprint for the 0x00..0x7f subrange, 0x33, is the same as the fingerprint received for the same subrange from B; thus, 0x00..0x7f subrange is considered synchronized and no response is sent back.
- The 0x80..0xff range, on the other hand, has different fingerprints on A and B side. Because of that, A recursively subdivides the 0x80..0xff range into 0x80..0xbf and 0xc0..0xff ranges, calculates the fingerprints of these new ranges and sends the range boundaries together with the fingerprints to B.
- B notices that the fingerprint for 0x80..0xbf is the same on its side, so 0x80..0xbf range is considered synchronized.
- The subrange 0xc0..0xff has a different fingerprint on the B side, but the number of elements in it (2) is small enough, so instead of further subdivision we can just send all the items in that range to A, together with the range boundaries.
- Having received the items for the 0xc0..0xff range, A sends all the elements it has that fall within that range back to B.
- At this point, the sets are considered to be in sync.
The following is done to mitigate possible attacks against set reconciliation algorithm:
- do not distribute freshly synced data before validation
- drop peers that provide data that can't pass validation, or do not provide the actual entities after sending their IDs. This in particular makes it much harder to forge invalid IDs that may cause fingerprint collisions
- limit the number of messages and the amount of data transferred
Later, we may also add some more checks, such as detecting unexpected messages, such as sending the fingerprint for the same range over and over again.
An intuitive choice for range representation within the ordered set
would be [a,b] (from a to b inclusive). But say we want to divide
on a middle point m. Then we will have [a,m-1] and [m,b], so we
will also need item decrement operation to be defined the items in the
set. Another problem is, how to represent a range that covers the
whole set? We'd have to use MIN and MAX to be able to use
[MIN,MAX] as such a range representation.
Actually, with set keys being defined as fixed length byte sequences, these difficulties are not overly important; yet for now, the reconciler uses the range notation from the original "Range-Based Set Reconciliation" paper.
The notation we use is [a,b), that is the a bound is inclusive and
the b is non-inclusive.
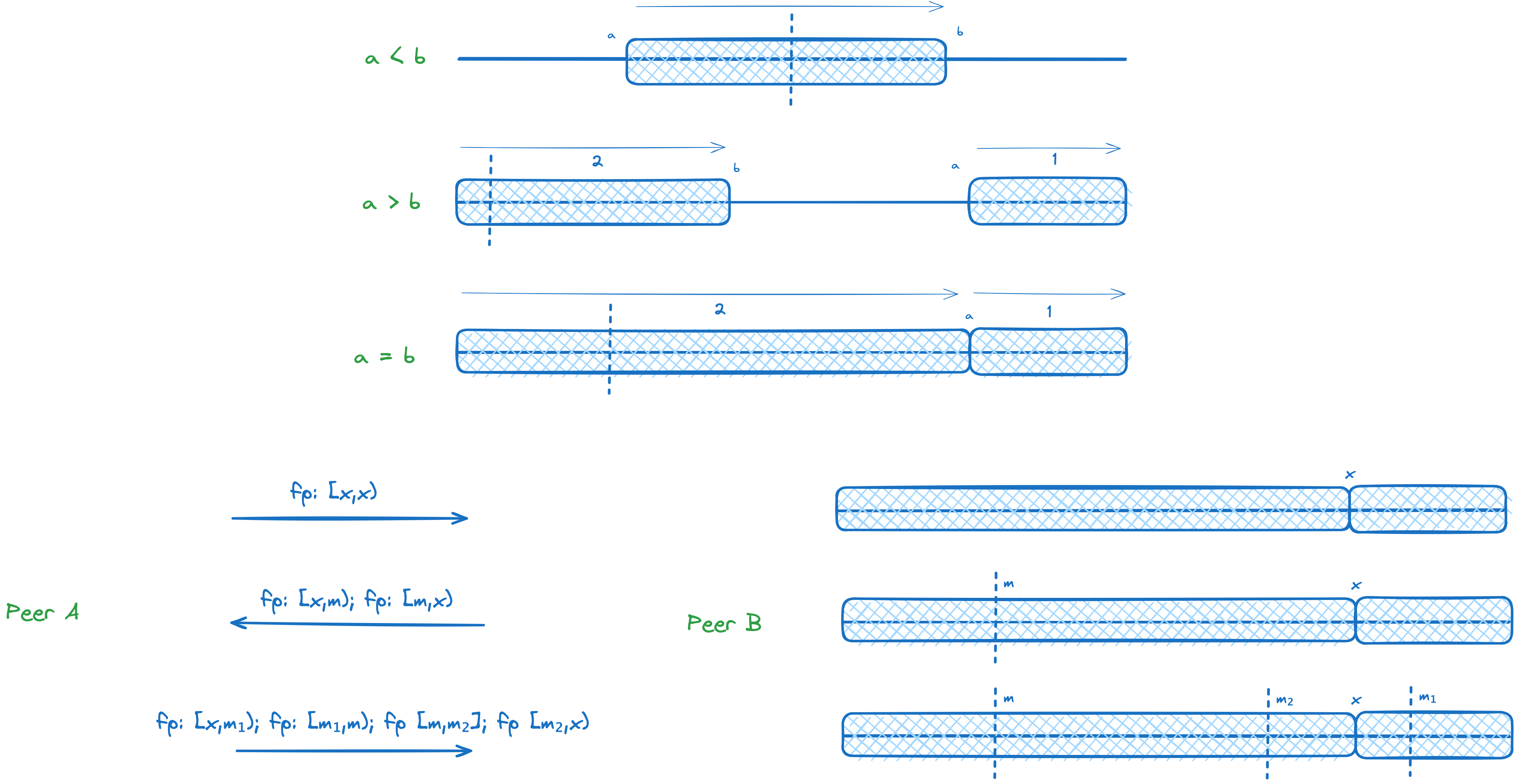
There's a catch, though: wraparound ranges. There are following kinds of ranges:
- if
a < b: "normal" range - if
a > b: "wraparound" ("inverse") range[a,b)represents[MIN,a) ∪ [b,MAX] [a,a)represents the whole range (that's actually just a special case of the wraparound range)
The following diagram shows different types of ranges, and also
illustrates how the ranges can be subdivided into smaller ones, with
dashed lines marking "middle" subdivision points which are used by
the set reconciler to split the ranges recursively.
Note that subdivisions of the ranges are done based on the N of
elements, so not necessarily close to (a+b)/2.
The recursive reconciliation algorithm, when used with randomly distributed element values (such as hash IDs), is only efficient for relatively small difference between the sets, probably around a few %. Above that, sending the whole range contents is often a better strategy. The resulting extra load on the network can be distributed between multiple peers by asking the different peers for the contents of different subranges.
Thus, we need a method to gauge the difference between the local set and the remote one. Using mere item count for this may often be imprecise, as there can be situations where sets may have similar counts yet different elements.
Currently, MinHash probing is used to approximate Jaccard similarity coefficient (Jaccard index) between sets belonging to different peers:
J(A, B) = |A∩B| / |A∪B|
The approximation is done by picking a sample, that is a fixed number of lowest-valued items (keys) from the set and comparing it to a sample with the same number of items from the remote peer.
Unlike most MinHash implementations, we don't need to do the actual hashing b/c the items in the set (keys) are already hash values.
During periods when a lot of new items arrive in quick succession (e.g. ATX IDs during the cycle gaps), the sets differences between peers may become too large for efficient recursive sync quickly.
As the sync algorithm is still good for fixing small differences between the sets, we can improve the situation by "priming" the sync, which means sending all the items received during last N seconds/minutes before beginning the actual sync. This may mean some excess items may be sent which are present on both peers, but it also means that the difference between the sets will be reduced, hopefully avoiding the "send all items" fallback.
See Recent message for the details.
The set reconciliation protocol uses a number of different messages that can be grouped as related to the set reconciliation, MinHash probing, and recent sync.
Some of the messages listed below are markers which do not carry any extra information besides the message type.
Different messages have different expectations of possible responses associated with them:
- no response
- a possible response (0..n messages sent back)
- a required response (1..n messages sent back)
All the messages between synchronizing peers are sent in rounds, each
round except the last one being concluded with EndRound marker, and
the last round being concluded with Done marker.
In the diagrams provided in the sections following "Round messages",
the round messages EndRound and Done are omitted for the sake of
simplicity.
This message is sent at the end of reconciliation process by the peer
that has determined that it's in sync with another party. The sync
process terminates with one peer sending Done message and another
one receiving it. This message is a marker, that is, it doesn't carry
any extra information.
The condition for the Done message being sent is:
- after processing all of the messages from the last round, no messages were generated that expect any response.
No response is expected to the Done message.
sequenceDiagram
A->>B: Done
This message is sent at the end of the reconciliation round, when all
the messages up to and including the EndRound message have been
processed and responses sent back. This message is a marker, that is,
it doesn't carry any extra information.
The EndRound message is NOT sent after processing all of the peer's
round messages in the following case:
- after processing all of the messages from the last round, no
messages were generated that expect any response.
In this case,
Donemessage is sent instead.
sequenceDiagram
A->>B: EndRound
Set reconciliation messages deal with making sure two sets belonging
to different peers A and B are equal.
This message is sent by a party which doesn't have any items in the set and no way to pick a bounding value (no bounds were provided to the reconciler). This message is a marker, that is, it doesn't carry any extra information.
If the remote peer's set is also empty, the remote peer responds with
EmptySet message.
sequenceDiagram
Note over A: The set is empty
A->>B: EmptySet
Note over B: The set is empty
B->>A: EmptySet
If the remote peer's set is not empty, the remote peer sends back its
whole set via a number of ItemChunk messages.
sequenceDiagram
Note over A: The set is empty
A->>B: EmptySet
Note over B: The set is <br/> not empty
loop
B->>A: ItemChunk <br/> (Items)
end
EmptyRange message is similar to the EmptySet message except that
it applies to a subrange instead of the whole set.
Parameters:
X: start of the rangeY: end of the range
If the remote peer's [X,Y) range is also empty, the remote peer
responds with EmptySet message.
sequenceDiagram
A->>B: EmptyRange <br/> (X, Y)
B->>A: EmptyRange <br/> (X, Y)
If the remote peer's [X,Y) range is not empty, the remote peer
sends back all the items in the range via a number of ItemChunk
messages.
sequenceDiagram
A->>B: EmptyRange <br/> (X, Y)
loop
B->>A: ItemChunk <br/> (Items)
end
Fingerprint message carries the fingerprint and count values for a
specific range. If two ranges with the same [X,Y) bounds have the
same fingerprint for both peers, the corresponding bounded subsets are
considered to be equal (in sync).
Parameters:
X: start of the rangeY: end of the rangeCount: number of items in the rangeFingerprint: the fingerprint of the range
Upon receiving a Fingerprint message for a range for which the local
fingerprint equals to the message's fingerprint value, no response is
generated.
sequenceDiagram
A->>B: Fingerprint <br/> (X, Y, Count, Fingerprint)
Note over B: Fingerprint matches, <br/> no response
If the fingerprint doesn't match and the range is small enough
(<=maxSendRange), the contents of the range is sent back via a
number of ItemChunk messages, followed by a RangeContents message
which will instruct the peer to send back any items it has in the
[X,Y) range.
sequenceDiagram
A->>B: Fingerprint <br/> (X, Y, Count, Fingerprint)
Note over B: Fingerprint doesn't match, <br/> the range is small enough
loop
B->>A: ItemChunk
end
B->>A: RangeContents <br/> (X, Y, Count)
If the fingerprint doesn't match and the range is big enough
(>maxSendRange), the range is split in two using some middle point
m, and Fingerprint messages are sent back for the each part.
sequenceDiagram
A->>B: Fingerprint <br/> (X, Y, Count, Fingerprint)
Note over B: Fingerprint doesn't match, <br/> the range is big enough
Note over B: Split the range in two <br/> using middle point m
B->>A: Fingerprint <br/> (X, m, Count, Fingerprint)
B->>A: Fingerprint <br/> (m, Y, Count, Fingerprint)
RangeContents message notifies the peer that the contents of the
specific range was sent via ItemChunk messages, and requests back
the contents of the range.
Parameters:
X: start of the rangeY: end of the rangeCount: number of items in the range
If the local range is empty, no response is generated to RangeContents.
sequenceDiagram
loop
A->>B: ItemChunk
end
A->>B: RangeContents <br/> (X, Y, Count)
If the local range is not empty, the items in the range are sent back
via a number of ItemChunk messages.
sequenceDiagram
loop
A->>B: ItemChunk
end
A->>B: RangeContents <br/> (X, Y, Count)
loop
B->>A: ItemChunk
end
ItemBatch message contains a number of actual set items (keys).
If the items in the range being sent do not fit into a single
ItemBatch message, multiple ItemBatch messages are used.
No response is expected.
Parameters:
Items: set items (keys)
sequenceDiagram
loop
A->>B: ItemChunk
end
When beginning pairwise set reconciliation, if WithMaxDiff option is
used with positive Jaccard distance (1-J(A,B)) value, a Sample
message is sent so that the peer can decide whether it's set is
similar enough to the other set for efficient recursive reconciliation,
or if "send all items" fallback needs to be used.
Besides that, there's separate probing sequence which is used to
determine the difference between the sets without doing the actual
reconciliation. In this case, a Probe message is sent, to which a
Sample message is sent by another peer as the response.
Probing is used by the multipeer reconciler to decide on the sync
strategy to use.
Probe message requests a sample of lowest-values items (keys) for
Jaccard index approximation.
Parameters:
X: start of the rangeY: end of the rangeFingerprint: the fingerprint of the rangeSampleSize: the number of items in the sample
Sample message is always generated as the response to Probe
message.
sequenceDiagram
A->>B: Probe <br> (X, Y, Fingerprint, SampleSize)
B->>A: Sample <br> (X, Y, Count, Fingerprint, Items)
Sample message carries a sample of lowest-valued items (keys) from
the set for Jaccard index approximation. Only a fixed number of lowest
bits from each item is used, b/c collisions are not critical in this
context and may only cause slightly less precise approximation.
Parameters:
X: start of the rangeY: end of the rangeFingerprint: the fingerprint of the rangeItems: the actual sample items
During probing, when Sample is generated as a response to Probe
message, no response is generated.
sequenceDiagram
A->>B: Sample <br> (X, Y, Count, Fingerprint, Items)
When Sample message is used during sync, the peer receiving the
Sample message either sends back all its items in the range if
Jaccard distance exceeds maxDiff, along with RangeContents message
to request the range contents, or proceeds with normal sync initiation
sequence without further MinHash or recent message processing. There
can also be a shortcut when the fingerprint value in the Sample
message matches that of the same range in the local set, in which
case no responses are generated to the Sample message.
The difference is too big:
sequenceDiagram
A->>B: Sample <br/> (X, Y, Count, Fingerprint, Items)
Note over B: MinHash diff <br/> is too large
loop
B->>A: ItemChunk <br/> (Items)
end
B->>A: RangeContents <br/> (X, Y, Count)
The difference is acceptable:
sequenceDiagram
A->>B: Sample <br/> (X, Y, Count, Fingerprint, Items)
Note over B: MinHash diff <br/> is acceptable
Note over B: Fingerprint is different from local one
B->>A: Fingerprint <br/> (X, Y, Count, Fingerprint)
Note over A: Range fingerprint differs <br/> Choose middle point m
A->>B: Fingerprint <br/> (X, m, Count1, Fingerprint1)
A->>B: Fingerprint <br/> (m, Y, Count2, Fingerprint2)
No difference according to the fingerprint:
sequenceDiagram
A->>B: Sample <br/> (X, Y, Count, Fingerprint, Items)
Note over B: Fingerprint matches
This message is used for Recent sync. It is sent as the initial message when recent sync is enabled.
Recent message is preceded by a number of ItemChunk messages
carrying the actual items (keys). The items in immediately preceding
ItemChunk message must be added to the set immediately before
proceeding with further reconciliation.
Parameters:
SinceTime: nanoseconds since Unix epoch marking the beginning of recent items that were sent, according to the local timestamp. IfSinceTimeis zero, this indicates a response to another Recent message.
As a response to Recent message, the local items starting from
SinceTime according to their local timestamp are sent to the peer
via a number of ItemChunk messages, followed by Recent message
with zero timestamp, indicating that the items need to be added to the
set immediately before proceeding with further reconciliation. After
that the sync sequence without further Recent message but with or
without MinHash probing is initiated, depending on whether a positive
maxDiff value is set via the WithMaxDiff option.
sequenceDiagram
Note over A: Send recently <br/> received items
loop
A->>B: ItemChunk <br/> (Items)
end
A->>B: Recent <br/> (Since)
Note over B: Send recently <br/> received items
loop
B->>A: ItemChunk <br/> (Items)
end
B->>A: Recent <br/> (Since=0)
Note over B: The sample is taken <br/> after consuming <br/> the recent items from A
B->>A: Sample <br/> (X, Y, Count, Fingerprint, Items)
The sync initiation sequences outlined below depend on the set contents as well as on the set reconciliation options, in particular:
WithMaxSendRange: max range size to send w/o any further recursive reconciliationWithMaxDiff: max Jaccard distance (1-J(A,B),J(A,B)being the approximation of Jaccard index) to be considered for further recursive reconciliation. The MinHash check is only performed when this option is set to a positive value.WithRecentTimeSpan: max time span for sending recent items. Setting this enables sendingRecentmessages.
Sync between two empty sets or empty ranges. An EmptySet message is
used when the set is empty and thus bounding values cannot be chosen
from it.
sequenceDiagram
A->>B: EmptySet
A->>B: EndRound
B->>A: EmptySet
B->>A: Done
sequenceDiagram
A->>B: EmptyRange <br/> (X, Y)
A->>B: EndRound
B->>A: EmptyRange <br/> (X, Y)
B->>A: Done
Sync between an empty set (A) and a non-empty one (B).
sequenceDiagram
A->>B: EmptySet
A->>B: EndRound
loop
B->>A: ItemChunk <br/> (Items)
end
B->>A: Done
Sync between small ranges (size <= maxSendRange):
sequenceDiagram
loop
A->>B: ItemChunk <br/> (Items)
end
A->>B: RangeContents <br/> (X, Y, Count)
A->>B: EndRound
loop
B->>A: ItemChunk <br/> (Items)
end
B->>A: Done
Sync between two equal sets:
sequenceDiagram
A->>B: Fingerprint <br/> (X, Y, Count, Fingerprint)
A->>B: EndRound
Note over B: Fingerprint matches
B->>A: Done
Sync between two different large enough sets:
sequenceDiagram
A->>B: Fingerprint <br/> (X, Y, Count, Fingerprint)
A->>B: EndRound
Note over B: Range fingerprint differs <br/> Choose middle point m
B->>A: Fingerprint <br/> (X, m, Count1, Fingerprint1)
B->>A: Fingerprint <br/> (m, Y, Count2, Fingerprint2)
B->>A: EndRound
Note over A, B: ... more interactions ...
A->>B: Done
Sync with failed MinHash check (sets too different). This causes the reconciler to fall back to sending the contents of the whole range.
sequenceDiagram
A->>B: Sample <br/> (X, Y, Count, Fingerprint, Items)
A->>B: EndRound
Note over B: MinHash diff <br/> is too large
loop
B->>A: ItemChunk <br/> (Items)
end
B->>A: RangeContents <br/> (X, Y, Count)
B->>A: Done
Sync with successful MinHash check (acceptable difference). Normal set reconciliation follows.
sequenceDiagram
A->>B: Sample <br/> (X, Y, Count, Fingerprint, Items)
A->>B: EndRound
Note over B: MinHash diff <br/> is acceptable
Note over B: Fingerprint is different from local one
B->>A: Fingerprint <br/> (X, Y, Count, Fingerprint)
B->>A: EndRound
Note over A: Range fingerprint differs <br/> Choose middle point m
A->>B: Fingerprint <br/> (X, m, Count1, Fingerprint1)
A->>B: Fingerprint <br/> (m, Y, Count2, Fingerprint2)
A->>B: EndRound
Note over A, B: ... more interactions ...
B->>A: Done
Sync with requested MinHash check and matching fingerprint and count (equal sets). No further set reconciliation is necessary.
sequenceDiagram
A->>B: Sample <br/> (X, Y, Count, Fingerprint, Items)
A->>B: EndRound
Note over B: Fingerprint matches
B->>A: Done
Recent sync with MinHash check. After receiving the message of type Recent, side B acts as if it was the initiating side in the previous case.
sequenceDiagram
Note over A: Send recently <br/> received items
loop
A->>B: ItemChunk <br/> (Items)
end
A->>B: Recent <br/> (Since)
A->>B: EndRound
Note over B: Send recently <br/> received items
loop
B->>A: ItemChunk <br/> (Items)
end
Note over B: The sample is taken <br/> after consuming <br/> the recent items from A
B->>A: Sample <br/> (X, Y, Count, Fingerprint, Items)
B->>A: EndRound
Note over A: MinHash diff <br/> after consuming <br/> the recent items from B <br/> is acceptable
A->>B: Fingerprint <br/> (X, Y, Count, Fingerprint)
A->>B: EndRound
Note over B: Range fingerprint differs <br/> Choose middle point m
B->>A: Fingerprint <br/> (X, m, Count1, Fingerprint1)
B->>A: Fingerprint <br/> (m, Y, Count2, Fingerprint2)
B->>A: EndRound
Note over A, B: ... more interactions ...
A->>B: Done
Probe sequence. This is used to check how peers are different from this one by the multipeer reconciliation algorithm, and does not involve the actual sync.
sequenceDiagram
A->>B: Probe <br> (X, Y, Fingerprint, SampleSize)
A->>B: EndRound
B->>A: Sample <br> (X, Y, Count, Fingerprint, Items)
B->>A: Done
The following are some improvements to be considered for the set reconciler. They may need a bit more thinking before being converted to issues.
Another issue is ItemChunk messages. It would be much better to
receive the items (keys) in a streamed manner and just propagate them
to the respective handlers immediately.
Right now, the set reconciliation protocol uses 12-byte fingerprints
all the time. It should be possible, though, to use smaller
fingerprints, e.g. 4-byte (32-bit), and mitigate the possible
collisions by using checksums. One approach could be: when a range for
which fingerprint has been received turns out to be synced, its
fingerprint is XORed together with other such synced ranges from the
same round, and the resulting checksum is sent back as full 12 bytes
at the end of a new round as a part of EndRound or Done message.
The other peers checks which range fingerprints went unanswered (b/c
they're already synchronized), calculates the full fingerprint on its
side and compares it with the one received in EndRound / Done
message. If there's a mismatch, the synced range fingerprints are sent
again, this time with full fingerprints.
An important part of fingerprints is the need to use the lower bits of
each ID and not the higher bits which tend to be the same across
smaller ranges at higher recursive subdivision depths.
The initial Recent message could carry a Bloom filter for recently
received items instead of all the items themselves. The peer could
then send back the items for which the filter check is negative,
followed by the initial peer sending the items it has for the same
time span that weren't received yet. While Bloom filters may have
false positives, this is not critical for the sync priming mechanism
as we don't need the sets to be exactly same after the recent sync; we
just want to bring them closer to each other. That being said, a
sufficient size of the Bloom filter needs to be chosen to minimize the
number of missed elements.
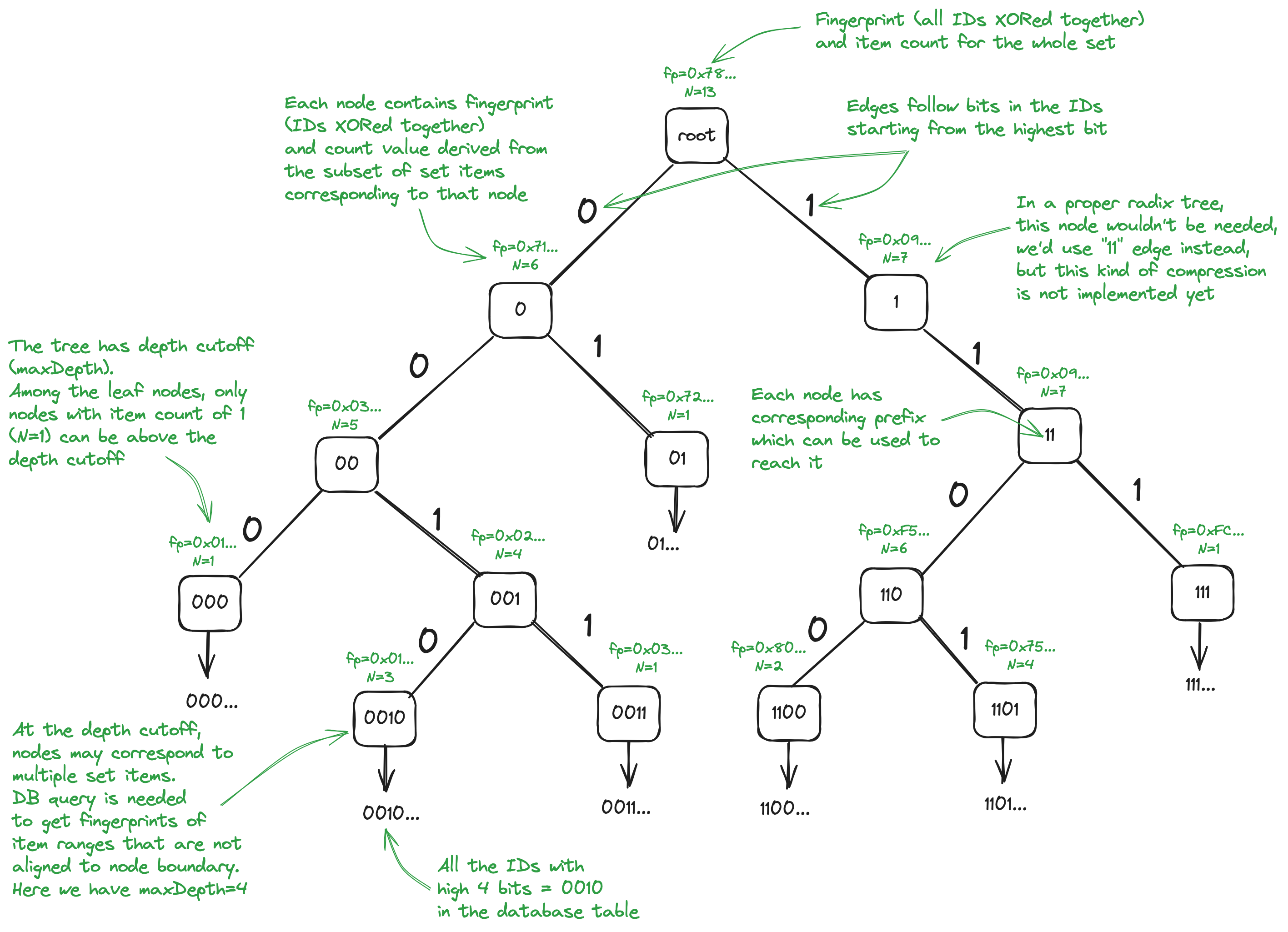
FPTree (fingerprint tree) is data structure intended to facilitate synchronization of objects stored in an SQLite database, with hash-based IDs. It stores fingerprints (IDs XORed together) and item counts for ID ranges.
FPTree has the following properties:
- FPTree is an in-memory structure that provides efficient item count and fingerprints for ID (item/key) ranges, trying to do its best to avoid doing database queries. The queries may be entirely avoided if ranges are aligned on the node boundaries.
- FPTree is a binary trie (prefix tree), following the bits in the IDs starting from the highest one. The intent is to convert it to a proper radix tree instead, but that's not implemented yet.
- FPTree relies on IDs being hashes and thus being uniformly distributed to ensure balancedness of the tree, instead of using a balancing mechanism such as red-black tree.
- FPTree provides a range split mechanism (needed for pairwise sync) which tries to ensure that the ranges are aligned on node boundaries up to certain subdivision depth.
- Full FPTree copy operation is
O(1)in terms of time and memory. The copies are safe for concurrent use. - FPTree can also store the actual IDs without the use of an underlying table.
- FPTrees can be "stacked" together. The FPTree-based
OrderedSetimplementation uses 2 FPTrees, one database-bound and another one fully in-memory. The in-memory FPTree is used to store fresh items received via the Recent sync mechanism. - FPTrees performs queries on ranges
[x,y), supporting normalx < yranges, as well as wraparoundx > yranges and full set range[x,x)(see Range representation). - Each FPTree node has corresponding bit prefix by which it can be reached.
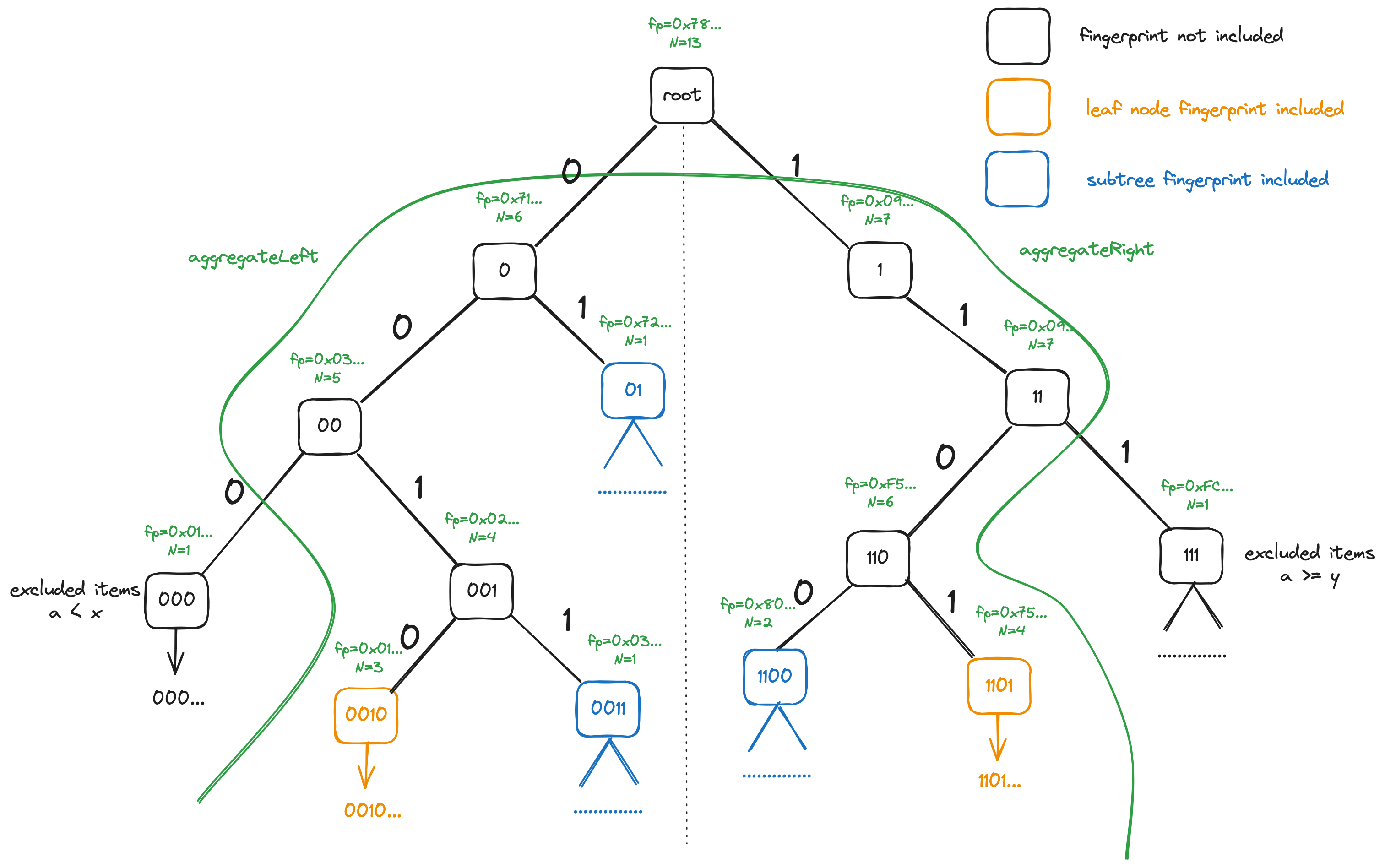
The tree structure is shown on the diagram below. The leaf nodes correspond to the rows in database table with IDs having the bit prefix corresponding to the leaf node.
As it is mentioned above, FPTree itself can also store the actual IDs, without using an underlying database table.\
Aggregation means calculation of fingerprint and item count for a
range. The aggregation is done using different methods depending on
whether the [x,y) range is normal (x<y), wrapped around (x>y) or
indicates the whole set (x=y). Aggregation may also be bounded by
the maximum number of items to include. The easiest case is full set
aggregation, in which we just take the fingerprint and count values
from the root node of the FPTree.
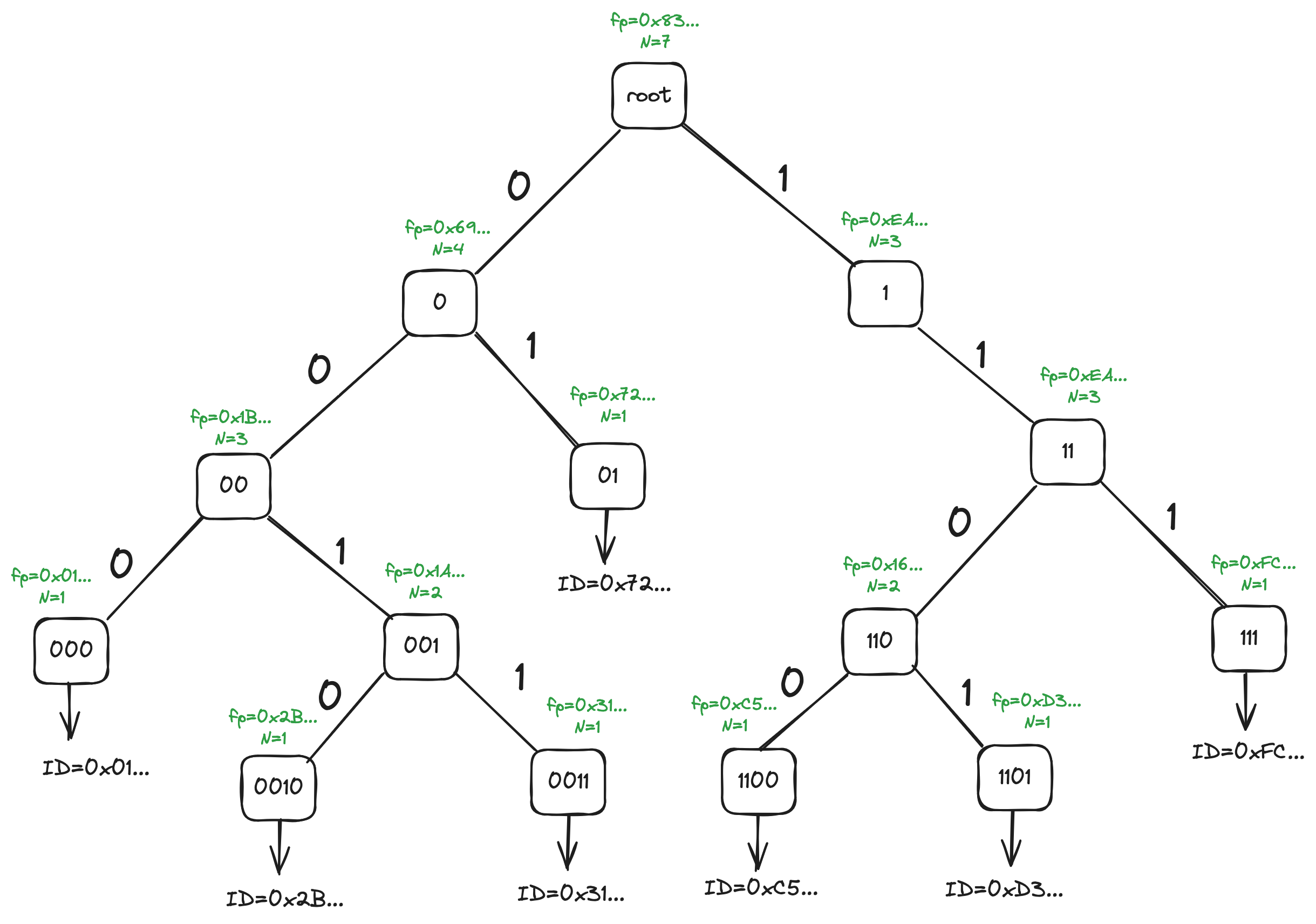
In case of a normal range [x,y) with x<y is done starting from the
lowest common ancestor (LCA) of the nodes corresponding to x and
y, as all the nodes that are not descendants of that LCA do not fall
into the [x,y) range. Let's say we need to find the fingerprint and
item count for a range with x=0x20... (highest byte only shown) and
y=0xD9.... As x starts with bit 0 (highest bit), and y starts
with 1, they have no common prefix and thus the LCA node is the root
node.
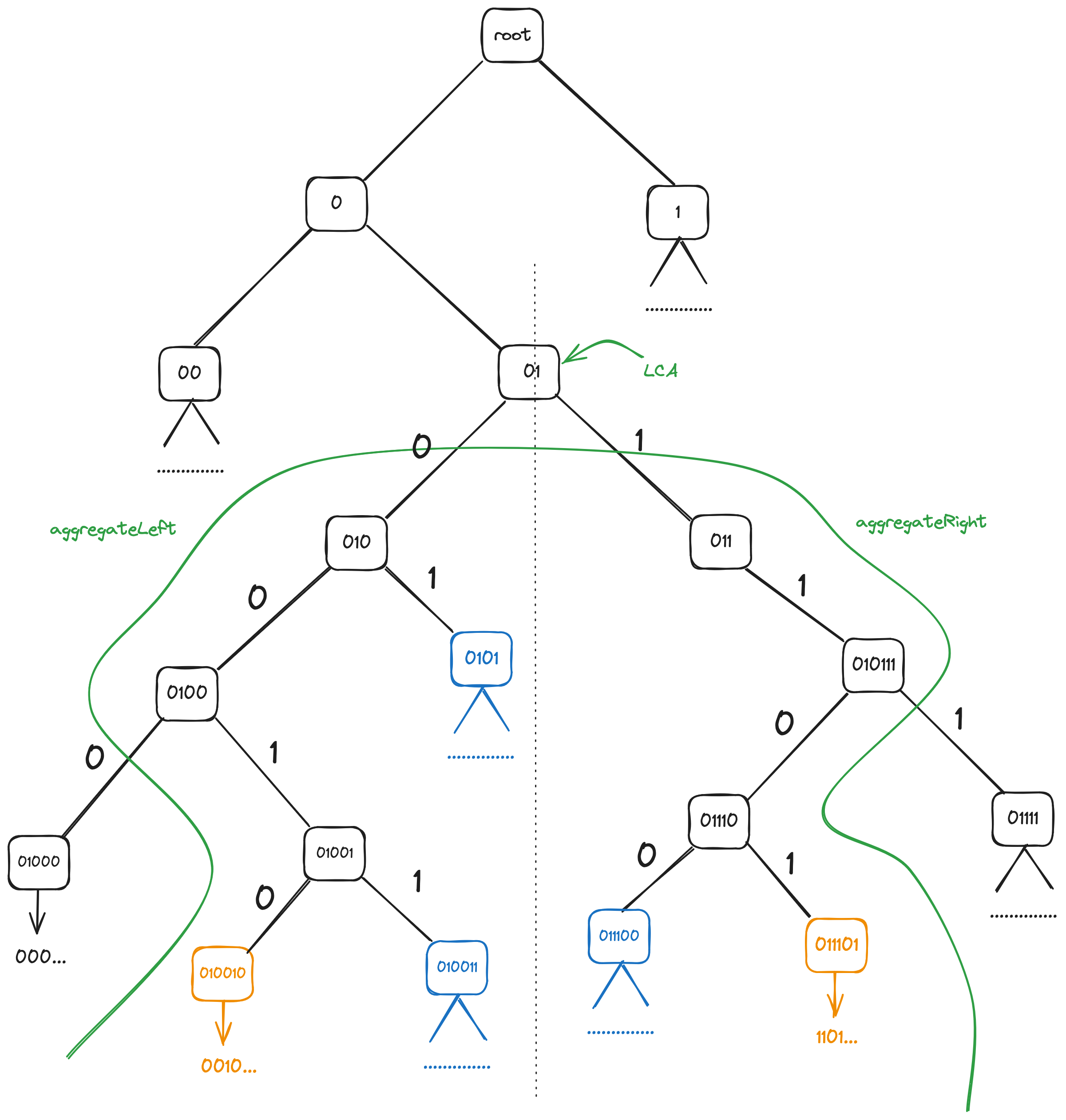
Aggregation is done in two parts: left-side aggregation
(aggregateLeft), which is done on all nodes in the left subtree of
the LCA, and right-side aggregation (aggregateRight) which is done
on the right subtree of the LCA.
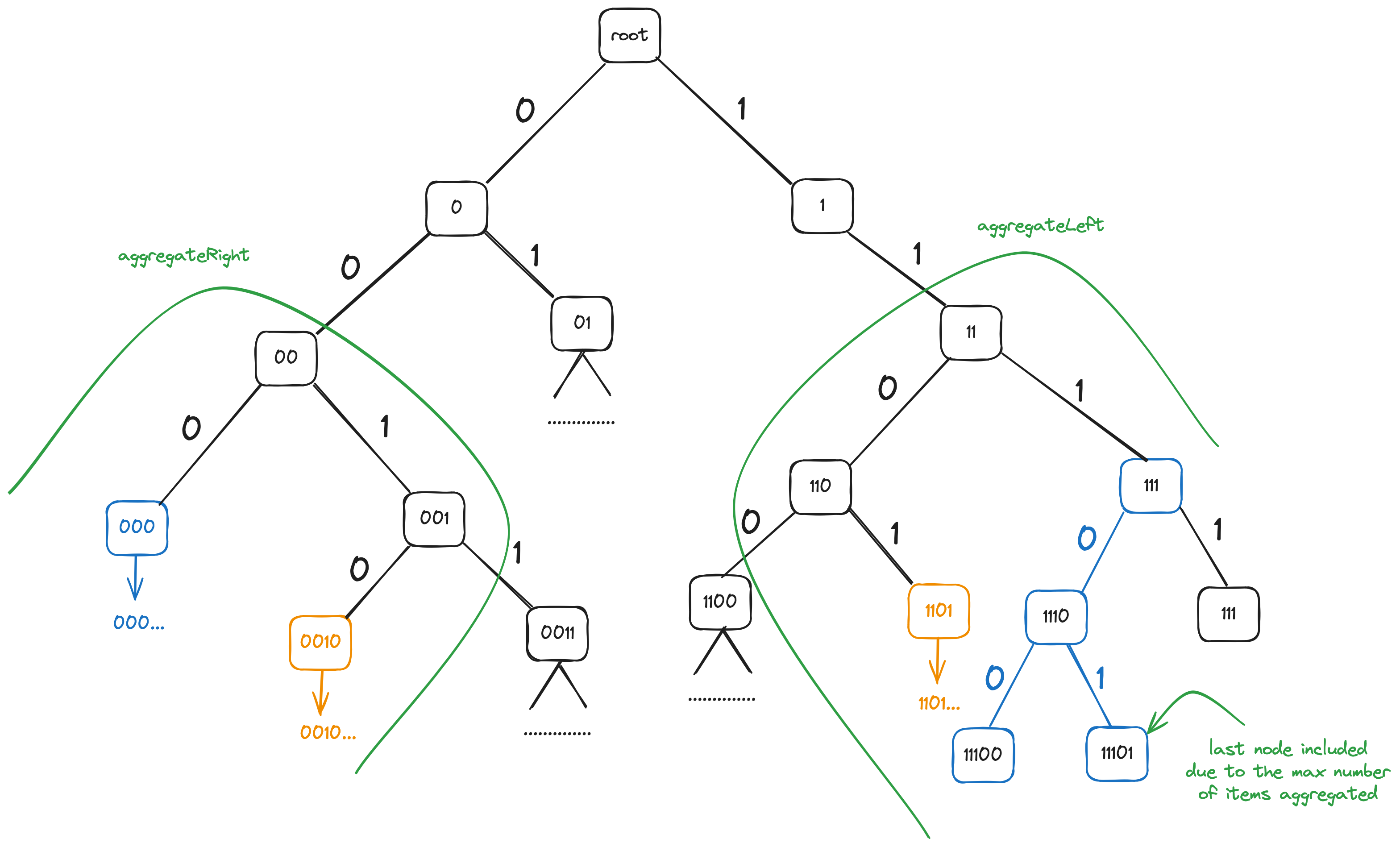
Left aggregation (aggregateLeft) is done like this: we follow the
bits of the ID (note that in the picture below, where left aggregation
starts with node 0, this doesn't include the highest bit which was
"used up" already b/c we're starting with the left subtree).
If we encounter 0, we include the right child's count and fingerprint
in aggregation (01, 0011 nodes shown in blue), and then we descend
to the left node.
If we encounter 1, we just descend to the right node.
Upon reaching a leaf node, in case if the tree is database-bound, we
use SELECT to get items from the table which fall within the [x,y)
range and correspond to that leaf node (having corresponding bit
prefix), and include these nodes' fingerprints and counts in
aggregation.
Right aggregation (aggregateRight) is inverse of left
aggregation. We also follow the bits of the ID, but upon a 0, we
just descend to the left child, and upon 1, we include the left
subtree of the current node and descend to the right. The leaf nodes
are handled similarly to the left aggregation.
Another figure below shows aggregation starting from a non-root LCA,
with x=0x48... and y=0xD6....
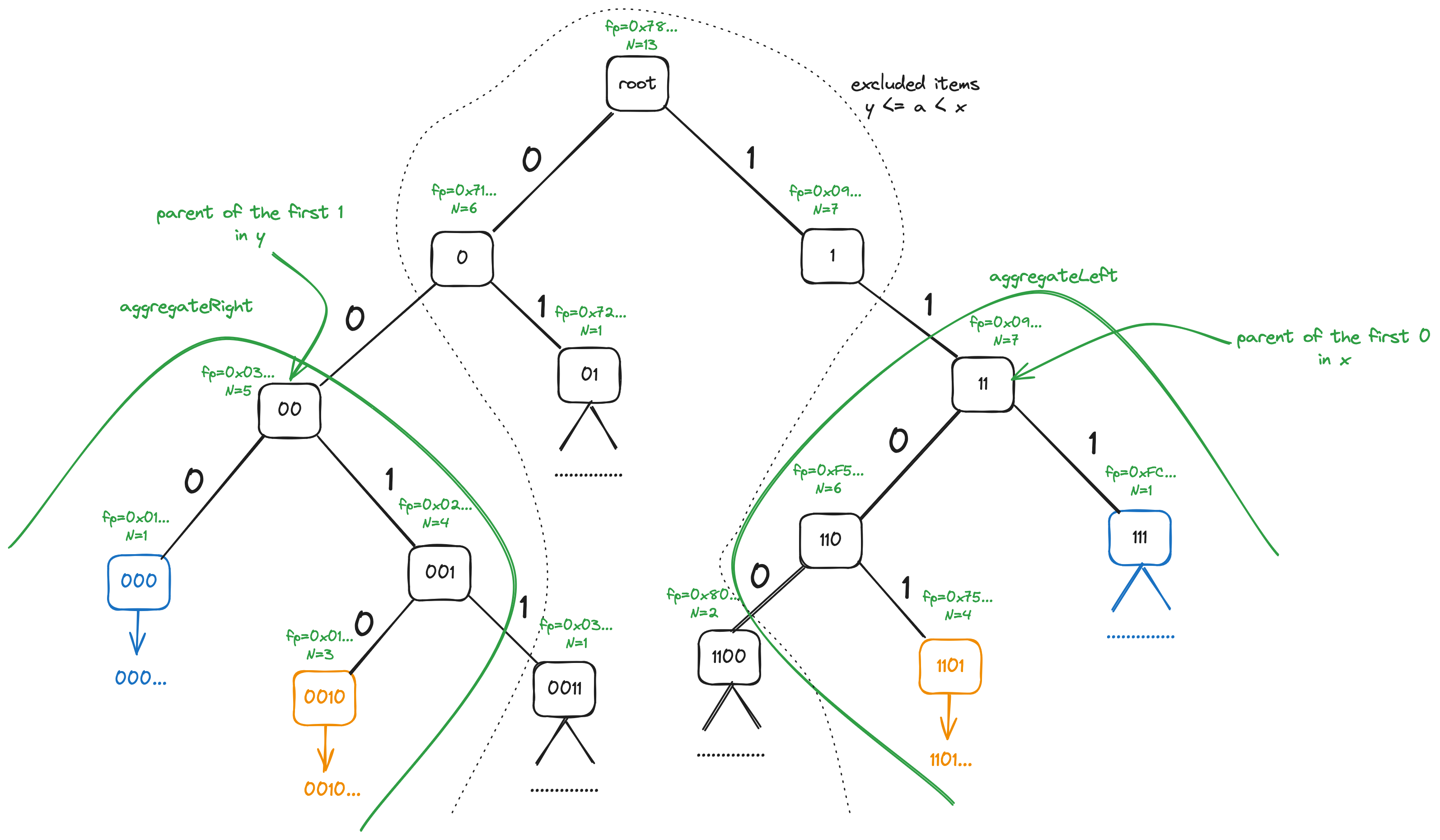
In case of wraparound ranges [x,y) with x>y, aggregateLeft and
aggregateRight are used, too. Somewhat unintuitively, in this case
aggregateLeft is used on the right side of the tree, b/c that's
where the beginning ("left side") of the wrapped-around [x,y) range
lies, whereas aggregateRight is applied to the left side of the tree
corresponding to the end ("right side") of the range.
The subtree on which aggregateLeft is done is rooted at the node
reachable by following the longest prefix of x consisting entirely
of 1s. Conversely, the subtree on which aggregateRight is done is
rooted at the node reachable by following the longest prefix of y
consisting entirely of 0s.
The figure below shows aggregation of the [x,y) range with
x=0xD1.. and y=0x29.
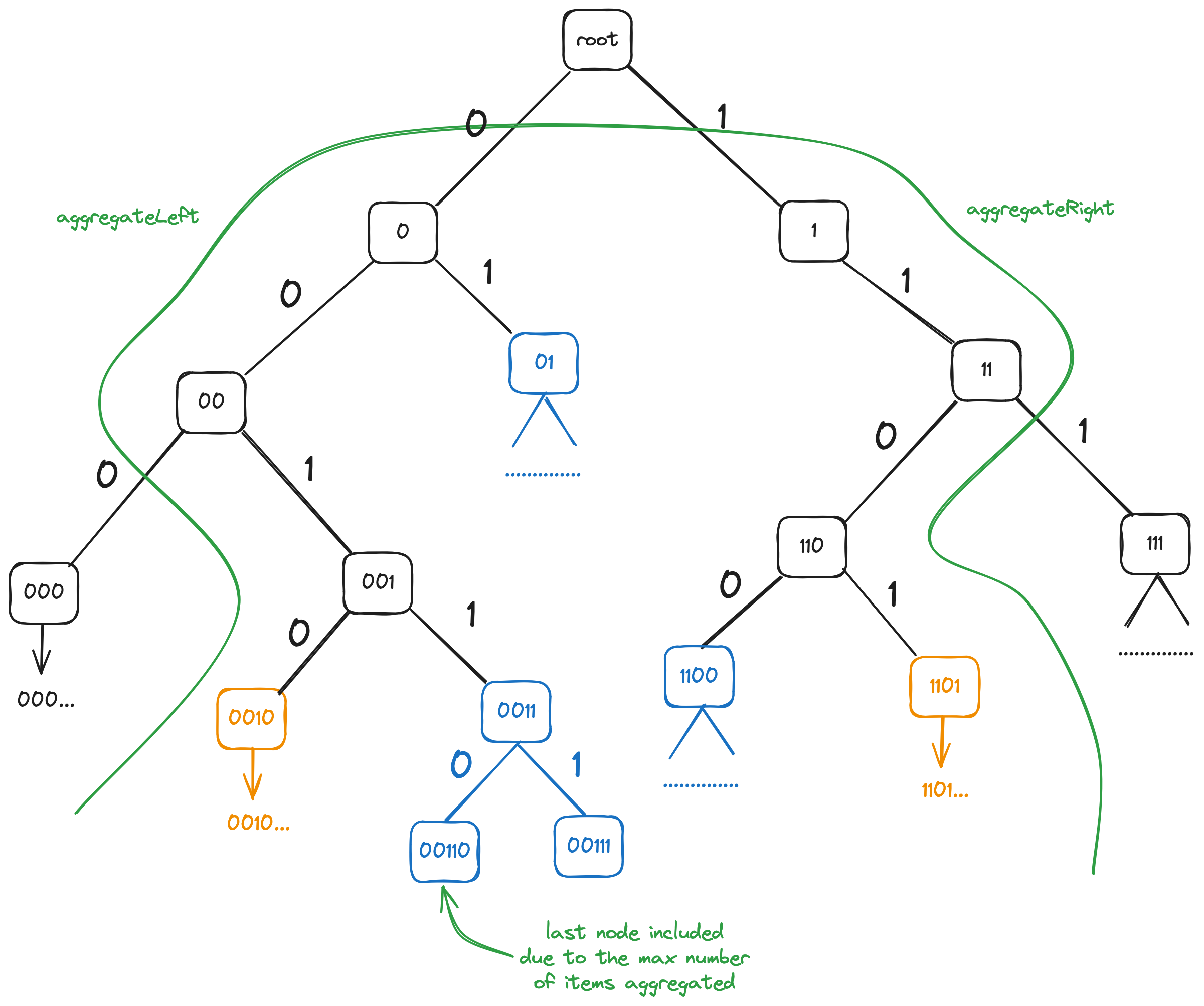
During recursive set reconciliation, range split operation often needs to be performed. This involves partitioning the range roughly in half with respect to the number of items in each new subrange, and calculating item count and fingerprint for each part resulting from the split. FPTree will try to perform such an operation on node boundary, but if the range is to small or not aligned to the node boundary, the following is done:
- The number of items in the range obtained (
N). - The items in the range are aggregated with the cap on maximum
aggregated count equal to
N/2, and the non-inclusive upper bound of the aggregated subrange is noted (m). The aggregated items can be said to lie in range[x,m) - The second half of the range is aggregated starting with
m. This part of the range is[m,y).
In both cases, the operation is based upon imposing the limit on number of items aggregated. In the easy, node-aligned case, the aggregation continues after exhausting the limit on the total item count, but using separate places for accumulation of remaining nodes' fingerprints and counts. The initial accumulated fingerprint and count are returned for the first resulting subrange, and the second accumulated fingerprint and count are returned for the second subrange resulting from the partition. In case if node-aligned "easy split" cannot be done, aggregation stops after exhausting the limit.
When limited aggregation is done, instead of including full right
subtrees during aggregateLeft, including full left subtrees during
aggregateRight, and including the whole tree during [x,x) (full
set) range aggregation, when subtree count exceeds the remaining limit
after processing all the nodes visited so far, the corresponding
subtrees are descended into to find the cutoff point.
Below limited aggregation is shown for a normal x<y range:
In similar way, the cutoff point is located when aggregating wrapped around ranges:
FPTree nodes are stored in a reference-counted pool. The rationale for using the pool is the following:
- GC pressure and heap fragmentation are reduced
- instead of 64-bit pointers, 32-bit indices are used to refer to the nodes in the pool, which is enough given expected number of IDs stored in the tree
Each FPTree node is represented by a structure contains the following info:
- left and right nodes (if present), corresponding to the following
0or1bit, referred - item count in the ID subset with the corresponding prefix
- item fingerprint in the ID subset with the corresponding prefix
- reference count
Reference count includes the number of other nodes (belonging to different copies of the tree which may differ) referring to this node plus the number of FPTrees that have the particular node as their root.
Tree copy operation increments its root's count by 1.
When a new item is added to the FPTree, as many nodes as possible of the original tree are reused. The old nodes which are no longer used by the tree after the release operation have their reference counts decremented as necessary. Nodes that reach reference count of 0 are released back to the pool and reused for new nodes.
Additionally, there's a hash table linking pool indices to actual ID values in case if the FPTree stores values (that is, the FPTree is not database-bound). The hash table entries are removed when pool entries are released.
FPTree also uses finalizer to make sure pool nodes are released when the tree object is being GC'd by the Go runtime.
Node pool uses read-write locking with multiple reader locks but a single write lock allowed at any time to ensure thread safety.
When accessing database, the IDs in the underlying table, e.g. atxs,
must correspond to the state of the FPTree object. Yet, the tree may not
be synchronized immediately with the table when new IDs are added.
Moreover, the copies of the original set include database-bound FPTree
that must not change even when new IDs are added to the database table.
To solve this issue, the code relies on the ever-increasing SQLite
rowid values in the append-only tables such as atxs. Eventually,
explicit integer autoincrement ID column will be used, which always
ensures that old rowids (equal to these integer IDs in that case) are
not reused, but for most practical purposes it's safe to assume rowids
aren't reused change while go-spacemesh runs.
When an OrderedSet (the database-bound implementation is called
DBSet) is first built from the database table, the max rowid value
for the table is remembered and then used in a filter in database
queries. Afterwards, as new IDs arrive, DBSet can be "advanced" by
increasing max rowid value used in the filter and updating FPTree to
include new IDs. The state of the table defined by maximum rowid value
is called "snapshot".
The implementation of database-bound FPTrees has several layers.
sync2/sqlstorepackage implements relatively simple sequence implementations that can be used to iterate over database tables, based on ID ranges and also local timestamps in case of recent syncsync2/fptreecontains FPTree implementation itself, which can usesync2/sqlstoreas underlying ID storagesync2/dbsetis anOrderedSetimplementation based onFPTree
Below are SQL queries used for a database-bound FPTree in
sync2/sqlstore. The queries are auto-generated from table
description. The table description may include additional filter, in
this case ATX epoch ID.
Select maximum current rowid for a table:
SELECT max("rowid") FROM "atxs"Select number of IDs in the snapshot (used to pre-allocate the FPTree node pool):
SELECT count("id") FROM "atxs" WHERE "epoch" = ? AND "rowid" <= ?Select the IDs in the snapshot:
SELECT "id" FROM "atxs" WHERE "epoch" = ? AND "rowid" <= ?Select IDs starting from the specified ID, this is used in database sequences which are in turn used to get IDs for an FPTree leaf:
SELECT "id" FROM "atxs" WHERE "epoch" = ? AND "id" >= ? AND
"rowid" <= ? ORDER BY "id" LIMIT ?Select number of recently received items items for recent sync (which is not done using FPTree):
SELECT count("id") FROM "atxs" WHERE "epoch" = ? AND
"rowid" <= ? AND "received" >= ?Select recently received IDs:
SELECT "id" FROM "atxs" WHERE "epoch" = ? AND "id" >= ? AND
"rowid" <= ? AND "received" >= ? ORDER BY "id" LIMIT ?The multi-peer reconciliation approach is loosely based on SREP: Out-Of-Band Sync of Transaction Pools for Large-Scale Blockchains paper by Novak Boškov, Sevval Simsek, Ari Trachtenberg, and David Starobinski.
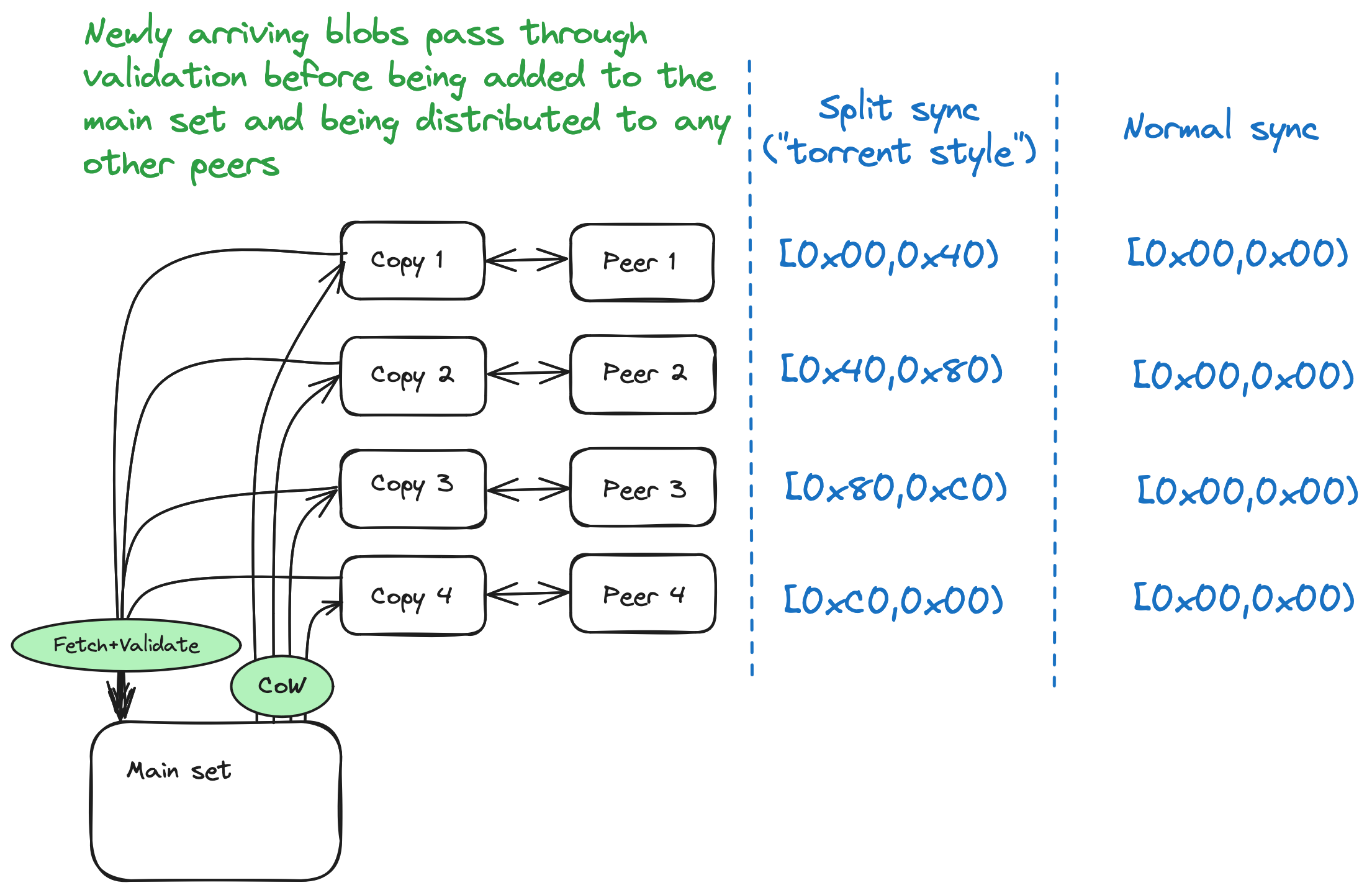
Due to the FPTree data structure being used, the copy operation on a
set is O(1). When synchronizing the local set against the remote
peer's set, we need to make sure the set doesn't change while being
synchronized, except for the recent items being added at the beginning
of the sync. Thus, for the purpose of synchronization against each
remote peer, a separate copy of the original set is made. When new
items are being received during sync with a remote peer, these items
are passed to the fetcher which retrieves the actual data blobs from
the peers, after which the received objects are validated and stored
in the state database. The main set is refreshed from time to time to
include the items that were recently added; this doesn't affect the
derived copies currently in use for sync.
When picking the peers for the purpose of multi-peer sync, each peer is probed to determine how many items it has in its set. The peers with substantially lower number of items than in the local set (configurable threshold) are not considered for sync, so as not to place additional load on the peer which are not fully synced yet, and let them decide on their syncing strategy on their own. Note that the sync is always bi-directional.
Synchronization against multiple peers can be done in two modes:
- Split sync involves splitting the whole range into smaller ones, one smaller range per peer, and limiting the sync to the corresponding range of IDs when syncing with each peer.
- Full sync involves syncing the full set against each peer's full set.
The sync strategy is selected based on the set similarity between the local peers and the peers that have been chosen for sync, as well as on the number of items in the remote peer sets. Roughly it can be described using the following diagram:
stateDiagram-v2
[*] --> Wait
Wait --> ProbePeers : Timeout
ProbePeers --> Wait : No peers / <br/> all probes failed
ProbePeers --> SplitSync : Enough peers for split + <br/> this one is too different + <br> last sync was not split
ProbePeers --> FullSync : Too few peers for split / <br/> this one is similar <br/> enough to peers
SplitSync --> Wait : Sync failed
SplitSync --> FullSync : Sync succeeded
FullSync --> Wait : Sync terminated
The split sync approach helps bringing nodes that went substantially out of sync relatively quickly while also making sure too much load is not placed on each of the syncing peers. It somewhat resembles BitTorrent approach where a file is downloaded from multiple peers, with different pieces being obtained from different peers, even if this similarity is rather superficial, as the protocol involved is very different. The split sync is followed by full sync against the peers, as in some cases, as with ATXs during cycle gaps, the set might became somewhat "outdated" while the sync was being done. Below is a diagram describing split sync sequence:
sequenceDiagram
Note over A: Check how different is A <br/> from its peers
par
A ->> B: Probe
B ->> A: Sample <br/> sim=0.95 count=10001
and
A ->> C: Probe
C ->> A: Sample <br/> sim=0.94 count=10002
and
A ->> D: Probe
D ->> A: Sample <br/> sim=0.94 count=10003
and
A ->> E: Probe
E ->> A: Sample <br/> sim=0.96 count=10001
and
A ->> F: Probe
F ->> A: Sample <br/> sim=0.89 count=9000
end
Note over A: Not enough peers close to this one <br/> Enough peers eligible for split sync <br/> Peer F's count is too low <br/> Proceeding with split sync
par
A <<->> B: Sync [0x00..., 0x40...)
and
A <<->> C: Sync [0x40..., 0x80...)
and
A <<->> D: Sync [0x80..., 0xC0...)
and
A <<->> E: Sync [0xC0..., 0x00...)
end
Note over A: Full sync follows split sync <br/> Syncing against peers that are in sync <br/> is very cheap
par
A <<->> B: Sync [0x00..., 0x00...)
and
A <<->> C: Sync [0x00..., 0x00...)
and
A <<->> D: Sync [0x00..., 0x00...)
and
A <<->> E: Sync [0x00..., 0x00...)
end
Note over A: Node A is in sync with the network
When some of the peers are too slow, their ranges are additionally assigned to faster peers that managed to complete their ranges already. Synchronization against slower peers is not interrupted though until each range is synced at least once:
sequenceDiagram
par
A <<->> B: Sync [0x00..., 0x40...)
and
A <<->> C: Sync [0x40..., 0x80...)
and
A <<->> D: Sync [0x80..., 0xC0...)
and
A <<->> E: Sync [0xC0..., 0x00...)
and
Note over A: Peer E being too slow
A <<->> E: Sync [0xC0..., 0x00...)
end
Full sync is used when this node's set is similar enough to its peers' sets, or when there's not enough peers for split sync. The full sync against each peer is more reliable than split sync against the same peers, so after split sync completes, full sync is always done. The diagram below illustrates the full sync sequence.
sequenceDiagram
Note over A: Check how different is A <br/> from its peers
par
A ->> B: Probe
B ->> A: Sample <br/> sim=0.999 count=10001
and
A ->> C: Probe
C ->> A: Sample <br/> sim=0.999 count=10002
and
A ->> D: Probe
D ->> A: Sample <br/> sim=0.999 count=10003
and
A ->> E: Probe
E ->> A: Sample <br/> sim=0.999 count=10001
and
A ->> F: Probe
F ->> A: Sample <br/> sim=0.090 count=9000
end
Note over A: Enough peers close to this one <br/> Peer F's count is too low <br/> Proceeding with full sync
par
A <<->> B: Sync [0x00..., 0x00...)
and
A <<->> C: Sync [0x00..., 0x00...)
and
A <<->> D: Sync [0x00..., 0x00...)
and
A <<->> E: Sync [0x00..., 0x00...)
end
Note over A: Node A is in sync with the network