参考:Most consistent ways of dealing with the series of stock problems
参考翻译:股票问题系列通解(转载翻译)
股票问题一共有六道题:
- 121. 买卖股票的最佳时机
- 122. 买卖股票的最佳时机 II
- 123. 买卖股票的最佳时机 III
- 188. 买卖股票的最佳时机 IV
- 309. 最佳买卖股票时机含冷冻期
- 714. 买卖股票的最佳时机含手续费
股票问题本质上是「状态机DP」
首先介绍一些符号:
- 用
n表示股票价格数组的长度; - 用
i表示第i天(i的取值范围是0到n - 1); - 用
maxK表示允许的最大交易次数;
假设用 dp[i][k] 表示在第 i 天结束时,进行 k 笔交易的情况下可以获得的最大收益。记录了 [0, i] 范围的最优解。
基础情况为 dp[i][0] = 0,表示没有进行股票交易时没有收益
如何进行状态转移:第 i 天可能的操作有三个:买入、卖出、休息,通过计算得到选择每个操作可以得到的最大收益
这里和参考中的定义不同,参考中定义第二维度为「最多」进行 k 笔交易,个人感觉直接定义为进行 k 笔交易清楚些
第二维度定义的不同,会引起初始化和答案返回的不同,一定要理解和注意
但是题目或者现实世界是有限制条件的,要符合逻辑
- 规定不能同时进行多次交易,因此如果决定在第
i天买入,在买入之前必须持有0份股票, - 如果决定在第
i天卖出,在卖出之前必须恰好持有1份股票。
因此用「第 i 天」和「当天结束后进行了 k 次交易」两个维度描述一个状态是不完整的
「当天结束后持有股票的数量」是第三个关键维度,该因素影响第 i 天可以进行的操作,进而影响最大收益。
因此对状态 dp 用三个维度重新状态定义:
dp[i][k][0]表示在第i天结束时,进行k笔交易且在进行操作后持有0份股票的情况下可以获得的最大收益;dp[i][k][1]表示在第i天结束时,进行k笔交易且在进行操作后持有1份股票的情况下可以获得的最大收益。
每次(笔)交易包含成对的操作:「买入」和「卖出」,仅当「买入」时会增加交易次数,一笔交易应该被理解为一次「交易周期」,买入会增加一次交易周期,而「卖出」只是将这次交易周期「闭环」,实际不会增加交易周期的次数
状态转移方程:
dp[i][k][0] = max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i])
dp[i][k][1] = max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i])-
dp[i][k][0],当前结束后持有的股票为0个,因此当天仅可进行「休息」和「卖出」操作,取两种操作的最大值- 当天「休息」,
dp[i - 1][k][0] - 当天「卖出」,
dp[i - 1][k][1] + prices[i],股票持有数从前一天的1减少到当前的0,由于是卖出操作不会影响到交易周期的次数,因此k不变,最后收益增加prices[i]
- 当天「休息」,
-
dp[i][k][1],当前结束后持有的股票为1个,因此当天仅可进行「休息」和「买入」操作,取两种操作的最大值- 当天「休息」,
dp[i - 1][k][1] - 当天「买入」,
dp[i - 1][k - 1][0] - prices[i],股票持有数从前一天的0增加到当前的1,由于是买入操作交易周期数从前一天的k-1次增加到当前的k笔,最后收益减少prices[i]
- 当天「休息」,
base case:初始化第 0 天的情况
dp[0][0][0] = 0,第0天没进行任何操作,收益为0dp[0][1][1] = -prices[0],第0天买了股票,收益为-prices[0]dp[0][k][j] = INT_MIN >> 1,类似这种第0天买了k次股票,不可能发生的事,用INT_MIN >> 1标记
INT_MIN除以2,是因为在遍历的过程中,dp记录的值会变得更小
获取答案:
由于我们将 dp[i][k][j] 定义为在第 i 天结束时,进行 k 笔交易后,获得的最大收益;
- 首先,一定是持有的股票数清
j = 0后的才能获得最大收益 - 其次,最后一天的最大收益,位于进行
k笔交易状态中的最大一个
所以,max{dp[n-1][k][0]...}
- 最后,由于初始化的时候引入了无穷小,结果可能是「负的」,代表一顿操作不如不买,这种情况返回
0
上述六个股票问题是根据 maxK 的值进行分类的,其中 maxK 是允许的最大交易次数。最后两个问题有附加限制,包括「冷冻期」和「手续费」。通解可以应用于每个股票问题。
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 10^50 <= prices[i] <= 10^4
0. 分析题目要求:
- 限制了最多 1 笔交易,仅有
dp[i][0][0]是有意义的,其他的dp[i][0][j]都无意义(仔细考虑下) - 因此,去掉第二个维度,用 0 替代
dp[i][0][0] - 不能同时参与多笔交易,手上可能存在 0 或 1 支股票
1. 定义状态
dp[i][0]第 i 天,当天结束后,持有股票数为 0 的最大利润([0, i]范围的最优解)dp[i][1]第 i 天,当天结束后,持有股票数为 1 的最大利润([0, i]范围的最优解)
2. 状态转移方程
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
dp[i][1] = max(dp[i - 1][1], 0 - prices[i])-
dp[i][0],当前结束后持有的股票为0个,因此当天仅可进行「休息」和「卖出」操作,取两种操作的最大值- 当天「休息」,
dp[i - 1][0] - 当天「卖出」,
dp[i - 1][1] + prices[i],股票持有数从前一天的1减少到当前的0,最后收益增加prices[i]
- 当天「休息」,
-
dp[i][1],当前结束后持有的股票为1个,因此当天仅可进行「休息」和「买入」操作,取两种操作的最大值- 当天「休息」,
dp[i - 1][1] - 当天「买入」,
0 - prices[i],收益减少prices[i]
- 当天「休息」,
问:这里为什么是用 0 减而不是 dp[i-1][0] ?
答:本题目要求,只能进行一次交易周期
- 因此在当天买入前不能进行交易,前一天的最大收益必然为
0 dp[i-1][0]代表了第i - 1天结束后,持有股票数为0,其中包含了前面的i-1天可能进行过交易,后来又卖出的情况- 如果真要用状态来计算的话,应该使用
dp[i-1][0][0],第i - 1天最大的交易次数为0次(不能交易)且持有股票数为0 - 而交易次数这个维度已经被消除掉了,故直接用 0 表示前面那些天不能交易的最大收益
3. 初始化
第 0 天的时候休息:dp[0][0] = 0
第 0 天的时候买入:dp[0][1] = -prices[i]
4. 输出
dp[n-1][0] 第 n-1 天,当天结束后,持有股票数为 0 的最大利润(肯定比最后一天手上还有股票的情况好)
空间优化
仅和前一天有关,可优化
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n) 或 O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]); // 当天 休息 或 卖
dp[i][1] = max(dp[i - 1][1], -prices[i]); // 当天 休息 或 买
}
return dp[n - 1][0];
}
};滚动数组:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int pre_zero = 0;
int pre_one = -prices[0];
for (int i = 1; i < n; i++) {
int cur_zero = max(pre_zero, pre_one + prices[i]); // 当天 休息 或 卖
int cur_one = max(pre_one, -prices[i]); // 当天 休息 或 买
pre_zero = cur_zero;
pre_one = cur_one;
}
return pre_zero;
}
};还有个模拟的算法:
提前算出当天前面那些天的最低股票
去模拟,前面最低的时候买,当前卖,记录整个过程中的最大值
时间复杂度:O(n)
空间复杂度:O(n)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n == 1) return 0;
// memo[i] 第i个元素前最低的股票价格,不包括prices[i]
vector<int> memo(n, 0);
memo[0] = INT_MAX;
for (int i = 1; i < n; i++) {
memo[i] = min(memo[i-1], prices[i-1]);
}
int ans = 0;
for (int i = 1; i < n; i++) {
if (prices[i] > memo[i]) {
ans = max(ans, prices[i] - memo[i]);
}
}
return ans;
}
};给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
提示:
1 <= prices.length <= 3 * 1040 <= prices[i] <= 104
0. 分析题目要求:
- 题目没有限制当天的交易次数,每天可进行无限次交易,第二个维度(当天交易的次数)就没了意义,不用了
- 不能同时参与多笔交易,手上可能存在 0 或 1 支股票
1. 定义状态
dp[i][0]第 i 天,当天结束后,持有股票数为 0 的最大利润([0, i]范围的最优解)dp[i][1]第 i 天,当天结束后,持有股票数为 1 的最大利润([0, i]范围的最优解)
2. 状态转移方程
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])-
dp[i][0],当前结束后持有的股票为0个,因此当天仅可进行「休息」和「卖出」操作,取两种操作的最大值- 当天「休息」,
dp[i - 1][0] - 当天「卖出」,
dp[i - 1][1] + prices[i],股票持有数从前一天的1减少到当前的0,最后收益增加prices[i]
- 当天「休息」,
-
dp[i][1],当前结束后持有的股票为1个,因此当天仅可进行「休息」和「买入」操作,取两种操作的最大值- 当天「休息」,
dp[i - 1][1] - 当天「买入」,
dp[i - 1][0] - prices[i],收益减少prices[i]
- 当天「休息」,
问:这里为什么又可以用 dp[i-1][0] ?
答:本题目整体上没有限制交易次数,只要确保手上最多只有一个股票就行
dp[i-1][0]代表了第i - 1天结束后,持有股票数为0,且包含了前面的i-1天可能进行过交易,后来又卖出的情况- 计算当天的最大收益,就得从前一天合理(股票清零)的最大收益转移过来
3. 初始化
第 0 天的时候休息:dp[0][0] = 0
第 0 天的时候买入:dp[0][1] = -prices[i]
4. 输出
dp[n-1][0] 第 n-1 天,当天结束后,持有股票数为 0 的最大利润(肯定比最后一天手上还有股票的情况好)
空间优化
仅和前一天有关,可优化
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n) 或 O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);
}
return dp[n-1][0];
}
};滚动数组:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int pre_zero = 0;
int pre_one = -prices[0];
for (int i = 1; i < n; i++) {
int cur_zero = max(pre_zero, pre_one + prices[i]);
int cur_one = max(pre_one, pre_zero - prices[i]);
pre_zero = cur_zero;
pre_one = cur_one;
}
return pre_zero;
}
};还有个贪心的做法:
贪心算法的直觉:由于不限制交易次数,只要今天股价比昨天高,就交易
该算法仅可以用于计算,但 计算的过程并不是真正交易的过程
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res = 0;
for (int i = 1; i < prices.size(); i++) {
if (prices[i] > prices[i - 1]) {
res += prices[i] - prices[i - 1];
}
}
return res;
}
};给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
输入:prices = [7,6,4,3,1]
输出:0
解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
输入:prices = [1]
输出:0
提示:
1 <= prices.length <= 1050 <= prices[i] <= 105
0. 分析题目要求:
- 限制了最多 2 笔交易
- 不能同时参与多笔交易,手上可能存在 0 或 1 支股票
1. 状态定义:
dp[i][k][j] 表示在 [0, i] 区间里(状态具有前缀性质),交易进行了 k 次,手上有 j 个股票时,拥有的最大收益。k 的含义如下:
k = 0表示没有交易发生;k = 1表示此时已经发生了 1 次买入股票的行为;k = 2表示此时已经发生了 2 次买入股票的行为。
注意:记录一次交易产生是在 买入股票 的时候。卖出时不变
2. 初始化(重点)
下标为 0 这一天,交易次数为 0、1、2 并且状态为 0 和 1 的初值应该如下设置:
dp[0][0][0] = 0:这是显然的;dp[0][0][1] = INT_MIN >> 1:表示一次交易都没有发生,但是持股,这是不可能的;dp[0][1][0] = INT_MIN >> 1:表示发生了 1 次交易(买入),但是不持股,这是不可能的;dp[0][1][1] = -prices[0]:表示发生了一次交易,并且持股,消耗了-prices[0];dp[0][2][0] = INT_MIN >> 1:表示发生了 2 次交易,但是不持股,这是不可能的;dp[0][2][1] = INT_MIN >> 1:表示发生了 2 次交易,第一天不可能发生两次交易;
一定要用「无穷小」标记不可能发生的事,用 0 记录收益为0,大于 0 记录产生了收益
通过 max 将无穷小的不可能发生的状态过滤掉
为什么「无穷小」还要除以二,往下看
3. 状态转移方程:
dp[i][1][0] = max(dp[i - 1][1][0], dp[i - 1][1][1] + prices[i]); // 当天 不操作、卖出
dp[i][1][1] = max(dp[i - 1][1][1], dp[i - 1][0][0] - prices[i]); // 当天 不操作、买入
dp[i][2][0] = max(dp[i - 1][2][0], dp[i - 1][2][1] + prices[i]); // 当天 不操作、卖出
dp[i][2][1] = max(dp[i - 1][2][1], dp[i - 1][1][0] - prices[i]); // 当天 不操作、买入注意:
- 第 2 维的 0 没有意义,遍历中不要算它的状态
- 当 i = 1时,
dp[i - 1][1][0] - prices[i]会让INT_MIN减一个正数,会报错,因此在初始化的时候一律除以二INT_MIN >> 1
4、获取答案:
到了最后一天 n-1,已完成的交易笔数可能进行了 1 次,也可能是 2 次,但是一定得手上的股票清空
返回 max(dp[n-1][1][0], dp[n-1][2][0]),但可能存在负值
表示如果交易的话一定会亏钱,不如不交易,返回 0
空间优化
滚动数组
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n) 或 O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<vector<int>>> dp(n, vector<vector<int>>(3, vector<int>(2, 0)));
// 第 2 维的 0 没有意义,1 表示交易进行了 1 次,2 表示交易进行了 2 次
dp[0][0][0] = 0;
dp[0][0][1] = INT_MIN >> 1;
dp[0][1][0] = INT_MIN >> 1;
dp[0][1][1] = -prices[0];
dp[0][2][0] = INT_MIN >> 1;
dp[0][2][1] = INT_MIN >> 1;
for (int i = 1; i < n; i++) {
dp[i][1][0] = max(dp[i - 1][1][0], dp[i - 1][1][1] + prices[i]); // 当天不操作,卖出
dp[i][1][1] = max(dp[i - 1][1][1], dp[i - 1][0][0] - prices[i]); // 当天不操作,买入
dp[i][2][0] = max(dp[i - 1][2][0], dp[i - 1][2][1] + prices[i]); // 当天不操作,卖出
dp[i][2][1] = max(dp[i - 1][2][1], dp[i - 1][1][0] - prices[i]); // 当天不操作,买入
}
int ans = max(dp[n - 1][1][0], dp[n - 1][2][0]);
return ans > 0 ? ans : 0;
}
};滚动数组:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<vector<int>>> dp(2, vector<vector<int>>(3, vector<int>(2, 0)));
dp[0][0][0] = 0;
dp[0][0][1] = INT_MIN >> 1;
dp[0][1][0] = INT_MIN >> 1;
dp[0][1][1] = -prices[0];
dp[0][2][0] = INT_MIN >> 1;
dp[0][2][1] = INT_MIN >> 1;
for (int i = 1; i < n; i++) {
dp[i & 1][1][0] = max(dp[(i - 1) & 1][1][0], dp[(i - 1) & 1][1][1] + prices[i]);
dp[i & 1][1][1] = max(dp[(i - 1) & 1][1][1], dp[(i - 1) & 1][0][0] - prices[i]);
dp[i & 1][2][0] = max(dp[(i - 1) & 1][2][0], dp[(i - 1) & 1][2][1] + prices[i]);
dp[i & 1][2][1] = max(dp[(i - 1) & 1][2][1], dp[(i - 1) & 1][1][0] - prices[i]);
}
int ans = max(dp[(n - 1) & 1][1][0], dp[(n - 1) & 1][2][0]);
return ans > 0 ? ans : 0;
}
};给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入:k = 2, prices = [2,4,1]
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
输入:k = 2, prices = [3,2,6,5,0,3]
输出:7
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
0 <= k <= 1000 <= prices.length <= 10000 <= prices[i] <= 1000
0. 分析题目要求:
- 指定了最多 k 次交易
- 不能同时参与多笔交易,手上可能存在 0 或 1 支股票
1. 状态定义:
dp[i][k][j] 表示在 [0, i] 区间里(状态具有前缀性质),交易进行了 k 次,手上有 j 个股票时,拥有的最大收益。
注意:记录一次交易产生是在 买入股票 的时候。卖出时不变
2. 初始化(重点)
下标为 0 这一天,交易次数为 0、1、2 并且状态为 0 和 1 的初值应该如下设置:
dp[0][0][0] = 0:这是显然的;dp[0][0][1] = INT_MIN >> 1:表示一次交易都没有发生,但是持股,这是不可能的;dp[0][1][0] = INT_MIN >> 1:表示发生了 1 次交易(买入),但是不持股,这是不可能的;dp[0][1][1] = -prices[0]:表示发生了一次交易,并且持股,消耗了-prices[0];dp[0][k][0] = INT_MIN >> 1, k>=2:第一天不可能发生两次以次上的交易;dp[0][k][1] = INT_MIN >> 1, k>=2:第一天不可能发生两次以次上的交易;
一定要用「无穷小」标记不可能发生的事,用 0 记录收益为0,大于 0 记录产生了收益
通过 max 将无穷小的不可能发生的状态过滤掉
3. 状态转移方程:
dp[i][k][0] = max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]); // 当天 不操作、卖出
dp[i][k][1] = max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]); // 当天 不操作、买入注意:
- 第 2 维的 0 没有意义,遍历中不要算它的状态
- 当 i = 1时,
dp[i - 1][1][0] - prices[i]会让INT_MIN减一个正数,会报错,因此在初始化的时候一律除以二INT_MIN >> 1 n天的股票,最多进行n / 2次交易,当指定的最多交易次数maxK大于n / 2,意味着交易次数不受限,应该转化为「交易笔数不受限制的做法」122 题,如果该按照本题的做法就会有错
4、获取答案:
到了最后一天 n-1,已完成的交易笔数可能进行了 k 次,但是一定得手上的股票清空
返回 max{dp[n-1][k][0]..},但可能存在负值
表示如果交易的话一定会亏钱,不如不交易,返回 0
空间优化
滚动数组
复杂度分析
时间复杂度:O(nk)
空间复杂度:O(nk) 或 O(k)
class Solution {
public:
int MIN = INT_MIN >> 1;
int specProfit(vector<int>& prices) {
int res = 0;
for (int i = 1; i < prices.size(); i++) {
if (prices[i] > prices[i - 1]) {
res += prices[i] - prices[i - 1];
}
}
return res;
}
int maxProfit(int k, vector<int>& prices) {
int maxK = k;
int n = prices.size();
if (maxK == 0) return 0;
if (maxK >= (n >> 1)) return specProfit(prices);
vector<vector<vector<int>>> dp(n, vector<vector<int>>(maxK + 1, vector<int>(2, 0)));
dp[0][0][0] = 0;
dp[0][0][1] = MIN;
dp[0][1][0] = MIN;
dp[0][1][1] = -prices[0];
for (int k = 2; k <= maxK; k++) {
dp[0][k][0] = MIN;
dp[0][k][1] = MIN;
}
for (int i = 1; i < n; i++) {
for (int k = 1; k <= maxK; k++) {
dp[i][k][0] = max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]); // 当天不操作,卖出
dp[i][k][1] = max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]); // 当天不操作,买入
}
}
int ans = 0;
for (int k = 0; k <= maxK; k++) {
ans = max(ans, dp[n - 1][k][0]);
}
return ans;
}
};滚动数组:
class Solution {
public:
int MIN = INT_MIN >> 1;
int specProfit(vector<int>& prices) {
int res = 0;
for (int i = 1; i < prices.size(); i++) {
if (prices[i] > prices[i - 1]) {
res += prices[i] - prices[i - 1];
}
}
return res;
}
int maxProfit(int k, vector<int>& prices) {
int maxK = k;
int n = prices.size();
if (maxK == 0) return 0;
if (maxK >= (n >> 1)) return specProfit(prices);
vector<vector<vector<int>>> dp(2, vector<vector<int>>(maxK + 1, vector<int>(2, 0)));
dp[0][0][0] = 0;
dp[0][0][1] = MIN;
dp[0][1][0] = MIN;
dp[0][1][1] = -prices[0];
for (int k = 2; k <= maxK; k++) {
dp[0][k][0] = MIN;
dp[0][k][1] = MIN;
}
for (int i = 1; i < n; i++) {
for (int k = 1; k <= maxK; k++) {
dp[i & 1][k][0] = max(dp[(i - 1) & 1][k][0], dp[(i - 1) & 1][k][1] + prices[i]);
dp[i & 1][k][1] = max(dp[(i - 1) & 1][k][1], dp[(i - 1) & 1][k - 1][0] - prices[i]);
}
}
int ans = 0;
for (int k = 0; k <= maxK; k++) {
ans = max(ans, dp[(n - 1) & 1][k][0]);
}
return ans;
}
};给定一个整数数组prices,其中第 prices[i] 表示第 *i* 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
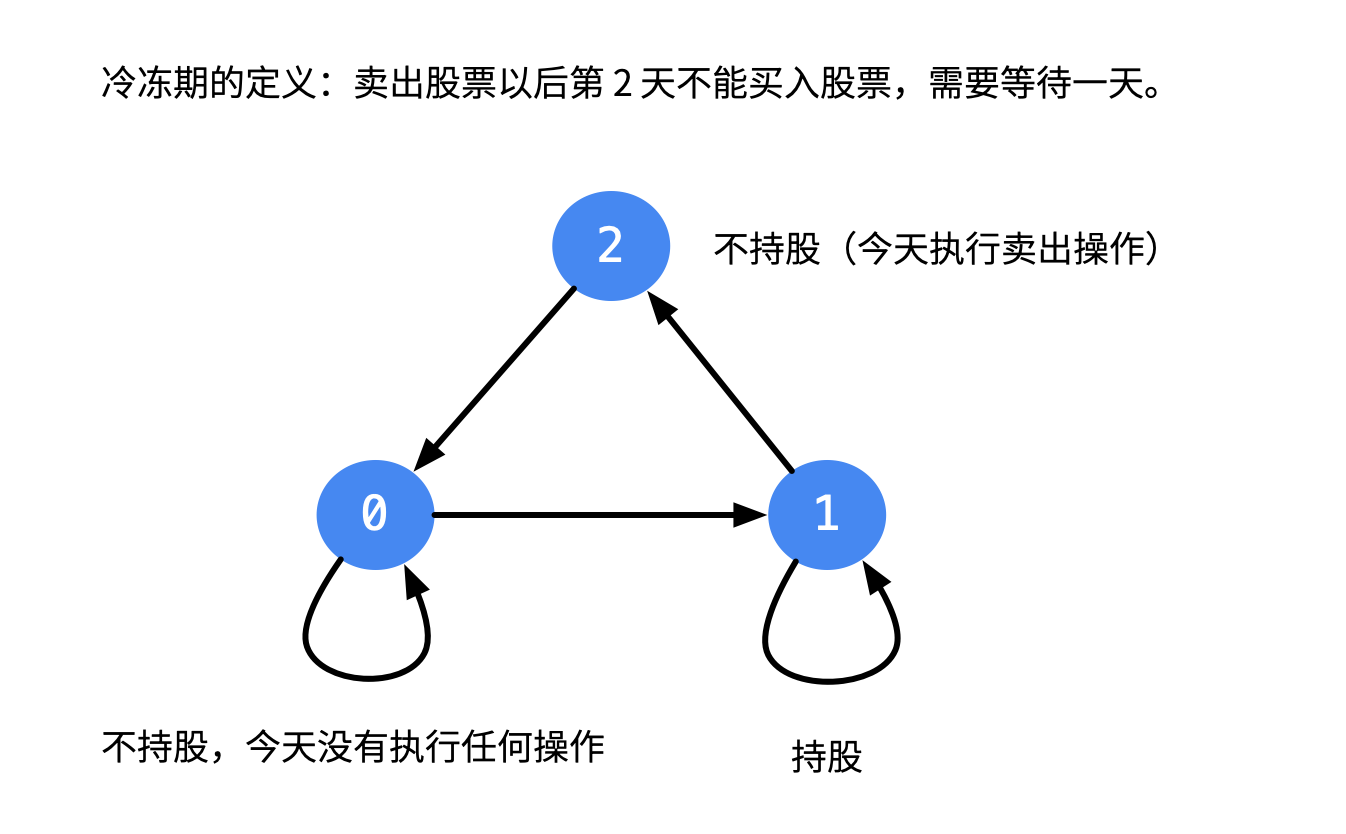
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
输入: prices = [1]
输出: 0
提示:
1 <= prices.length <= 50000 <= prices[i] <= 1000
0. 分析题目要求:
- 交易次数不受限制,类似情况 2,不用交易次数维度
- 不能同时参与多笔交易,手上可能存在 0 或 1 支股票
- 卖出股票会有冷冻期,所以当天要买入的话,得从前一天没有卖出的状态转移过来
1. 定义状态
dp[i][j] 表示 [0, i] 区间内,在下标为 i 这一天状态为 j 时,我们手上拥有的金钱数。
这里 j 可以取 3 个值(下面的定义非常重要):
0表示:今天 不是 卖出了股票的不持股状态;1表示:持股;2表示:今天由于卖出了股票的不持股状态;
2. 状态转移
根据题意,从昨天到今天可能的状态变化分析如下:
- 0 的转移
| 昨天 | 今天 | 分析是否可以转移,可以转移的情况下今天的操作 |
|---|---|---|
| 0 | 0 | 可以转移,今天什么都不做 |
| 0 | 1 | 可以转移,今天买入股票 |
| 0 | 2 | 不可以转移,不持股的情况下,不能卖出股票 |
- 1 的转移
| 昨天 | 今天 | 分析是否可以转移,可以转移的情况下今天的操作 |
|---|---|---|
| 1 | 0 | 不可以转移,根据题意,只能转移到 2 |
| 1 | 1 | 可以转移,今天什么都不操作 |
| 1 | 2 | 可以转移,当天卖出后转为「卖出不持股状态」 |
- 2 的转移
| 昨天 | 今天 | 分析是否可以转移,可以转移的情况下今天的操作 |
|---|---|---|
| 2 | 0 | 可以转移,昨天为「卖出不持股状态」,今天结束后冷却期过去了 |
| 2 | 1 | 不可以转移,昨天为「卖出不持股状态」,今天不能买入 |
| 2 | 2 | 不可以转移,不合逻辑 |
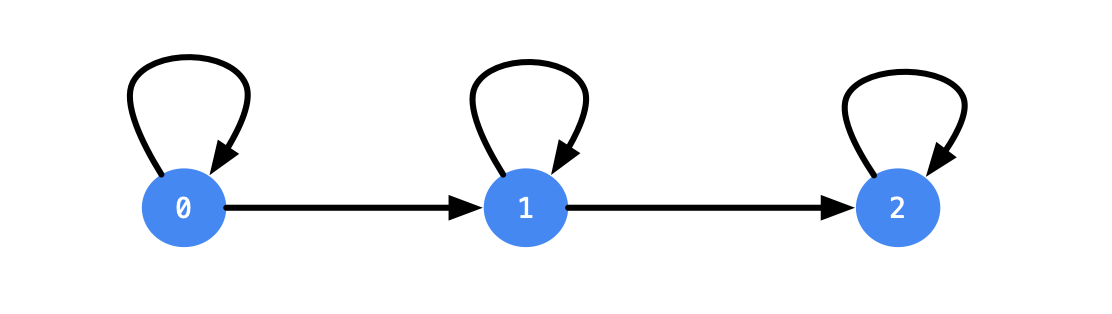
可以画出状态转移的图如下:
3. 初始化
第 0 天的时候休息:dp[0][0] = 0
第 0 天的时候买入:dp[0][1] = -prices[i]
第 0 天冷却期:dp[0][2] = 0,这里其实也可用 INT_MIN >> 1 ,但最后得判断下正负
4. 输出
max(dp[n-1][0], dp[n-1][2])
第 n-1 天,当天结束后,持有股票数为 0 的最大利润,可能是早都卖了,也可能刚卖进入cd
空间优化
仅和前一天有关,可优化,滚动数组
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n) 或 O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(3, 0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][2]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = dp[i - 1][1] + prices[i];
}
return max(dp[n - 1][0], dp[n - 1][2]);
}
};滚动数组:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(2, vector<int>(3, 0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;
for (int i = 1; i < n; i++) {
dp[i & 1][0] = max(dp[(i - 1) & 1][0], dp[(i - 1) & 1][2]);
dp[i & 1][1] = max(dp[(i - 1) & 1][1], dp[(i - 1) & 1][0] - prices[i]);
dp[i & 1][2] = dp[(i - 1) & 1][1] + prices[i];
}
return max(dp[(n - 1) & 1][0], dp[(n - 1) & 1][2]);
}
};给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
**注意:**这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
输入:prices = [1, 3, 2, 8, 4, 9], fee = 2
输出:8
解释:能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
输入:prices = [1,3,7,5,10,3], fee = 3
输出:6
提示:
1 <= prices.length <= 5 * 10^41 <= prices[i] < 5 * 10^40 <= fee < 5 * 104
0. 分析题目要求:
- 交易次数不受限制,类似情况 2,不用交易次数维度
- 不能同时参与多笔交易,手上可能存在 0 或 1 支股票
- 卖出股票会手续费
1. 定义状态
dp[i][j] 表示 [0, i] 区间内,在下标为 i 这一天状态为 j 时,我们手上拥有的金钱数。
2. 状态转移
与情况 2 不同的情况在于,卖出的时候叫上手续费
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);3. 初始化
第 0 天的时候休息:dp[0][0] = 0
第 0 天的时候买入:dp[0][1] = -prices[i]
4. 输出
dp[n-1][0] 第 n-1 天,当天结束后,持有股票数为 0 的最大利润(肯定比最后一天手上还有股票的情况好)
空间优化
仅和前一天有关,可优化
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n) 或 O(1)
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
};滚动数组:
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
vector<vector<int>> dp(2, vector<int>(2, 0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[i & 1][0] = max(dp[(i - 1) & 1][0], dp[(i - 1) & 1][1] + prices[i] - fee);
dp[i & 1][1] = max(dp[(i - 1) & 1][1], dp[(i - 1) & 1][0] - prices[i]);
}
return dp[(n - 1) & 1][0];
}
};