Project 3: Word Search

Partner Project: Andrew Tu, Haley Weinstein

Usage

• run make to build the Driver executable.
• Executable will be produced in the release folder.
• The executable in the timing folder will run all sort functions on all grids using the wordlist2.cpp as input.
• The executable in the debug folder has been compiled with debugging flags...
• You will be prompted to enter the file names for the grid file, the wordlist file and the sort mechanism you wish to use.

Make sure the name you enter is valid: We do not check whether the name you give is a valid name. If you provide an invalid name, the program will likely hang. You can use the files from the data directory. Give the realtive path name. i.e. "data/input250.txt"

• Sorts are as following
  1. Insertion
  2. Quick
  3. Merge
  4. STL
  5. Hash
  6. Heap

Performance

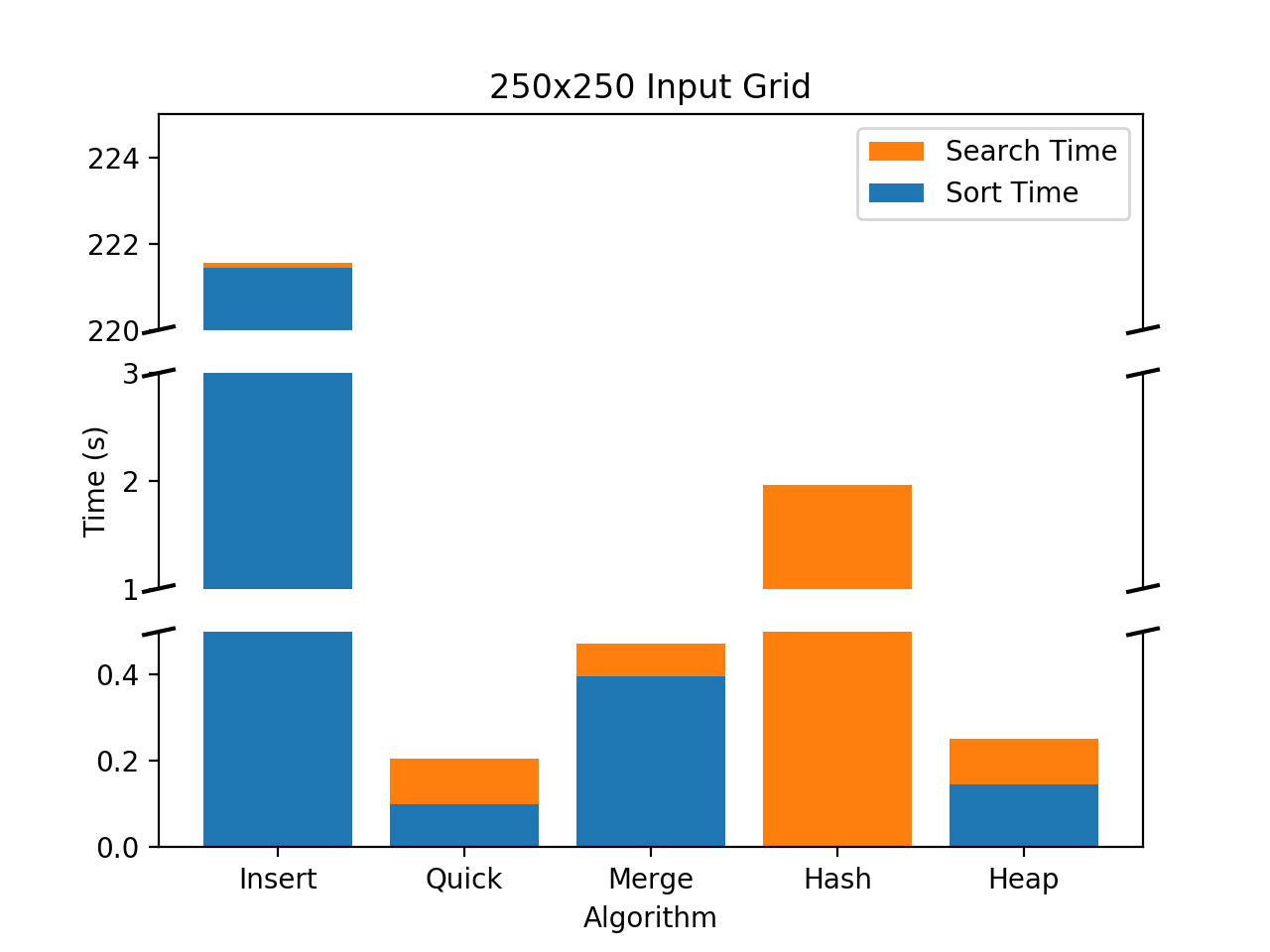
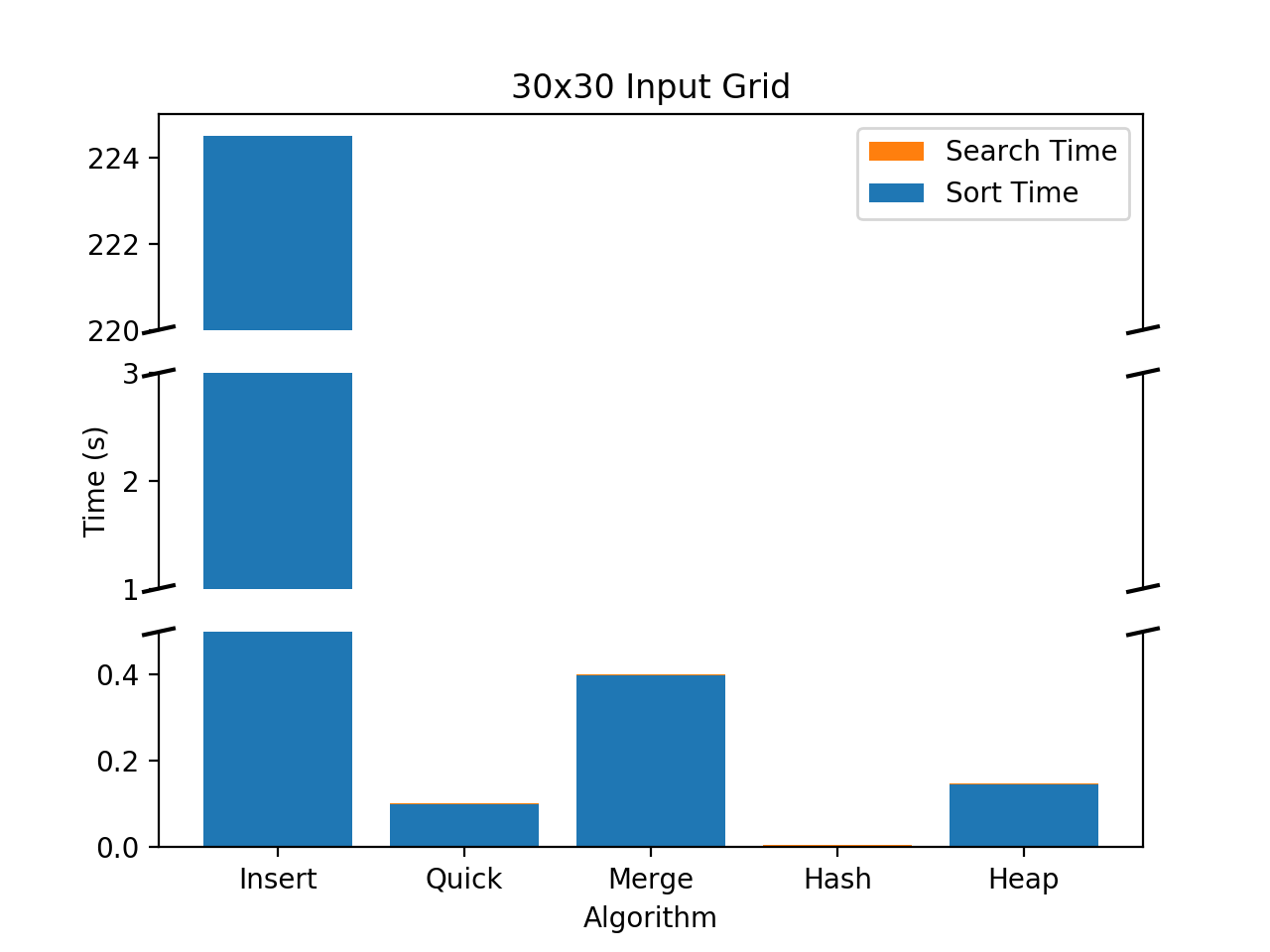
Timing data was collected for all sorting mechanisms on all grids using the wordlist2.txt file (approx 90k words). The results of each sorting algorithm can be seen in the following figure.

The tests were run on a machine running Ubuntu 16.04 with 2 Intel Xeon X5650 processors (total of 24 cores @ 2.67 Ghz). Multithreading was achieved using 24
OpenMP threads.

We saw a range of performances on total run time depending on the sorting algorithm used. Total run time was calculated as the Ttotal = Tsort + Tsearch. In the following sections, we explain differences in performances in the sort and search times.

Sort

Each of the sorting algorithms behaved as expected. Insertion sort ran very slowly ranging from 221.45 to 224.493 seconds whereas the quicksort ran in the range from .100246 to .100391 seconds and merge ran slightly slower than quicksort at .395506 to .3999265 seconds. This timing reflects the calculated different average case time scenarios.

Hashing did not need to sort the data, thus its value can be interpretted as 0.

Search

The high level view of our searching algorithm is as follows. For each character in our grid, search all 8 directions for words starting with that character. For an NxN grid, this costs roughly N^3*8(Lookup) where "Lookup" is the cost to determine if a given word exists within our word list. This meant that as the problem size scaled, search times would far outstrip sort times (the highest of which was X^2, if X is the size of a given wordList). This was also observed empirically where sorting wordlist2 took ~200s and (single threaded) searching took ~350 seconds.

Results

For algorithms where we organized data by sorting, we were able to significantly reduce our search time by performing lookups to see if words starting with a given string existed in our wordlist. If no word with existed with the gvien stem, we could stop searching a given direction and continue on the next direction. For example, if the first 3 letters of a sequence were "xyz", and there weren't any words in our wordlist that started with "xyz", we could safely stop searching for more words in this direction. In the case of the 250x250 grid, this meant not having to perform 247 more searches. Emplying this optimization saw a 230x improvement.

Because we cannot perform a similar optimzation with our hash table, our search using a hash table must search through the entire 250x250 grid. This difference in performance is shown in the algorithmic complexity of the two searching algoritms: the unsorted serach algorithm will always perform in n^3 time while the sorted algorithm ranges from best case n^2 time to worst case n^3.

Threading vs Algorithmic Complexity

This project also demonstrated an important concept in scalability. We improved performance by decreasing algorithmic complexity and by parallelizing our search algorithm. If we look at the impact each of these improvments had, we see that the perforamnce increase gained by improving our algorithmic complexity far outstrips the performance boost from multithreading.

By reducing the algorithmic complexity of the program, we reduce the amount of work we our program needs to do. By adding multithreading, we increase the amount of work our program can do per unit time. As our problem sizes grow larger and larger, the impact of reducing the work we need to do by a factor of n outstrips the speedup gained by multithreading. Furthermore, the speedup gained by multithreading any applciation is limited by the number of available cores.

TODO: Figure on performance