Name		Name	Last commit message	Last commit date
parent directory ..
Bubble_Sort.c		Bubble_Sort.c
Bubble_Sort.coffee		Bubble_Sort.coffee
Bubble_Sort.cpp		Bubble_Sort.cpp
Bubble_Sort.cs		Bubble_Sort.cs
Bubble_Sort.java		Bubble_Sort.java
Bubble_Sort.js		Bubble_Sort.js
Bubble_Sort.php		Bubble_Sort.php
Bubble_Sort.py		Bubble_Sort.py
Bubble_Sort.rb		Bubble_Sort.rb
README.md		README.md

README.md

BUBBLE SORT

Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order. It makes multiple passes through a list, compares adjacent items and exchanges those that are out of order. Each pass through the list places the next largest value in its proper place.

EXAMPLE

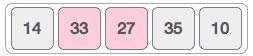
Given below is an unsorted array. Bubble sort takes Ο(n^2) time.

Bubble sort starts with very first two elements, comparing them to check which one is greater.

In this case, value 33 is greater than 14, so it is already in sorted locations. Next, we compare 33 with 27.

We find that 27 is smaller than 33 and these two values must be swapped.

The new array should look like this −

Next we compare 33 and 35. We find that both are in already sorted positions.

Then we move to next two values, 35 and 10.

We know than 10 is smaller 35. Hence they are not sorted.

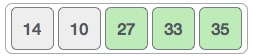
We swap these values. We find that we reach at the end of the array. After one iteration the array should look like this −

To be precise, we are now showing that how array should look like after each iteration.

After second iteration, it should look like this −

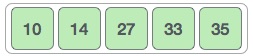
Notice that after each iteration, at least one value moves at the end.

And when there's no swapping required, bubble sorts learns that array is completely sorted.

PSEUDOCODE

We use one flag variable swapped which will help us to see if any swap is happened or not. If no swap is occurred, i.e. the array requires no more processing to be sorted, it will come out of the loop.

Pseudocode of BubbleSort algorithm can be expressed as −

procedure bubbleSort(list : array of items)

    loop = list.count;

    for i = 0 to loop-1 do:
        swapped = false

        for j = 0 to loop-i-1 do:

            /* compare the adjacent elements */
            if list[j] > list[j+1] then
                /* swap them */
                swap(list[j], list[j+1])
                swapped = true
            end if

        end for

        /*if no number was swapped that means
        array is sorted now, break the loop.*/

        if(not swapped) then
            break
        end if
    end for

end procedure and return list