WARNING: FOOOF is not yet tagged for a stable release version, and updates may change the internal workings, and/or the API (although major changes to API are unlikely). Prior to tagged release, tutorials may not be kept entirely up to date, but in-file documentation will be.
FOOOF is a fast, efficient, physiologically-informed model to parameterize neural power spectra.
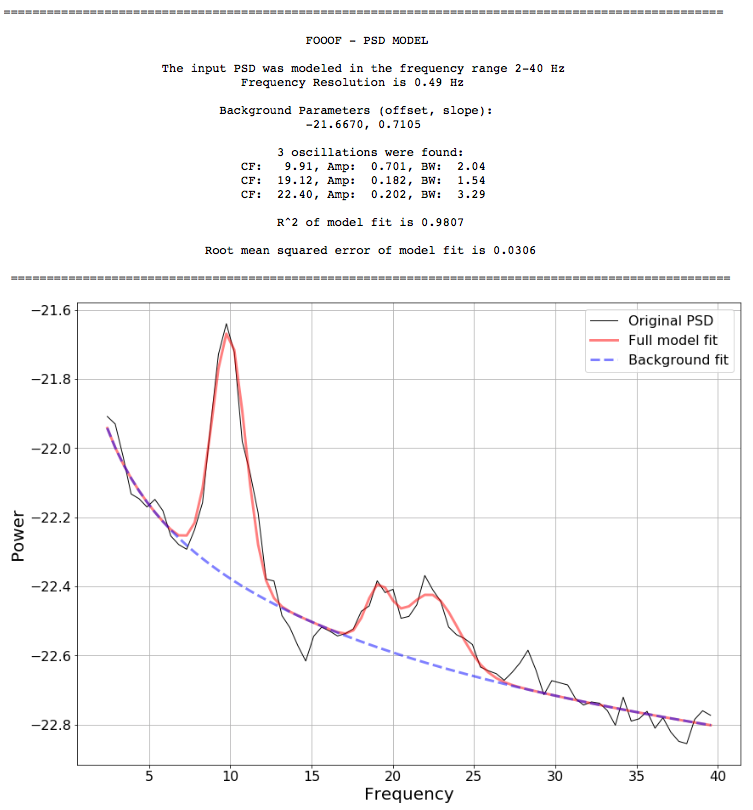
The model conceives of the neural power spectral density (PSD) as consisting of two distinct functional processes: 1) A 1/f background modeled as a curve in log-log space with; 2) Band-limited oscillatory "bumps" rising above this background, modeled as Gaussians in log(power) space.
Note that this conception of the 1/f as potentially functional (and therefore worth carefully modeling) is based on work from our lab suggesting that the 1/f slope may index excitation/inhibition balance (Gao, Peterson, Voytek, NeuroImage 2017; Voytek & Knight, Biol Psychiatry 2015). At the very least, however, the 1/f appears to change with task (Podvalny et al., J Neurophysiol 2015), with aging (Voytek et al., J Neurosci 2015).
FOOOF is written and tested in Python 3.6. It is not currently tested or supported on earlier versions (but should work on earlier versions of Python3 and should be compatible with Python2.7)
- numpy
- matplotlib
- scipy >= 0.19
FOOOF is object oriented. With a power spectrum loaded (with 'freqs' storing frequency values, and 'psd' storing power values, both as 1D arrays in linear space) FOOOF can be used as follows:
from fooof import FOOOF
# Initialize FOOOF object
foof_model = FOOOF()
# Define frequency range to model PSD
freq_range = [3, 40]
# Model the PSD with FOOOF
foof_model.model(freqs, psd, freq_range)FOOOF.model() fits the model, plots the original PSD with the associated model of the PSD, and prints out the parameters of the model fit for both background 1/f (offset, knee, exponent) and Gaussian parameters (center frequency, amplitude, and bandwidth) for any identified oscillations.
FOOOF also accepts parameters for fine-tuning the fit. For example:
foof_model = FOOOF(bandwidth_limits=(1.0,15.0), max_n_oscs=6, min_amp=0.1, amp_std_thresh=2.0)- bandwidth_limits sets the possible lower- and upper-bounds for the fitted Gaussians bandwidths to 1.0 and 15.0 Hz, respectively.
- max_n_oscs sets the maximum number of oscillations to find (in decreasing order of amplitude). Physiologically, rarely are there ever more than 5 or 6. This helps minimize overfitting.
- min_amp sets a hard limit on the maximum amplitude (above background 1/f) for any oscillation; that is, bumps below this amplitude will be ignored.
- amp_std_thresh, similar to min_amp, sets a threshold above which oscillation amplitude must cross to be included in the model. However this parameter is in terms of standard deviation above the noise of the flattened spectrum.