Skip to content

Latest commit

 

History

History
1775 lines (1283 loc) · 45.3 KB

2024-06-26-CALCN.md

File metadata and controls

1775 lines (1283 loc) · 45.3 KB
title date categories math comments
CALCOLO 2024
2024-05-05 16:00:00 -0700
UNIVERSITY
true
true

CALCOLO NUMERICO

{: .prompt-tip }

for those who are english speakers, I don't know if my teacher wants this documentation in english or italian, so I'll write it in italian you can translate it with google translate or something like that.

Questo è un riassunto di tutti i codici di calcolo numerico che ho scritto durante il corso di calcolo numerico all'università di Bari.

{: .prompt-info }

Potete trovare tutti i codici qui!

INDEX

Ritrovamento degli zeri di una funzione

$$ f(x) = 0 \space ? $$

Metodo delle bisezioni

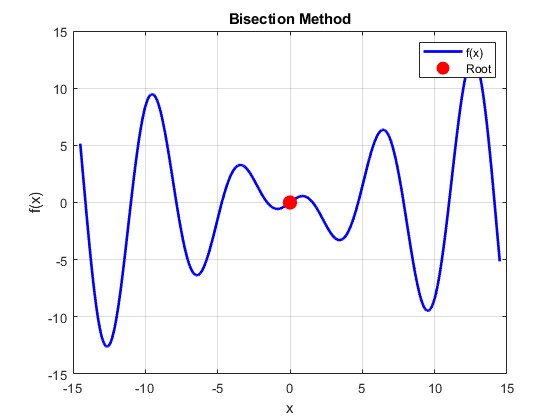
Il metodo di bisezione è un metodo di ricerca di zeri di una funzione continua in un intervallo.

Il metodo prevede di dividere l'intervallo in due parti uguali e di selezionare il sottointervallo in cui la funzione soddisfi il teorema degli zero.

Questo processo viene ripetuto fino a quando la lunghezza dell'intervallo diventa sufficientemente piccola.

Formalmente il metodo può essere descritto come segue:

  1. Scegliere un intervallo iniziale $$[a, b]$$ tale che $$ f(a) * f(b) < 0 \space$$ a.k.a teorema degli zeri o di Bolzano
  2. Calcolare il punto medio $$ c = (a + b) / 2 $$
  3. Calcolare $$ f(c) $$
  4. Se $$ f(c) = 0 $$ , allora $$ c $$ è la radice
  5. Altrimenti, se $$ f(c) * f(a) < 0 $$ , allora la radice si trova nell'intervallo $$ [a, c] $$
  6. Altrimenti, la radice si trova nell'intervallo $$ [c, b] $$
  7. Ripetere i passaggi 2-6 fino a quando la lunghezza dell'intervallo diventa più piccola di una certa tolleranza
function  m = bisection(f, low, high, tol , cap)
disp('Bisection Method'); 

y1 = feval(f, low);
y2 = feval(f, high);
i = 0; 

if y1 * y2 > 0
   disp('Bolzano theorem not verified ...');
   m = 'Error';
   return
end 

disp('Iter    low        high          x0');
while (abs(high - low) >= tol)
    i = i + 1;
    
    m = (high + low)/2;
    y3 = feval(f, m);
    if y3 == 0
        fprintf('Root at x = %f \n\n', m);
        return
    end
    fprintf('%2i \t %f \t %f \t %f \n', i-1, low, high, m);   

    if y1 * y3 > 0
        low = m;
        y1 = y3;
    else
        high = m;
    end

    if i > cap
        break
    end 
    
end 

fprintf('\n x = %f produces f(x) = %f \n %i iterations\n', m, y3, i-1);
fprintf(' Approximation with tolerance = %f \n', tol);

Il codice scritto calcola la radice di una funzione $$ f $$ nell'intervallo $$ [low, high] $$ con una tolleranza $$ tol $$ e un limite di iterazioni $$ cap $$

{: .prompt-info}

Esempio di utilizzo del codice:

f = @(x)(x+1)^2-4;
bisection(f,-3,4,0.00000001 , 100);

{: .prompt-tip}

Dando come output:

Bisection Method
Iter         low           high            x0
 0 	 -3.000000 	 4.000000 	 0.500000 
 1 	 -3.000000 	 0.500000 	 -1.250000 
 2 	 -3.000000 	 -1.250000 	 -2.125000 
 3 	 -3.000000 	 -2.125000 	 -2.562500 
 4 	 -3.000000 	 -2.562500 	 -2.781250 
 5 	 -3.000000 	 -2.781250 	 -2.890625 
 6 	 -3.000000 	 -2.890625 	 -2.945312 
 7 	 -3.000000 	 -2.945312 	 -2.972656 
 8 	 -3.000000 	 -2.972656 	 -2.986328 
 9 	 -3.000000 	 -2.986328 	 -2.993164 
10 	 -3.000000 	 -2.993164 	 -2.996582 
11 	 -3.000000 	 -2.996582 	 -2.998291 
12 	 -3.000000 	 -2.998291 	 -2.999146 
13 	 -3.000000 	 -2.999146 	 -2.999573 
14 	 -3.000000 	 -2.999573 	 -2.999786 
15 	 -3.000000 	 -2.999786 	 -2.999893 
16 	 -3.000000 	 -2.999893 	 -2.999947 
17 	 -3.000000 	 -2.999947 	 -2.999973 
18 	 -3.000000 	 -2.999973 	 -2.999987 
19 	 -3.000000 	 -2.999987 	 -2.999993 
20 	 -3.000000 	 -2.999993 	 -2.999997 
21 	 -3.000000 	 -2.999997 	 -2.999998 
22 	 -3.000000 	 -2.999998 	 -2.999999 
23 	 -3.000000 	 -2.999999 	 -3.000000 
24 	 -3.000000 	 -3.000000 	 -3.000000 
25 	 -3.000000 	 -3.000000 	 -3.000000 
26 	 -3.000000 	 -3.000000 	 -3.000000 
27 	 -3.000000 	 -3.000000 	 -3.000000 
28 	 -3.000000 	 -3.000000 	 -3.000000 
29 	 -3.000000 	 -3.000000 	 -3.000000 

 x = -3.000000 produces f(x) = -0.000000 
 29 iterations
 Approximation with tolerance = 0.000000

{: .prompt-tip}

Plot della funzione $$ f(x):=x*cos(x)$$

plot

Metodo Regula Falsi

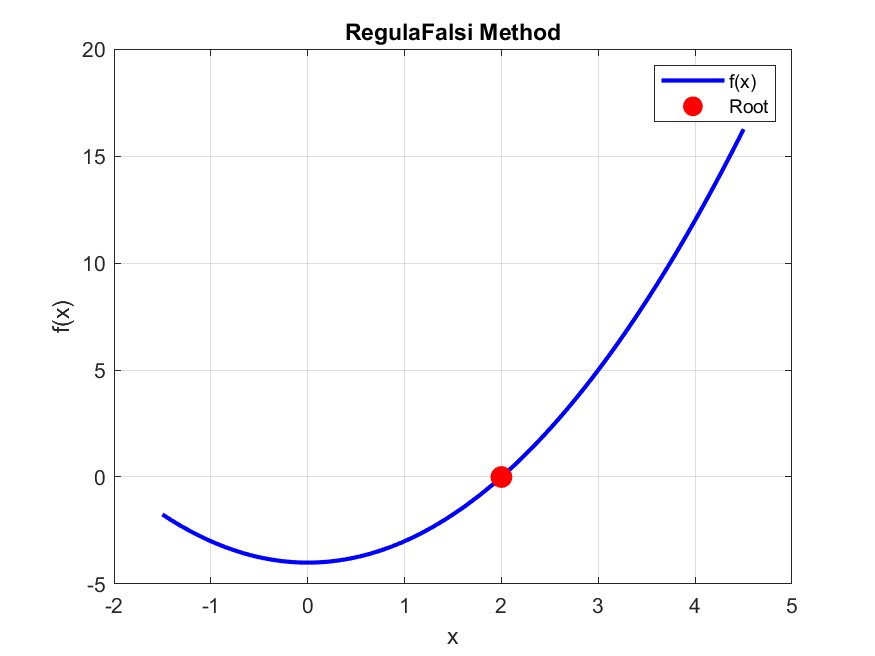
Il metodo della Regula Falsi è un metodo di ricerca di zeri di una funzione continua in un intervallo.

Esso è una variante del metodo delle bisezioni, in cui il punto medio viene calcolato come l'intersezione della retta che passa per $$ (a, f(a)) $$ e $$ (b, f(b)) $$ con l'asse x.

Il metodo della Regula Falsi può essere descritto come segue:

  1. Scegliere un intervallo iniziale $$[a, b]$$ tale che $$ f(a) * f(b) < 0 $$ teorema di Bolzano
  2. Calcolare il punto medio $$ c = a - f(a) * \dfrac{(b - a)}{(f(b) - f(a))} $$
  3. Calcolare $$ f(c) $$
  4. Se $$ f(c) = 0 $$ , allora $$ c $$ è la radice
  5. Altrimenti, se $$ f(c) * f(a) < 0 $$ , allora la radice si trova nell'intervallo $$ [a, c] $$
  6. Altrimenti, la radice si trova nell'intervallo $$ [c, b] $$
  7. Ripetere i passaggi 2-6 fino a quando la lunghezza dell'intervallo diventa più piccola di una certa tolleranza
function m = falsePosition(f, low , high , tol , cap)
disp('falsePosition');

y1 = feval(f, low);
y2 = feval(f, high);
i = 0; 

if y1 * y2 > 0
   disp('Bolzano theorem not verified ...');
   m = 'Error';
   return
end

disp('Iter    low        high          x0');
while (abs(high - low) >= tol)
    i = i + 1;
    
    m = low - y1 * (high - low) / (y2 - y1);

    y3 = feval(f,m);

    if y3 == 0
        fprintf('Root at x = %f \n\n', m);
        return
    end
    fprintf('%2i \t %f \t %f \t %f \n', i-1, low, high, m);   

    if y1 * y3 > 0
        low = m;
        y1 = y3;
    else
        high = m;
    end

    if i > cap
        break
    end 
end 

fprintf('\n x = %f produces f(x) = %f \n %i iterations\n', m, y3, i-1);
fprintf(' Approximation with tolerance = %f \n', tol);

Il codice scritto segue lo stesso principio del metodo delle bisezioni, ma invece di calcolare il punto medio, calcola il punto in cui la retta che passa per $$ (a, f(a)) $$ e $$ (b, f(b)) $$ interseca l'asse x.

{: .prompt-info}

Esempio di utilizzo del codice:

f = @(x)(x+1)^2-10;
falsePosition(f,-4,10,0.00000001, 100);

{: .prompt-tip}

Dando come output:

falsePosition
Iter      low              high            x0
 0 	 -4.000000 	 10.000000 	 -3.875000 
 1 	 -3.875000 	 10.000000 	 -3.661538 
 2 	 -3.661538 	 10.000000 	 -3.311808 
 3 	 -3.311808 	 10.000000 	 -2.775961 
 4 	 -2.775961 	 10.000000 	 -2.033774 
 5 	 -2.033774 	 10.000000 	 -1.137616 
 6 	 -1.137616 	 10.000000 	 -0.218751 
 7 	 -0.218751 	 10.000000 	 0.578248 
 8 	 0.578248 	 10.000000 	 1.175242 
 9 	 1.175242 	 10.000000 	 1.575107 
10 	 1.575107 	 10.000000 	 1.823269 
11 	 1.823269 	 10.000000 	 1.970061 
12 	 1.970061 	 10.000000 	 2.054437 
13 	 2.054437 	 10.000000 	 2.102138 
14 	 2.102138 	 10.000000 	 2.128853 
15 	 2.128853 	 10.000000 	 2.143736 
16 	 2.143736 	 10.000000 	 2.152003 
17 	 2.152003 	 10.000000 	 2.156587 
18 	 2.156587 	 10.000000 	 2.159127 
19 	 2.159127 	 10.000000 	 2.160534 
20 	 2.160534 	 10.000000 	 2.161312 
21 	 2.161312 	 10.000000 	 2.161743 
22 	 2.161743 	 10.000000 	 2.161982 
23 	 2.161982 	 10.000000 	 2.162114 
24 	 2.162114 	 10.000000 	 2.162187 
25 	 2.162187 	 10.000000 	 2.162228 
26 	 2.162228 	 10.000000 	 2.162250 
27 	 2.162250 	 10.000000 	 2.162262 
28 	 2.162262 	 10.000000 	 2.162269 
29 	 2.162269 	 10.000000 	 2.162273 
30 	 2.162273 	 10.000000 	 2.162275 
31 	 2.162275 	 10.000000 	 2.162276 
32 	 2.162276 	 10.000000 	 2.162277 
33 	 2.162277 	 10.000000 	 2.162277 
34 	 2.162277 	 10.000000 	 2.162277 
35 	 2.162277 	 10.000000 	 2.162278 
36 	 2.162278 	 10.000000 	 2.162278 
37 	 2.162278 	 10.000000 	 2.162278 
38 	 2.162278 	 10.000000 	 2.162278 
39 	 2.162278 	 10.000000 	 2.162278 
40 	 2.162278 	 10.000000 	 2.162278 

x = 2.162278 produces f(x) = -0.000000 
40 iterations
Approximation with tolerance = 0.000000

{: .prompt-tip}

Plot della funzione $$ f(x):=x^2 - 4$$

plot

Metodo di Newton

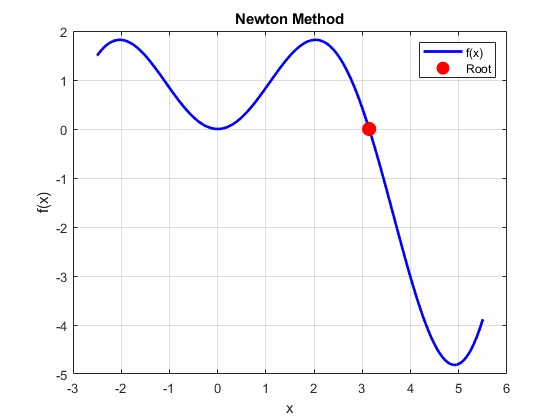
Il metodo di Newton è un metodo iterativo per trovare gli zeri di una funzione.

Il metodo di Newton è basato sull'idea di approssimare la funzione con una retta tangente e trovare il punto in cui la retta tangente interseca l'asse x.

Il metodo di Newton può essere descritto come segue:

  1. Scegliere un punto iniziale $$ x_0 $$
  2. Calcolare la derivata della funzione $$ f'(x) $$
  3. Calcolare il punto in cui la retta tangente interseca l'asse x: $$ x_1 = x_0 - \dfrac{f(x_0)}{f'(x_0)} $$
  4. Ripetere i passaggi 2-3 fino a quando la differenza tra $$ x_n $$ e $$ x_{n-1} $$ è inferiore a una certa tolleranza stando attenti a non dividere per un valore troppo piccolo e a non superare un certo numero di iterazioni
function m = newton(f, g, x0, tol, cap)

i = 1;
m = x0;

dm = - f(m) / g(m);


disp('Iter x0');
while abs(dm) > tol 

    if i > cap
        disp("iteration limit reached")
        m = "Error";
        return 
    end 

    if abs(g(m)) < 10^-10 
        disp("the value of g(x) is too small")
        m = "Error";
        return 
    end 

    m  = m + dm;
    fprintf("%i \t %f \n", i, m)
    

    dm = - f(m) / g(m);
    i = i + 1;
end 

fprintf('\n x = %f produces f(x) = %f \n %i iterations\n', m, feval(f,m), i-1);
fprintf(' Approximation with tolerance = %f \n', tol);

Il codice scritto calcola la radice di una funzione $$ f $$ con la derivata $$ g $$ e il punto iniziale $$ x_0 $$ con una tolleranza $$ tol $$ e un limite di iterazioni $$ cap $$.

{: .prompt-info}

Esempio di utilizzo del codice:

f = @(x)(x+1)^2-9;
g = @(x)2*x + 2;
disp(newton(f, g , 3 ,10^-6 , 100));

{: .prompt-tip}

Dando come output:

Iter        x0
  1 	 2.125000 
  2 	 2.002500 
  3 	 2.000001 
  4 	 2.000000 

 x = 2.000000 produces f(x) = 0.000000 
 4 iterations
 Approximation with tolerance = 0.000001 
    2.0000

{: .prompt-tip}

Plot della funzione $$ f(x):= x*sin(x) $$

plot

Metodo delle secanti

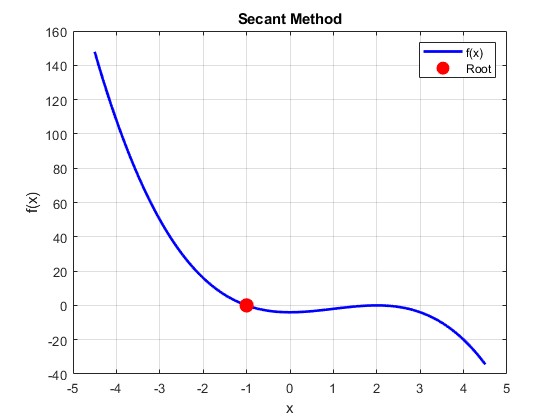
Il metodo delle secanti è un metodo iterativo per trovare gli zeri di una funzione.

Il metodo delle secanti è simile al metodo di Newton, ma invece di calcolare la derivata della funzione, approssima la derivata con una retta che passa per due punti.

Il metodo delle secanti può essere descritto come segue:

  1. Scegliere due punti iniziali $$ x_0 $$ e $$ x_1 $$
  2. Calcolare il punto in cui la retta che passa per $$ (x_0, f(x_0)) $$ e $$ (x_1, f(x_1)) $$ interseca l'asse x: $$ x_2 = x_1 - f(x_1) * \dfrac{(x_1 - x_0)}{(f(x_1) - f(x_0))} $$
  3. Ripetere i passaggi 2-3 fino a quando la differenza tra $$ x_n $$ e $$ x_{n-1} $$ è inferiore a una certa tolleranza stando attenti a non dividere per un valore troppo piccolo e a non superare un certo numero di iterazioni
function m = secant(f, x0, x1 , tol, cap)

i = 1;


dm = - f(x1)* (x1 - x0) / (f(x1) - f(x0));


disp('Iter x0 x1');
while abs(dm) > tol 

    if i > cap
        disp("iteration limit reached")
        m = "Error";
        return 
    end 
    
    m  = x1;
    x0 = x1;
    x1 = x1 + dm;
    fprintf("%i \t %f \t %f \n", i, x0 , x1)
    

    dm = - f(x1)* (x1 - x0) / (f(x1) - f(x0));
    i = i + 1;
end 

fprintf('\n x = %f produces f(x) = %f \n %i iterations\n', m, feval(f,m), i-1);
fprintf(' Approximation with tolerance = %f \n', tol);

Il codice calcola la radice di una funzione $$ f $$ con il punto iniziale $$ x_0 $$ e $$ x_1 $$ con una tolleranza $$ tol $$ e un limite di iterazioni $$ cap $$.

{: .prompt-info}

Esempio di utilizzo del codice:

f = @(x)(x+1)^2-9;
g = @(x)2*x + 2;
disp(secant(f,-3 , 3 ,10^-6 , 100));

{: .prompt-tip}

Dando come output:

example
Iter x0 x1
1 	 3.000000 	 -0.500000 
2 	 -0.500000 	 1.444444 
3 	 1.444444 	 2.471698 
4 	 2.471698 	 1.955705 
5 	 1.955705 	 1.996749 
6 	 1.996749 	 2.000024 
7 	 2.000024 	 2.000000 

 x = 2.000024 produces f(x) = 0.000145 
 7 iterations
 Approximation with tolerance = 0.000001 
    2.0000

{: .prompt-tip}

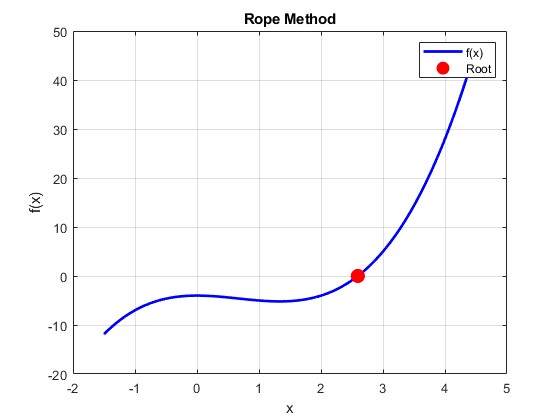
Plot della funzione $$ f(x):= -x^3 + 3x^2 - 4 $$

plot

Metodo delle corde

Il metodo delle corde è un metodo iterativo per trovare gli zeri di una funzione.

Il metodo delle corde è simile al metodo delle secanti, ma invece di calcolare il punto in cui la retta che passa per $$ (x_0, f(x_0)) $$ e $$ (x_1, f(x_1)) $$ interseca l'asse x, calcola il punto in cui la retta che passa per $$ (a, f(a)) $$ e $$ (b, f(b)) $$ interseca l'asse x.

Il metodo delle corde può essere descritto come segue:

  1. Scegliere due punti iniziali $$ a $$ e $$ b $$
  2. Calcolare il punto in cui la retta che passa per $$ (a, f(a)) $$ e $$ (b, f(b)) $$ interseca l'asse x: $$ x_2 = b - f(b) * \dfrac{(b - a)}{(f(b) - f(a))} $$
  3. Ripetere i passaggi 2-3 fino a quando la differenza tra $$ x_n $$ e $$ x_{n-1} $$ è inferiore a una certa tolleranza stando attenti a non dividere per un valore troppo piccolo e a non superare un certo numero di iterazioni
function m = rope(f, g, x0, tol, cap)

i = 1;
m = x0;

ca = g(m);
dm = - f(m) / ca;

disp('Iter x0');
while abs(dm) > tol 

    if i > cap
        disp("iteration limit reached")
        m = "Error";
        return 
    end 

    m  = m + dm;
    fprintf("%i \t %f \n", i, m)
    
    dm = - f(m) / ca;
    i = i + 1;
end 

fprintf('\n x = %f produces f(x) = %f \n %i iterations\n', m, feval(f,m), i-1);
fprintf(' Approximation with tolerance = %f \n', tol);

Il codice scritto calcola la radice di una funzione $$ f $$ con la derivata $$ g $$ e il punto iniziale $$ x_0 $$ con una tolleranza $$ tol $$ e un limite di iterazioni $$ cap $$.

{: .prompt-info}

Esempio di utilizzo del codice:

f = @(x)(x+1)^2-9;
g = @(x)2*x + 2;
disp(rope(f, g , 3 ,10^-6 , 100));

{: .prompt-tip}

Dando come output:

Iter        x0
1 	 2.125000 
2 	 2.029297 
3 	 2.007217 
4 	 2.001798 
5 	 2.000449 
6 	 2.000112 
7 	 2.000028 
8 	 2.000007 
9 	 2.000002 
10 	 2.000000 

 x = 2.000000 produces f(x) = 0.000003 
 10 iterations
 Approximation with tolerance = 0.000001 
    2.0000

{: .prompt-tip}

Plot della funzione $$ f(x):= x^3 - 2x^2 - 4 $$

plot

Matrici

$$ A \cdot x = b $$ Che belle le matrici, vero?

Fattorizzazione LU

La fattorizzazione LU è un metodo per fattorizzare una matrice $$ A $$ in due matrici una triangolare inferiore e un' altra triangolare inferiore $$L$$ower $$U$$pper.

La fattorizzazione LU può essere descritta come segue:

  1. Scegliere una matrice $$ A $$
  2. Verificare che la matrice sia quadrata
  3. calcoliamo la colonne di $$ L $$ e le righe di $$ U $$ con la seguente formula: $$ L(i, j) = \dfrac{U(i, j)}{U(j, j)} $$
  4. calcoliamo la matrice $$ U $$ con la seguente formula: $$ U(i, j:n) = U(i, j:n) - L(i, j) * U(j, j:n) $$
  5. passaggi 3-4 fino a quando la matrice è fattorizzata
  6. restituire le matrici $$ L $$ e $$ U $$
function [L, U] = LUfactorization(A)

    [n, m] = size(A);
    
    if n ~= m
        error('Matrix must be square');
    end

    L = eye(n); 
    U = A;

    for k = 1:n-1
        for i = k+1:n
            L(i, k) = U(i, k) / U(k, k);
            U(i, k:n) = U(i, k:n) - L(i, k) * U(k, k:n);
        end
    end
end

{: .prompt-info}

Esempio di utilizzo del codice:

A = [1 , 2, 3; 4, 5 ,6 ;7, 8, 11];
[L,U] = LUfactorization(A);

disp(L)
disp(U)

disp(L*U)

{: .prompt-tip}

Dando come output:

L =    |1     0     0|
       |4     1     0|
       |7     2     1|

U =    |1     2     3|
       |0    -3    -6|
       |0     0     2|

LU =   |1     2     3|
       |4     5     6|
       |7     8    11|

Fattorizzazione LU con pivoting parziale

La fattorizzazione LU con pivoting parziale è un metodo per fattorizzare una matrice in due matrici triangolari inferiori e superiori con pivoting parziale.

Il pivoting parziale è un metodo per scambiare le righe di una matrice in modo che il pivot sia il più grande possibile.

Il pivot deve essere il più grande possibile per evitare errori di arrotondamento.

La fattorizzazione LU con pivoting parziale può essere descritta come segue:

  1. Scegliere una matrice $$ A $$
  2. Verificare che la matrice sia quadrata
  3. Scegliere il pivot più grande nella colonna corrente
  4. Scambiare la riga corrente con la riga del pivot
  5. Calcoliamo la colonne di $$ L $$ e le righe di $$ U $$ con la seguente formula: $$ L(i, j) = \dfrac{U(i, j)}{U(j, j)} $$
  6. Calcoliamo la matrice $$ U $$ con la seguente formula: $$ U(i, j:n) = U(i, j:n) - L(i, j) * U(j, j:n) $$
  7. Passaggi 3-6 fino a quando la matrice è fattorizzata
  8. Restituire le matrici $$ L $$ e $$ U $$
  function [L, U, P] = LUfactorization_partial_pivoting(A)

    [m, n] = size(A);

    L = eye(m);
    U = A; 
    P = eye(m);


    for k = 1:min(m, n)

        [~, pivot] = max(abs(U(k:m, k)));
        pivot = pivot + k - 1;

        if pivot ~= k
            U([k, pivot], :) = U([pivot, k], :);
            P([k, pivot], :) = P([pivot, k], :);
            if k > 1
                L([k, pivot], 1:k-1) = L([pivot, k], 1:k-1);
            end
        end

        for i = k+1:m
            L(i, k) = U(i, k) / U(k, k);
            U(i, k:n) = U(i, k:n) - L(i, k) * U(k, k:n);
        end
    end

    if m > n
        U = U(1:n, :);
        L = L(:, 1:n);
    end
end

{: .prompt-info}

Esempio di utilizzo del codice:

A = [4, 3, 2;
     3, 2, 1;
     2, 1, 3;
     1, 4, 5];

[L, U, P] = LUfactorization_partial_pivoting(A);

disp('Matrix A:');
disp(A);
disp('Permutation matrix P:');
disp(P);
disp('Lower triangular matrix L:');
disp(L);
disp('Upper triangular matrix U:');
disp(U);

disp('Verification: P * A should be equal to L * U');
disp(P * A);
disp(L * U);

{: .prompt-tip}

Dando come output:

Matrix A:
     |4     3     2|
     |3     2     1|
     |2     1     3|
     |1     4     5|

Row permutation matrix P:
     |0     0     0     1|
     |1     0     0     0|
     |0     0     1     0|
     |0     1     0     0|

Column permutation matrix Q:
     |0     1     0|
     |0     0     1|
     |1     0     0|

Lower triangular matrix L:
    |1.0000         0         0|
    |0.4000    1.0000         0|
    |0.6000    0.3889    1.0000|
    |0.2000    0.7778   -0.0571|

Upper triangular matrix U:
    |5.0000    1.0000    4.0000|
    |     0    3.6000    1.4000|
    |     0         0   -1.9444|

Verification: P * A * Q should be equal to L * U
     |5     1     4|
     |2     4     3|
     |3     2     1|
     |1     3     2|

     |5     1     4|
     |2     4     3|
     |3     2     1|
     |1     3     2|

{: .prompt-info}

Un altro esempio di utilizzo del codice:

A = [1 , 2 , 3 , 4 ;
     5 , 6 , 7 , 8 ;
     9 , 10, 11, 12;]

[L, U, P] = LUfactorization_partial_pivoting(A);

disp('Matrix A:');
disp(A);
disp('Permutation matrix P:');
disp(P);
disp('Lower triangular matrix L:');
disp(L);
disp('Upper triangular matrix U:');
disp(U);

disp('Verification: P * A should be equal to L * U');
disp(P * A);
disp(L * U);

{: .prompt-tip}

Dando come output:

A =

     |1     2     3     4|
     |5     6     7     8|
     |9    10    11    12|

Matrix A:
     |1     2     3     4|
     |5     6     7     8|
     |9    10    11    12|

Permutation matrix P:
     |0     0     1|
     |1     0     0|
     |0     1     0|

Lower triangular matrix L:
    |1.0000         0         0|
    |0.1111    1.0000         0|
    |0.5556    0.5000    1.0000|

Upper triangular matrix U:
    |9.0000   10.0000   11.0000   12.0000|
    |     0    0.8889    1.7778    2.6667|
    |     0         0   -0.0000   -0.0000|

Verification: P * A should be equal to L * U
     |9    10    11    12|
     |1     2     3     4|
     |5     6     7     8|

     |9    10    11    12|
     |1     2     3     4|
     |5     6     7     8|

Fattorizzazione LU con pivoting totale

La fattorizzazione LU con pivoting totale è un metodo per fattorizzare una matrice in due matrici triangolari inferiori e superiori con pivoting totale.

Il pivoting totale è un metodo per scambiare le righe e le colonne di una matrice in modo che il pivot sia il più grande possibile.

Il pivot deve essere il più grande possibile per evitare errori di arrotondamento.

La fattorizzazione LU con pivoting totale può essere descritta come segue:

  1. Scegliere una matrice $$ A $$
  2. Verificare che la matrice sia quadrata
  3. Scegliere il pivot più grande nella matrice
  4. Scambiare la riga corrente con la riga del pivot
  5. Scambiare la colonna corrente con la colonna del pivot
  6. Calcoliamo la colonne di $$ L $$ e le righe di $$ U $$ con la seguente formula: $$ L(i, j) = \dfrac{U(i, j)}{U(j, j)} $$
  7. Calcoliamo la matrice $$ U $$ con la seguente formula: $$ U(i, j:n) = U(i, j:n) - L(i, j) * U(j, j:n) $$
  8. Passaggi 3-7 fino a quando la matrice è fattorizzata
  9. Restituire le matrici $$ L $$ e $$ U $$
function [L, U, P, Q] = LUfactorization_total_pivoting(A)

    [m, n] = size(A);


    L = eye(m);
    U = A;
    P = eye(m);
    Q = eye(n);


    for k = 1:min(m, n)
        [pivot_row, pivot_col] = find(abs(U(k:m, k:n)) == max(max(abs(U(k:m, k:n)))), 1);
        pivot_row = pivot_row + k - 1;
        pivot_col = pivot_col + k - 1;

        if pivot_row ~= k
            U([k, pivot_row], :) = U([pivot_row, k], :);
            P([k, pivot_row], :) = P([pivot_row, k], :);
            if k > 1
                L([k, pivot_row], 1:k-1) = L([pivot_row, k], 1:k-1);
            end
        end

        if pivot_col ~= k
            U(:, [k, pivot_col]) = U(:, [pivot_col, k]);
            Q(:, [k, pivot_col]) = Q(:, [pivot_col, k]);
        end

        for i = k+1:m
            L(i, k) = U(i, k) / U(k, k);
            U(i, k:n) = U(i, k:n) - L(i, k) * U(k, k:n);
        end
    end

    if m > n
        U = U(1:n, :);
        L = L(:, 1:n);
    end
end

{: .prompt-info}

Esempio di utilizzo del codice:

A = [4, 3, 2;
     3, 2, 1;
     2, 1, 3;
     1, 4, 5];

[L, U, P, Q] = LUfactorization_total_pivoting(A);

disp('Matrix A:');
disp(A);
disp('Row permutation matrix P:');
disp(P);
disp('Column permutation matrix Q:');
disp(Q);
disp('Lower triangular matrix L:');
disp(L);
disp('Upper triangular matrix U:');
disp(U);

disp('Verification: P * A * Q should be equal to L * U');
disp(P * A * Q);
disp(L * U);

{: .prompt-tip}

Dando come output:

Matrix A:
    |4     3     2|
    |3     2     1|
    |2     1     3|
    |1     4     5|

Row permutation matrix P:
    |0     0     0     1|
    |1     0     0     0|
    |0     0     1     0|
    |0     1     0     0|

Column permutation matrix Q:
    |0     1     0|
    |0     0     1|
    |1     0     0|

Lower triangular matrix L:
    |1.0000         0         0|
    |0.4000    1.0000         0|
    |0.6000    0.3889    1.0000|
    |0.2000    0.7778   -0.0571|

Upper triangular matrix U:
    |5.0000    1.0000    4.0000|
    |     0    3.6000    1.4000|
    |     0         0   -1.9444|

Verification: P * A * Q should be equal to L * U
    |5     1     4|
    |2     4     3|
    |3     2     1|
    |1     3     2|

    |5     1     4|
    |2     4     3|
    |3     2     1|
    |1     3     2|

{: .prompt-info}

Un altro esempio di utilizzo del codice:

A = [1 , 2 , 3 , 4 ;
     5 , 6 , 7 , 8 ;
     9 , 10, 11, 13;]

[L, U, P, Q] = LUfactorization_total_pivoting(A);


disp('Matrix A:');
disp(A);
disp('Row permutation matrix P:');
disp(P);
disp('Column permutation matrix Q:');
disp(Q);
disp('Lower triangular matrix L:');
disp(L);
disp('Upper triangular matrix U:');
disp(U);


disp('Verification: P * A * Q should be equal to L * U');
disp(P * A * Q);
disp(L * U);

{: .prompt-tip}

Dando come output:

A =

     |1     2     3     4|
     |5     6     7     8|
     |9    10    11    13|

Matrix A:
     |1     2     3     4|
     |5     6     7     8|
     |9    10    11    13|

Row permutation matrix P:
     |0     0     1|
     |1     0     0|
     |0     1     0|

Column permutation matrix Q:
     |0     1     0     0|
     |0     0     0     1|
     |0     0     1     0|
     |1     0     0     0|

Lower triangular matrix L:
    |1.0000         0         0|
    |0.3077    1.0000         0|
    |0.6154    0.3043    1.0000|

Upper triangular matrix U:
   |13.0000    9.0000   11.0000   10.0000|
   |      0   -1.7692   -0.3846   -1.0769|
   |      0         0    0.3478    0.1739|

Verification: P * A * Q should be equal to L * U
    |13     9    11    10|
    | 4     1     3     2|
    | 8     5     7     6|

    |13     9    11    10|
    | 4     1     3     2|
    | 8     5     7     6|

Risoluzione di sistemi lineari con sostituzione in avanti

La sostituzione in avanti è un metodo per risolvere un sistema lineare con una matrice triangolare inferiore.

La sostituzione in avanti può essere descritta come segue:

  1. Scegliere una matrice $$ L $$ e un vettore $$ b $$
  2. Calcolare il vettore $$ x $$ con la seguente formula: $$ x(1) = b(1) / L(1, 1) $$ $$ x(i) = (b(i) - \sum_{j=1}^{i-1} L(i, j) * x(j)) / L(i, i) $$
  3. Ripetere i passaggi 3-5 fino a quando il vettore $$ x $$ è calcolato
function x = forwardSubstitution(L, b)
    n = length(b);
    
    x = zeros(n, 1);

    for i = 1:n
        if L(i, i) == 0
            error('Matrix is singular!');
        end
        x(i) = (b(i) - L(i, 1:i-1) * x(1:i-1)) / L(i, i);
    end
end

{: .prompt-info}

Esempio di utilizzo del codice:

L = [1, 0, 0;
     2, 3, 0;
     4, 5, 6];

b = [3; 6; 24];

x = forwardSubstitution(L, b);

disp('Solution vector x:');
disp(x);

disp('Verification: L * x should be equal to b');
disp(L * x);
disp(b);

{: .prompt-tip}

Dando come output:

Solution vector 
x   =      [3]
           [0]
           [2]

Verification: L * x should be equal to b
b   =     [ 3]
          [ 6]
          [24]

L*x =     [ 3]
          [ 6]
          [24]

Risoluzione di sistemi lineari con sostituzione all'indietro

La sostituzione all'indietro è un metodo per risolvere un sistema lineare con una matrice triangolare superiore.

La sostituzione all'indietro può essere descritta come segue:

  1. Scegliere una matrice $$ U $$ e un vettore $$ b $$
  2. Calcolare il vettore $$ x $$ con la seguente formula:

$$ x(n) = b(n) / U(n, n) $$

$$ x(i) = (b(i) - \sum_{j=i+1}^{n} U(i, j) * x(j)) / U(i, i) $$

  1. Ripetere i passaggi 3-5 fino a quando il vettore $$ x $$ è calcolato
function x = backwardSubstitution(U, b)

    n = length(b);
    
    x = zeros(n, 1);
    
    for i = n:-1:1
        if U(i, i) == 0
            error('Matrix is singular!');
        end
        x(i) = (b(i) - U(i, i+1:n) * x(i+1:n)) / U(i, i);
    end
end

{: .prompt-info}

Esempio di utilizzo del codice:

U = [2, -1,  0;
     0,  3,  1;
     0,  0,  4];

b = [1; 8; 4];

x = backwardSubstitution(U, b);

disp('Solution vector x:');
disp(x);

disp('Verification: U * x should be equal to b');
disp(U * x);
disp(b);

{: .prompt-tip}

Dando come output:

Solution vector x:
x =  [1.6667]
     [2.3333]
     [1.0000]

Verification: U * x should be equal to b
b   =  [1]
       [8]
       [4]

U*x =  [1]
       [8]
       [4]

Interpolazione

Interpoliamo gente!

Metodo di interpolazione di Lagrange con la base di lagrange

Il metodo di interpolazione di Lagrange è un metodo per interpolare una funzione con un polinomio di grado n date n+1 coppie di punti.

Il metodo di interpolazione di Lagrange può essere descritto come segue:

  1. Scegliere n+1 coppie di punti $$ (x_0, y_0), (x_1, y_1), ..., (x_n, y_n) $$
  2. Calcolare il polinomio di interpolazione con la seguente formula: $$ P(x) = \sum_{i=0}^{n} y_i \prod_{j=0, j \neq i}^{n} \dfrac{x - x_j}{x_i - x_j} $$
function P = lagrangeInterpolation(x, y)

    n = length(x);


    P = zeros(1, n);

    for i = 1:n
        Li = 1;
        for j = 1:n
            if j ~= i
                Li = conv(Li, [1, -x(j)]) / (x(i) - x(j));
            end
        end

        P = P + y(i) * Li;
    end
end

{: .prompt-info}

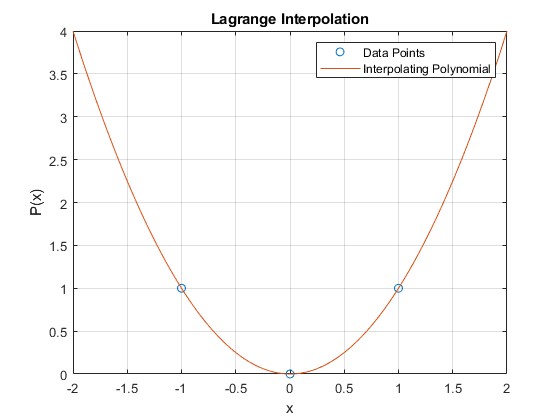
Esempio di utilizzo del codice:

x = [0, 1, -1];
y = [0, 1, 1];

P = lagrangeInterpolation(x, y);

disp('Coefficients of the interpolating polynomial:');
disp(P);

xi = linspace(-2, 2, 100);
yi = polyval(P, xi);  

figure;
plot(x, y, 'o', xi, yi, '-');
title('Lagrange Interpolation');
xlabel('x');
ylabel('P(x)');
legend('Data Points', 'Interpolating Polynomial');
grid on;

{: .prompt-tip}

Dando come output:

lagrange.png

Metodo di interpolazione di lagrange con i nodi di Chebyshev

Il metodo di interpolazione di Lagrange con i nodi di Chebyshev è un metodo per interpolare una funzione con un polinomio di grado n date n+1 coppie di punti.

Il metodo di interpolazione di Lagrange con i nodi di Chebyshev può essere descritto come segue:

  1. Scegliere n+1 coppie di punti $$ (x_0, y_0), (x_1, y_1), ..., (x_n, y_n) $$

  2. Calcolare i nodi di Chebyshev con la seguente formula:

    $$ x_i = \dfrac{1}{2} (b - a) \cos \left( \dfrac{2i - 1}{2n} \pi \right) + \dfrac{a + b}{2} $$

    $$ x_i = 1/2 * (b-a) * (x_i + 1) + a $$

  3. Calcolare il polinomio di interpolazione con la seguente formula: $$ P(x) = \sum_{i=0}^{n} y_i \prod_{j=0, j \neq i}^{n} \dfrac{x - x_j}{x_i - x_j} $$

function P = lagrangeChebyshevInterpolation(f, n, a, b)

    x = cos((2*(1:n) - 1) * pi / (2*n));
    x = 0.5 * (b - a) * (x + 1) + a; 

    y = f(x);

    P = zeros(1, n);
    for k = 1:n

        Lk = 1;
        for j = 1:n
            if j ~= k
                Lk = conv(Lk, [1, -x(j)]) / (x(k) - x(j));
            end
        end

        P = P + y(k) * Lk;
    end
end

{: .prompt-info}

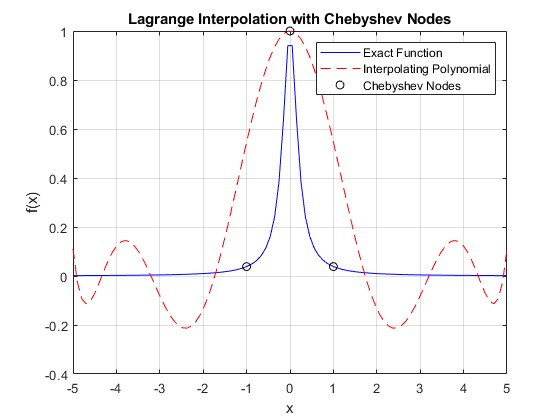
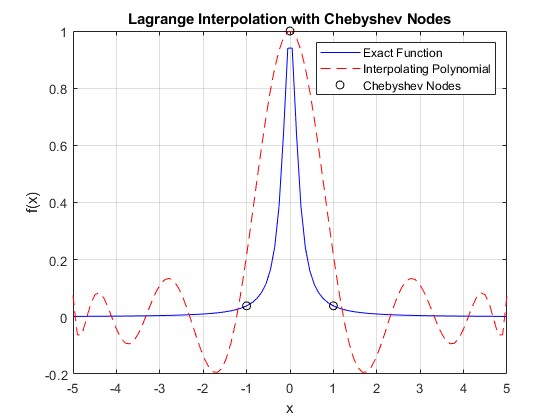
Esempio di utilizzo del codice:

f = @(x)(1./(1+25*x.^2));
n = 9;
a = -5;
b = 5;


P = lagrangeChebyshevInterpolation(f, n, a, b);


disp('Coefficients of the interpolating polynomial:');
disp(P);


xi = linspace(a, b, 100);
yi = polyval(P, xi); 
y_exact = f(xi);     

figure;
plot(xi, y_exact, 'b-', xi, yi, 'r--', x, f(x), 'ko');
title('Lagrange Interpolation with Chebyshev Nodes');
xlabel('x');
ylabel('f(x)');
legend('Exact Function', 'Interpolating Polynomial', 'Chebyshev Nodes');
grid on;

{: .prompt-tip}

Dando come output:

Per $$ n = 9 $$

lagrange_chebyshev.png

Per $$ n = 13 $$

lagrange_chebyshev.png

Eigenvectors ed Eigenvalues

Metodo delle potenze

Il metodo delle potenze è un metodo per calcolare l'autovalore dominante e l'autovettore associato di una matrice.

Il metodo delle potenze può essere descritto come segue:

  1. Scegliere una matrice $$ A $$ e un vettore $$ x_0 $$
  2. Calcolare il vettore $$ y = A * x_0 $$
  3. Calcolare il vettore $$ x_1 = \dfrac{y}{\lVert y \rVert _2} $$
  4. Ripetere i passaggi 2-3 fino a quando la differenza tra $$ x_n $$ e $$ x_{n-1} $$ è inferiore a una certa tolleranza
function [lambda, v] = method_of_powers(A, tol, max_iter)
    
    n = size(A, 1);
    v = ones(n, 1); 
    v = v / norm(v);

    lambda = 0;
    for k = 1:max_iter
 
        v_new = A * v; 
        lambda_new = max(abs(v_new)); 
        v_new = v_new / norm(v_new);

        if norm(v_new - v) < tol
            break;
        end

        v = v_new;
        lambda = lambda_new;
    end

    v = v_new;
end

{: .prompt-info}

Esempio di utilizzo del codice:

A = [4, 7; 2, 3];
tol = 1e-6;
max_iter = 1000;

[lambda, v] = method_of_powers(A, tol, max_iter);

disp('dominant eigenvalue:');
disp(lambda);

disp('dominant eigenvector:');
disp(v);

{: .prompt-tip}

Dando come output:

dominant eigenvalue:
    6.5894

dominant eigenvector:
    0.9058
    0.4238

Bonus

 /\_/\                             
( o.o )  Cosa ci sarai mai qui ?  
 > ^ <

Un algoritmo di cifratura che si basa su un sistema lineare

Questo algoritmo è stato un problema di una gara di logica-matematica, il problema era il seguente:

Dato l'algoritmo di cifratura $$ C $$ trovare la chiave $$ k $$ .

L'algoritmo di cifratura $$ C $$ è il seguente:

key = bytearray(b"???????????????")
message = bytearray(b"yellow submarine")

def get_bit(b, n):
    byte = b[n // 8]
    return (byte >> (7 - (n % 8))) & 1

def set_bit(b, n, v):
    byte = b[n // 8]
    byte &= ~(v << (7 - (n % 8)))
    byte |= v << (7 - (n % 8))
    b[n // 8] = byte
    return b

def bfri(i):
    a = hex(i)[2:]
    if (len(a) % 2 == 1):
        a = "0" + a
    return bytes.fromhex(a)

def xor(x1, x2):
    assert len(x1) == len(x2)
    return b"".join([bfri(x1[i] ^ x2[i]) for i in range(len(x1))])

def keysch(k):

    out = bytearray(b"\x00"*16)

    arr = [0 for i in range(128)]

    for i in range(128):
        for bit_loc in schedule[i]:
            arr[i] ^= get_bit(k, bit_loc)

    for i in range(128):
        out = set_bit(out, i, arr[i])
    
    return out

def enc(p, k):
    dat = bytearray(p)
    return xor(p, keysch(k))

def dec(c, k):
    dat = bytearray(c)
    return xor(c, keysch(k))

c = enc(message, key)

print("m:", message)
print("c:", c)

Una legenda per il codice :

  • la funzione $$ keysch $$ è la funzione che genera un array di 128 bit a partire da una chiave di 16 byte.

  • la funzione $$ enc $$ è la funzione che cifra un messaggio con una chiave.

  • la funzione $$ dec $$ è la funzione che decifra un messaggio con una chiave.

  • la funzione $$ xor $$ è la funzione che fa lo xor tra due byte.

  • la funzione $$ get_bit $$ è la funzione che prende un bit da un byte.

  • la funzione $$ set_bit $$ è la funzione che setta un bit in un byte.

  • la funzione $$ bfri $$ è la funzione che trasforma un intero in un byte.

  • la chiave $$ k $$ è una stringa di 16 byte.

  • il messaggio $$ m $$ è una stringa di 16 byte.

Ho portato questo problema come bonus, perchè racchiude molti aspetti dell'algebra lineare e di come possa essere utilizzata in contesti reali.

Il codice fornito è veramente lungo, ma è facile da capire una volta semplificato, qui riporto in breve cosa succede in questo algoritmo :

Visione generale

  1. il codice cifra un messaggio $$ m $$ con una sequenza pseudo-casuale di 128 bit generata da una chiave $$ k $$, chiamiamo questa sequenza $$ keyschedule $$
  2. la cifratura avviene con uno $$ xor $$ tra il messaggio e la keyschedule $$ c = m \oplus keyschedule $$
  3. la decifratura avviene con uno $$ xor $$ tra il messaggio cifrato e la keyschedule $$ m = c \oplus keyschedule $$

Il problema

Dobbiamo trovare la chiave $$ k $$ dato il messaggio cifrato $$ c $$ e il messaggio $$ m $$.

Riflessioni

Come ho detto prima, il problema fa parte di una competizione che si basava su problemi di crittografia è facile capire che se puoi ricavare la chiave da un algoritmo di cifratura, vuol dire che l'algoritmo è debole.

Dove sta la debolezza di questo algoritmo ?

in qualche modo la chiave $$ k $$ è collegata alla $$ keyschedule $$, quindi il problema si riduce a trovare la $$ keyschedule $$ e ricondurla alla chiave $$ k $$.

Partiamo da due osservazioni :

  1. possiamo ricavarci la $$keyschedule$$ dato il messaggio cifrato e il messaggio $$ keyschedule = m \oplus c $$
  2. adesso riflettiamo su cosa è la $$keyschedule$$ per trovare un collegamento con la chiave $$ k $$:
def keysch(k):

    out = bytearray(b"\x00"*16)

    arr = [0 for i in range(128)]

    for i in range(128):
        for bit_loc in schedule[i]:
            arr[i] ^= get_bit(k, bit_loc)

    for i in range(128):
        out = set_bit(out, i, arr[i])
    
    return out

Analisi

  • $$ schedule $$ è una tabella 128 x 128 dove ogni cella rappresenta una posizione da 0 a 127 .
  • la $$ keyschedule $$ è ricavata secondo la seguente regola :
    • per ogni riga della $$ schedule $$ prendiamo i bit della chiave $$ k $$ referenziati dalla riga e facciamo lo xor tra di loro.
    • il risultato di questo xor sarà il bit i della $$ keyschedule $$.

formalmente :

$$ keyschedule[i] = \bigoplus_{j \in schedule[i]} bit[j] $$

{: .prompt-tip }

ad esempio ho un byte 10010100 e schedule è [1, 3, 5, 7] allora il bit 0 della $$ keyschedule $$ sarà $$ bit[1] \oplus bit[3] \oplus bit[5] \oplus bit[7] $$

{: .prompt-info }

come facciamo a risalire alla chiave dalla $$ keyschedule $$ ?

La soluzione è molto semplice :

immaginiamo se accendessimo l'iesimo bit della chiave, questo influenzerà tutti i bit che sono referenziati nella $$ schedule $$.

Adesso ordiniamo i bit per colonne cosa otteniamo ?

Un sistema da 128 equazioni lineari con 128 incognite, le incognite sono i bit della chiave $$ k $$ e le equazioni ci dicono quante volte stiamo prendendo il bit i della chiave $$ k $$ nella $$ keyschedule $$.

{: .prompt-tip }

Risolvere questo sistema è molto semplice, pensiamo a cosa vuol dire fare lo xor tra due bit : $$ 0 \oplus 0 = 0 $$, $$ 1 \oplus 1 = 0 $$, $$ 0 \oplus 1 = 1 $$, $$ 1 \oplus 0 = 1 $$, quindi possiamo dire che fare lo xor tra due bit è come fare una somma in $Z/2Z$.

in maniera formale costruiamo il sistema lineare :

$$ system = \begin{bmatrix} bit_{1,1} & bit_{2,1} & \cdots & bit_{128,1} \\ bit_{1,2} & bit_{2,2} & \cdots & bit_{128,2} \\ \vdots & \vdots & \ddots & \vdots \\ bit_{1,128} & bit_{2,128} & \cdots & bit_{128,128} \\ \end{bmatrix} $$

dove $$ bit_{ij} $$ è il bit i della chiave k referenziato dalla j-esima riga della $$ schedule $$ $$ n $$ $$ mod 2 $$ volte.

la schedule non è altro che il vettore generato usando la matrice $$ system $$ sulla chiave $$ k $$ che è la nostra incognita

$$ \begin{equation} \begin{bmatrix} bit_{1,1} & bit_{2,1} & \cdots & bit_{128,1} \ bit_{1,2} & bit_{2,2} & \cdots & bit_{128,2} \ \vdots & \vdots & \ddots & \vdots \ bit_{1,128} & bit_{2,128} & \cdots & bit_{128,128} \end{bmatrix} \begin{bmatrix} x_1 \ x_2 \ \vdots \ x_{128} \end{bmatrix}

\begin{bmatrix} b_1 \ b_2 \ \vdots \ b_{128} \end{bmatrix} \end{equation} $$

Non ci resta che risolvere il sistema lineare per trovare la chiave $$ k $$ però c'è un problema, la matrice $$ system $$ è singolare quindi non possiamo risolvere il sistema lineare direttamente, ma ci troviamo in $Z/2Z$ quindi se due vettori sono linearmente dipendenti lo span del vettore dipendendente non è una retta ma $$ 1 $$ o $$ 0 $$ fantastico no? Quindi possiamo provare le due combinazioni ed ottenere la nostra key $$ k $$ .

Questo per far capire che lavorare su un campo finito è diverso da lavorare con $$ \mathbb{R} $$ se prendiamo un vettore e lo allunghiamo rapprentiamo una retta in $$ Z/2Z $$ invece giochiamo con dei punti. Usare diversi campi sulle matrici è un argomento molto interessante e che può essere sfruttato in molti contesti.

implementazione della soluzione

from sage.all_cmdline import *
from scheduu import schedule
from pwn import xor


def set_bit(b, n, v):
    byte = b[n // 8]
    byte &= ~(v << (7 - (n % 8)))
    byte |= v << (7 - (n % 8))
    b[n // 8] = byte
    return b

system = [[0 for i in range(128)] for i in range(128)]
pt = b'yellow submarine'
ct = b'\x83h\xdbWi\'\xc4\xf5\x02,_Z\x95p\xab\xc3'

keystream = xor(pt,ct)

for i in range(0,128):
    for k in schedule[i]:
        system[i][k]+=1
        system[i][k]%=2

b = []
for i in keystream:
    for j in range(8):
        b.append((i>>(7-j))&1)

A = matrix(GF(2),system)
b = vector(GF(2),b)
sol= A.solve_right(b)
key = bytearray(b"\x00" * 16)
ker = A.right_kernel()

for i in range(128):
    set_bit(key, i, int(sol[i]))
print(key)

_sol=sol+ker.basis()[0]
key_ = bytearray(b"\x00" * 16)
for i in range(128):
    set_bit(key_, i, int(_sol[i]))
print(key_)

Dando come output:

{: .prompt-tip }

sono_la_chiave!!

Potenza di matrici con gli eigenvectors

Gli autovalori possono essere sfruttati per calcolare la potenza di una matrice attraverso la diagonalizzazione. Questo metodo è particolarmente utile quando si ha a che fare con matrici che possono essere diagonalizzate, ossia quelle matrici che hanno una base di autovettori. Di seguito viene spiegato il processo in dettaglio.

Diagonalizzazione di una Matrice

Supponiamo di avere una matrice quadrata $$ A $$. Se $$ A $$ è diagonalizzabile, esistono una matrice diagonale $$ D $$ e una matrice invertibile $$ P $$ tali che:

$$ A = PDP^{-1} $$

Dove:

  • $$ D $$ è una matrice diagonale i cui elementi sulla diagonale principale sono gli autovalori di $$ A $$.
  • $$ P $$ è una matrice i cui colonne sono gli autovettori di $$ A $$.

Potenza di una Matrice

Se vogliamo calcolare $$ A^n $$ (dove $$ n $$ è un intero positivo), possiamo sfruttare la diagonalizzazione come segue:

  1. Diagonalizza $$ A $$: trova $$ P $$ e $$ D $$ tali che $$ A = PDP^{-1} $$.
  2. Eleva $$ A $$ alla potenza $$ n $$:

$$ A^n = (PDP^{-1})^n $$

  1. Utilizza la proprietà delle matrici diagonalizzate per semplificare il calcolo:

$$ A^n = (PDP^{-1})^n = PD^nP^{-1} $$

  1. Poiché $$ D $$ è diagonale, elevare $$ D $$ alla potenza $$ n $$ è semplice: basta elevare ciascun autovalore sulla diagonale alla potenza $$ n $$:

$$ D^n = \begin{pmatrix} \lambda_1^n & 0 & \cdots & 0 \\ 0 & \lambda_2^n & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_k^n \end{pmatrix} $$

Quindi, possiamo scrivere:

$$ A^n = P D^n P^{-1} $$

In questo modo, calcolare $$ A^n $$ diventa molto più semplice, poiché si riduce al calcolo delle potenze degli autovalori e alla moltiplicazione di matrici, anziché dover effettuare moltiplicazioni ripetute della matrice originale.

from sage.all_cmdline import *
from Crypto.Util.number import long_to_bytes,bytes_to_long

A = matrix(QQ, 2, [3, 1, 0, 2])

print(A)
print(A.eigenvectors_right())


P = matrix(QQ, 2, [1, 1, 0, -1])
D = matrix(QQ, 2, [3, 0, 0, 2])

print(D)

print(D ** 50)

D = D**50
print(P * D * P ** -1)

print(A ** 50)

assert (P * D * P ** -1 == A ** 50)

Esponenziazione veloce di una matrice

L'esponenziazione veloce di una matrice, anche conosciuta come "exponentiation by squaring", è un algoritmo efficiente per calcolare la potenza di una matrice in tempo logaritmico rispetto all'esponente. Questa tecnica è particolarmente utile quando si devono calcolare potenze elevate di una matrice, come ad esempio in applicazioni di algebra lineare, grafi, sistemi dinamici e crittografia.

Descrizione dell'Algoritmo

L'idea principale dell'esponenziazione veloce è ridurre il numero di moltiplicazioni matriciali sfruttando le proprietà delle potenze. L'algoritmo funziona in modo ricorsivo o iterativo dividendo l'esponente per 2.

Algoritmo Ricorsivo

Dato una matrice $$A$$ e un intero non negativo $$n$$, l'obiettivo è calcolare $$A^n$$:

  1. Se $$n = 0$$, allora $$A^0 = I$$ (la matrice identità).
  2. Se $$n = 1$$, allora $$A^1 = A$$.
  3. Se $$n$$ è pari, allora $$A^n = (A^{n/2})^2$$.
  4. Se $$n$$ è dispari, allora $$A^n = A \cdot A^{n-1}$$.

Algoritmo Iterativo

Un modo iterativo per eseguire l'esponenziazione veloce di una matrice è il seguente:

  1. Inizializzare il risultato $$R$$ come la matrice identità $$I$$.
  2. Utilizzare una variabile $$B$$ inizializzata a $$A$$ e una variabile $$n$$ per l'esponente.
  3. Ripetere i seguenti passaggi finché $$n &gt; 0$$:
  • Se $$n$$ è dispari, aggiornare $$R$$ come $$R = R \cdot B$$.
  • Aggiornare $$B$$ come $$B = B \cdot B$$.
  • Dividere $$n$$ per 2 (trascurando il resto).

Pseudocodice dell'Algoritmo Iterativo

Ecco uno pseudocodice dell'algoritmo iterativo:

  function B = fast_exp(A,k)
    B = eye(size(A));
    while k > 0
        if mod(k, 2) == 1
            B = B * A;
        end
        A = A * A;
        k = floor(k / 2);
    end

Esempio di Esponenziazione Veloce di una Matrice

{: .prompt-info}

Ecco un esempio di come utilizzare l'esponenziazione veloce per calcolare la potenza di una matrice:

A = eye(3);
A(1,2) = 1;

A = A*2;

disp(fast_exp(A,3));

{: .prompt-tip}

Dando come output:

     8    24     0
     0     8     0
     0     0     8

Complessità dell'Algoritmo

La complessità temporale dell'esponenziazione veloce di una matrice è $$O(\log n)$$ moltiplicazioni matriciali, dove $$n$$ è l'esponente. Ogni moltiplicazione di matrici di dimensione $$m \times m$$ ha una complessità di $$O(m^3)$$ utilizzando l'algoritmo standard, o può essere ridotta utilizzando algoritmi più avanzati come quello di Strassen.