- Date: April 2018
- Status: Deprecated
For language design, see Swift Differentiable Programming Design Overview.
Automatic Differentiation (AD), also known as algorithmic differentiation, is a family of techniques used to obtain the derivative of a function. Functions can be represented as a composition of elementary operators whose derivatives are well-known. While partial derivatives can be computed through different techniques, the most common is a recursive application of the chain rule in the reverse direction, called reverse-mode AD. Reverse-mode AD computes vector-Jacobian products, i.e. partial derivatives with respect to each input parameter, and it has become a prerequisite for implementing gradient-based learning methods. AD has a rich background, here are some great introductions: Introduction to Automatic Differentiation and Automatic Differentiation in Machine Learning: a Survey.
Most AD implementations work on a graph representation of a functional tensor program, and many have limited expressivity and extensibility. Frameworks based on a define-by-run programming model (to support dynamic computation graphs) often lack the ability to perform full-program static analysis and optimizations, and make it hard to diagnose errors and target hardware accelerators ahead of time.
The Swift for TensorFlow project aims to provide best-in-class support for AD - including the best optimizations, best error messages in failure cases, and the most flexibility and expressivity. To achieve this, we built support for AD right into the Swift compiler. Additionally, since AD is important to the broader scientific and numerical computing communities, we decided to build AD as a generic feature that is completely orthogonal to the TensorFlow support - the TensorFlow Swift library computes gradients using the AD features of the Swift language itself.
Automatic differentiation has been a research topic in scientific computing and HPC for nearly half a century. Traditional tools such as OpenAD, TAPENADE and ADIFOR are tools that transform existing source code. There are many advanced techniques that improved the performance of derivatives written in FORTRAN, but these tools have not gained wide adoption in the machine learning community. More recent AD systems like Stalin∇ (pronounced Stalingrad, available in Scheme), DiffSharp (available in F#), and ad (available in Haskell) achieved good usability by integrating the differential operator into the language, and are equipped with a complete set of AD features (such as forward/reverse, nested AD, Hessians, Jacobians, directional derivatives and checkpointing). They combine AD closely with functional programming languages.
Researchers in the deep learning community have built many library implementations of AD in Python and C++, including Autograd, TensorFlow, Pytorch, etc. Some of these libraries are implemented as a transformation on a standalone DSL (a graph) with a closed set of operators. Others are implemented using operator overloading directly on a subset of the source language. Although these libraries have gained wide adoption, the ones that leverage ahead-of-time AD do not expose an easy-to-use programming model, and the ones that have a friendlier programming model lack static analysis to perform more optimized AD.
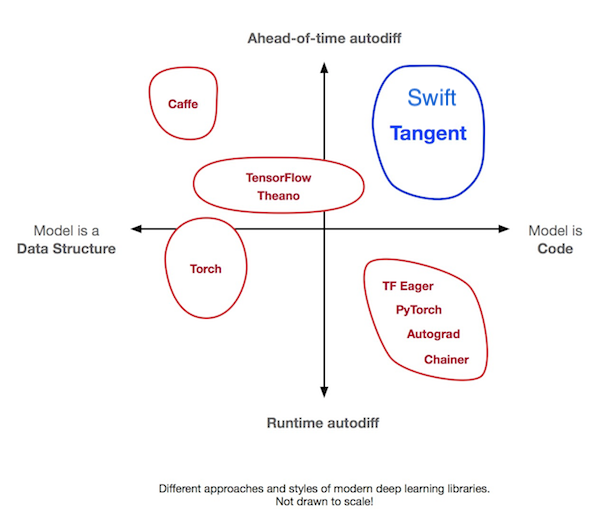
Two recent projects (Tangent and Myia) based their AD upon source code transformation (SCT), a technique that was common in advanced AD systems before the deep learning era such as Stalin∇. Both tools parse a Python subset into ASTs and transform a function to its derivatives either in AST or in a functional IR. These two projects fall into a category in deep learning tools that was previously underexplored: ahead-of-time differentiation + "model as code", as shown in the following diagram (cite: Tangent). While these tools are pushing the boundaries of Python, other research projects like DLVM experimented with SCT AD directly on a compiler IR that's analogous to the Swift Intermediate Language (SIL).
The horizontal axis of this diagram may remind people of the trade-offs between eager execution and graph building: In eager execution, the model is a subset of user code. In graph mode, the model is a data structure representing some code in a mini-language. The Graph Program Extraction technique combines the best of both worlds by reducing graphs to an implementation detail managed by the compiler. The vertical axis in the diagram adds a second dimension, Automatic Differentiation, where Swift achieves exactly the same by making AD a core feature of the language and the compiler.
There are two main approaches to automatic differentiation: recording program execution at runtime and static analysis over the program ahead of time - the primary difference is interpretation vs. compilation. The define-then-run approaches are usually implemented as a computation graph transformation that is analogous to the source code transformation (SCT) technique in the AD literature, and the define-by-run approaches are usually implemented with operator overloading (OO).
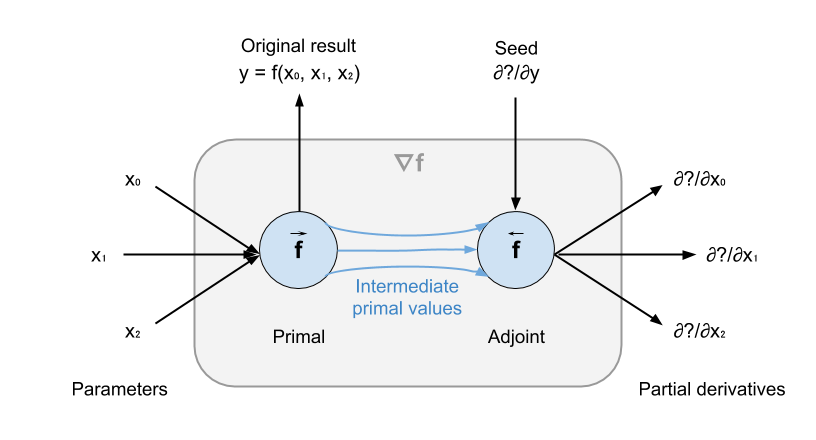
Given function f : (T0, T1, ..., Tn) -> U, reverse-mode AD turns f into a
function that computes the partial derivatives with respect to each parameter.
As illustrated below, the new function has two parts: a primal f_prim and an
adjoint f_adj. f_prim computes the original result, while storing primal
intermediate values for f_adj to reuse. f_adj computes the partial
derivatives of f with respect to the parameters.
The data structure used to store these values is called tape, also known as Wengert list. It is a data structure consisting of a trace of the program along with intermediate values. Each right-hand side of an assignment is a primitive operation that has a corresponding derivative. In compiler terms, Wengert lists are a fully-unrolled static single assignment (SSA) form. During execution of the primal, intermediate values generated by the primal that will be used in the adjoint computation are written to the tape. When control flow is involved, branch conditions and loop counters are pushed to the tape as well.
In f_adj, the derivatives of each operation in f_prim is then called, and
intermediate values are read from the tape in reverse order. When the
accumulation of partial derivatives reaches the parameters, we have obtained the
partial derivatives with respect to the parameters. These values are sometimes
also called the sensitivities of f.
Note that f_adj has an additional parameter: the seed. A differentiation seed
represents the back-propagated partial derivative. For example, if f is called
by g and we want to differentiate g to get ∇g = ∂g/∂(x0, x1, x2), then
g's corresponding adjoint g_adj will pass ∂g/∂y as the seed to f_adj, so
that f_adj will produce ∇g. When we want to compute ∇f = ∂f/∂(x0, x1, x2),
we simply pass in ∂y/∂y, i.e. 1, as the seed.
In this section, we dive deep into the syntax extensions and AD-specific APIs that allow users to define, use, and customize AD. To do this, we start with the type system.
We want our AD system to be fully extensible to the point where users can request the derivatives of a function taking their own user-defined numeric types, and even use this feature to implement data structure-dependent algorithms such as tree-recursive neural networks. Therefore, the Swift compiler makes no assumptions about individual math functions or the types it should support. We enable library designers and developers to easily define any type to represent a real vector space or declare functions as being differentiable, all in pure Swift code.
To achieve this, Swift’s AD system needs to know some key ingredients for a type to be compatible with differentiation, including:
-
The type must represent an arbitrarily ranked vector space (where tensors live). Elements of this vector space must be floating point numeric. There is an associated scalar type that is also floating point numeric.
-
How to initialize an adjoint value for a parameter from a scalar, with the same dimensionality as this parameter. This will be used to initialize a zero derivative when the parameter does not contribute to the output.
-
How to initialize a seed value from a value of the scalar type. This will be used to initialize a differentiation seed - usually
1.0, which representsdy/dy. Note: the seed type in the adjoint can be anOptional, so when there is no back-propagated adjoint, the value will be set tonil. However this will cause performance issues with TensorFlow’sTensortype today (optional checks causing send/receive). We need to finish the implementation of constant expression analysis to be able to fold away the optional check. -
How values of this type will combine at data flow fan-ins in the adjoint computation. By the sum and product rule, this is usually addition. Addition is defined on the
Numericprotocol.
Floating point scalars already have properties above, because of the conformance
to the FloatingPoint protocol, which inherits from the Numeric protocol.
Similarly, we define a VectorNumeric protocol, which declares the four
requirements to represent a vector space.
public protocol VectorNumeric {
associatedtype ScalarElement
associatedtype Dimensionality
init(_ scalar: ScalarElement)
init(dimensionality: Dimensionality, repeating repeatedValue: ScalarElement)
func + (lhs: Self, rhs: Self) -> Self
func - (lhs: Self, rhs: Self) -> Self
func * (lhs: Self, rhs: Self) -> Self
}VectorNumeric and Numeric/FloatingPoint are semantically disjoint. We say
that a type supports scalar differentiation when it conforms to
FloatingPoint. We say that a type supports vector differentiation when it
conforms to VectorNumeric while its ScalarElement supports scalar
differentiation (i.e. conforms to the FloatingPoint protocol).
Note: According to the standard library, Numeric is only suitable for
scalars, not for aggregate mathematical objects like vectors, and so is
FloatingPoint. Today we make VectorNumeric have duplicate operators, but we
hope to make a case for a more general numeric protocol in the Swift standard
library.
To make a type support differentiation, the user can simply add a conformance to
FloatingPoint or VectorNumeric. For example, TensorFlow’s Tensor<Scalar>
type supports differentiation by conditionally conforming to the VectorNumeric
protocol when the associated type Scalar conforms to FloatingPoint.
extension Tensor : VectorNumeric where Scalar : Numeric {
typealias Dimensionality = [Int32] // This is shape.
typealias ScalarElement = Scalar
init(_ scalar: ScalarElement) {
self = Raw.const(scalar)
}
init(dimensionality: [Int32], repeating repeatedValue: ScalarElement) {
self = Raw.fill(dims: Tensor(dimensionality), repeatedValue)
}
func + (lhs: Tensor, rhs: Tensor) -> Tensor { ... }
func - (lhs: Tensor, rhs: Tensor) -> Tensor { ... }
func * (lhs: Tensor, rhs: Tensor) -> Tensor { ... }
}Since VectorNumeric is general enough to provide all necessary ingredients for
differentiation and the compiler doesn’t make special assumptions about
well-known types, users can make any type support automatic differentiation. The
following example shows a generic tree structure Tree<Value>, written as an
algebraic data type, conditionally conforming to VectorNumeric by recursively
defining operations using pattern matching. Now, functions over Tree<Value>
can be differentiated!
indirect enum Tree<Value> {
case leaf(Value)
case node(Tree, Value, Tree)
}
extension Tree : VectorNumeric where Value : VectorNumeric {
typealias ScalarElement = Value.ScalarElement
typealias Dimensionality = Value.Dimensionality
init(_ scalar: ScalarElement) {
self = .leaf(Value(scalar))
}
init(dimensionality: Dimensionality, repeating repeatedValue: ScalarElement) {
self = .leaf(Value(dimensionality: dimensionality, repeating: repeatedValue))
}
static func + (lhs: Tree, rhs: Tree) -> Tree {
switch (lhs, rhs) {
case let (.leaf(x), .leaf(y)):
return .leaf(x + y)
case let (.leaf(x), .node(l, y, r)):
return .node(l, x + y, r)
case let (.node(l, x, r), .leaf(y)):
return .node(l, x + y, r)
case let (.node(l0, x, r0), .node(l1, y, r1)):
return .node(l0 + l0, x + y, r0 + r1)
}
}
static func - (lhs: Tree, rhs: Tree) -> Tree { ... }
static func * (lhs: Tree, rhs: Tree) -> Tree { ... }
static func / (lhs: Tree, rhs: Tree) -> Tree { ... }
}Once we have types that support differentiation, we can then define arbitrary functions over these types. Because we are aiming for an open and extensible system, we made the compiler agnostic of the actual operations - it does not have special knowledge of numeric standard library functions or distinguish between primitive operators and other functions. We recursively determine a function's differentiability based on:
- its type signature: whether inputs and the output support scalar differentiation or vector differentiation
- its visibility: if the function body is not visible by the Swift compiler (e.g. a C function or an argument which is a closure), then it is not differentiable
- its data flow: whether all instructions and function calls are differentiable along the data flow to be differentiated
Since the rule is recursively defined, it needs a base case, so that the
compiler will stop looking into function calls and determine the
differentiability. Functions representing such base cases are often referred to
in AD as "primitives". For that, we introduce the @differentiable attribute.
Users can use @differentiable to give any function guaranteed
differentiability. The attribute has a few associated arguments:
- the differentiation mode (currently only
reverseis supported) - the primal (optional, and should be specified if the adjoint requires checkpoints)
- the adjoint
For example, one can define the derivative of tanh and make the AD system
treat it as a "primitive", which is a base case when determining
differentiability.
// Differentiable with respect to all parameters using reverse-mode AD.
// The corresponding adjoint is `dTanh`.
@differentiable(reverse, adjoint: dTanh)
func tanh(_ x: Float) -> Float {
... some super low-level assembly tanh implementation ...
}
// d/dx tanh(x) = 1 - (tanh(x))^2
//
// Here, y is the original result of tanh(x), and x is the input parameter of the
// original function. We don't need to use `x` in tanh's adjoint because we already
// have access to the original result.
func dTanh(x: Float, y: Float, seed: Float) -> Float {
return (1.0 - y * y) * seed
}As the user would expect, in order to exclude functions that have parameters
that cannot be differentiated with respect to, @differentiable can explicitly
set parameters using withRespectTo:. Also, self can be set as a
differentiation parameter, because self may be a numeric type - math
operations in both the Swift standard library and the TensorFlow library are
defined as instance methods, e.g. FloatingPoint.squareRoot() and
Tensor.convolved(withFilter:strides:padding:).
extension Tensor {
// Differentiable with respect to `self` (the input) and the first parameter
// (the filter) using reverse-mode AD. The corresponding adjoint is `dConv`.
@differentiable(reverse, withRespectTo: (self, .0), adjoint: dConv)
func convolved(withFilter k: Tensor, strides: [Int32], padding: Padding) -> Tensor {
return #tfop("Conv2D", ...)
}
func dConv(k: Tensor, strides: [Int32], padding: Padding,
y: Tensor, seed: Tensor) -> Tensor {
...
}
}We currently support two differential operators: #gradient() and
#valueAndGradient(). The former takes a function and returns a function
that computes partial derivatives. The latter takes a function and returns a
function that computes both the original value and the vector-Jacobian products.
A trivial example is shown as follows:
@differentiable(reverse, adjoint: dTanh)
func tanh(_ x: Float) -> Float {
... some super low-level assembly tanh implementation ...
}
func dTanh(x: Float, y: Float, seed: Float) -> Float {
return (1.0 - (y * y)) * seed
}
func foo(_ x: Float, _ y: Float) -> Float {
return tanh(x) + tanh(y)
}
// Get the gradient function of tanh.
let dtanh_dx = #gradient(tanh)
dtanh_dx(2)
// Get the gradient function of foo with respect to the first parameter.
let dfoo_dx = #gradient(foo, withRespectTo: .0)
dfoo_dx(3, 4)Note that implementation of #gradient(foo, withRespectTo: .0) is still in progress.
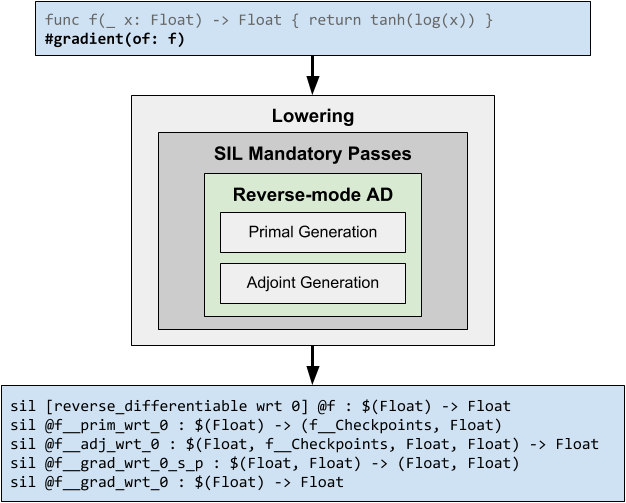
Automatic differentiation in Swift is a compiler transform implemented as a static analysis. AD benefits from being implemented on a functional IR like SSA form, so our implementation is a transformation on the Swift Intermediate Language. The differentiation pass is part of the mandatory lowering pass pipeline, and is run before Graph Program Extraction.
When differentiating a function in reverse mode, the compiler produces separate functions that contain the corresponding "primal code" and "adjoint code", which in turn compute the vector-Jacobian products of the computation.
When the #gradient() operator is applied on a function f : (T0, T1, ..., Tn) -> U, the compiler checks whether a @differentiable attribute exists on
this function. If it does, then the compiler generates a direct call to this
declared adjoint, passing in the original input parameters, the original result
and the seed. Otherwise, the compiler digs into the function and tries to
differentiate instructions and function calls within it. In this process, the
compiler generates:
- A struct type
C_f, whose members include primal intermediate values as stored properties and strongly-typed tapes (only if there's any control flow or loops). We call this struct "checkpoints" for implementation modeling purposes. - A primal function
f_prim : (T0, T1, ..., Tn) -> (C_f, U)that returns primal checkpoints and the original result. - An adjoint function
f_adj : (T0, T1, ..., Tn, C_f, U, U) -> (T0, T1, ..., Tn)that takes primal checkpoints, the original result, and a seed and returns the vector-Jacobian products. - A "canonical gradient" (a seedable, result-preserving differentiated function)
f_can_grad : (T0, T1, ..., Tn, U) -> (U, T0, T1, ..., Tn)which internally callsf_primand uses the primal's returns to callf_adj. The last parameter of this function takes a differentiation seed. This function returns the original result and the vector-Jacobian products. - A finalized gradient function
∇f : (T0, T1, ..., Tn) -> (T0, T1, ..., Tn)which internally callsf_can_gradusing a default seed1and throws away the first result (the first result would be used if#valueAndGradient()was the differential operator).
More than one function exists to wrap the canonical gradient function
f_can_grad, because we'll support a variety of AD configurations, e.g.
#gradient() and #valueAndGradient(). We expect the finalized gradient
function ∇f to be inlined and have other normal optimization passes applied,
to expose primal-adjoint data flow and eliminate dead code.
AD in Swift involves changes to the syntax, the type checker, the standard
library, the SIL instruction set, the compiler pass pipeline, and even the
runtime (for tape operations). The detailed implementation is out of scope for
this whitepaper. As an overview, currently we have the infrastructure and the
overall workflow implemented, but code synthesis within primal generation and
adjoint generation, including control flow graph canonicalization, loop counter
insertion and tape management, are still a work in progress. This means that
today's differential operators work only when there's a @differentiable
attribute specifying the adjoint (or both the primal and the adjoint).
Completing the AD implementation is our immediate priority.
AD is an unconventional feature in a general-purpose programming language like
Swift. In order to allow users to specify what formal parameter to differentiate
with respect to and make it work well with the type checker, we use the
#-literal syntax that takes parameter indices or self, and which is parsed
into a distinct expression in the Swift AST. However, we would prefer to define
differential operators as regular generic functions.
As described in the document, we initially provide two differential operators on
functions: #gradient and #valueAndGradient. Differentiating functions,
however, do not provide a similar developer experience as
let y = log(x)
#gradient(y, wrt: x)... in which #gradient is effectively a flow-sensitive differential operator.
However, from a technical standpoint, function-to-function transformation that
we initially develop is the foundation even for flow-sensitive differentiation.
Once the foundation is done, syntactic features on top such as this one will be
considered and implemented to enable more expressive user code.
When defining a custom adjoint for a function, today we use the attribute
@differentiable(reverse, adjoint: someAdjointFunction) where
someAdjointFunction is defined out-of-line. However, there are a few problems:
- adjoints are never directly called by the user, so it does not make sense to require the user to define such a function with a standalone function name,
- out-of-line definition of adjoints also makes it hard for user to customize
checkpointing in the original computation, and 3)
@differentiableuses confusing indices to refer to parameters to differentiate with respect to. To address these issues, a possible solution would be to introduce an inline syntax with keywordsadjointandwrt:
func foo(_ a: Float, _ b: String) -> Float {
let x = ... a ...
let y = ...
return y
adjoint let seed wrt a, b { // `seed` is the backpropagated value.
return ... x ... * seed
// ^
// The primal value `x` falls out of lexical scoping, and will be checkpointed.
}
}Statically differentiating a function requires the body of the function to be
visible to the compiler. However, this limits the expressiveness of differential
operators. For example, users can't apply #gradient to a function argument
that has a function type because the compiler can't always see into the body of
the original function.
func foo(_ f: (Float) -> Float) -> Float {
return #gradient(f)(0)
}test.swift:2:22: error: cannot differentiate an opaque closure
return #gradient(f)(0)
~~~~~~~~~~^~
test.swift:1:12: note: value defined here
func foo(_ f: (Float) -> Float) -> Float {
^~~~~~~~~~~~~~~~~~~One potential solution is to introduce a new function calling convention
@convention(differentiable), which causes function references to carry their
primal and adjoint function pointers with them. This enables the compiler to
directly call the primal and the adjoint, without the need to see into the
function declaration.
Real-world models are often written as a struct type that declares parameters,
but differentiation parameters in the #gradient expression syntax currently
only support parameter indices or self. When the prediction function is
defined as an instance method on the type, how can we express "differentiate
prediction(for:) with respect to all parameters"?
One possibility is to leverage program synthesis to generate an aggregate type
representing all parameters in a model type, and make the differential operator
#gradient return such an aggregate value. We have begun experimenting with
this approach but need to develop the ideas further.
Some machine learning models require manipulating the gradient with respect to
certain values, e.g. gradient clipping. Tangent
provides such a feature as a syntax extension in Python. We are interested in
figuring out the best programming model to express derivative surgery, for example:
introducing a compiler-known replaceGradient(of:_:) API.
func prediction(for input: Tensor<Float>, parameters: Tensor<Float>) -> Float {
var prediction = input
for _ in 0...5 {
// Gradient clipping.
replaceGradient(of: prediction) { dPred in
max(min(dPred, 1), -1)
}
prediction = lstm.prediction(for: input, parameters)
}
return prediction
}One commonly requested feature for ML training is the ability to trade off computation for lower memory consumption, since the backward pass preserves checkpoints from the primal computation to prevent recomputation in the adjoint computation. Selectively discarding and rematerializing primal values is a common technique called checkpointing. There have been decades of research contributions such as binomial checkpointing. We would like to incorporate these techniques directly into our model.
Perturbation confusion and sensitivity confusion are two common bugs in nested uses of the differential operator using SCT techniques, and require user attention to correctly resolve. The application of rank-2 polymorphism in the ad package in Haskell defined away sensitivity confusion, but Swift’s type system does not support that today. In order to support higher-order differentiation with sound semantics and predictable behavior in Swift, we need to teach the compiler to carefully emit diagnostics and reject malformed cases.
Our existing AD infrastructure has pre-allocated space for forward-mode AD, e.g.
the first parameter to the @differentiable attribute. Although it's not a
commonly requested feature, it will enable efficient computation of
Hessian-vector products for research in optimization methods. It is also easier
to implement than reverse-mode AD and may enable further engineering
explorations in mixing forward and reverse.