Skip to content

Latest commit

 

History

History
369 lines (317 loc) · 9.01 KB

README.md

File metadata and controls

369 lines (317 loc) · 9.01 KB
Raw

1038. 把二叉搜索树转换为累加树

English Version

题目描述

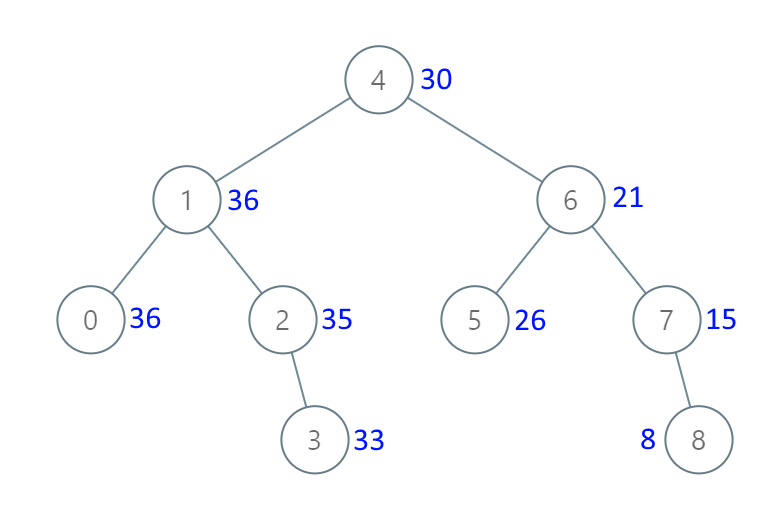
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键 小于 节点键的节点。
  • 节点的右子树仅包含键 大于 节点键的节点。
  • 左右子树也必须是二叉搜索树。

注意：该题目与 538: https://leetcode-cn.com/problems/convert-bst-to-greater-tree/  相同

 

示例 1：

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

 

提示：

  • 树中的节点数介于 1 和 100 之间。
  • 每个节点的值介于 0 和 100 之间。
  • 树中的所有值 互不相同 。
  • 给定的树为二叉搜索树。

解法

二叉搜索树的中序遍历（左根右）结果是一个单调递增的有序序列，我们反序进行中序遍历（右根左），即可以得到一个单调递减的有序序列。通过累加单调递减的有序序列，我们可以得到大于等于 node.val 的新值，并重新赋值给 node。

关于反序中序遍历，有三种方法，一是递归遍历，二是栈实现非递归遍历，三是 Morris 遍历。

Python3

递归遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    add = 0

    def bstToGst(self, root: TreeNode) -> TreeNode:
        if root:
            self.bstToGst(root.right)
            root.val += self.add
            self.add = root.val
            self.bstToGst(root.left)
        return root

Morris 遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def bstToGst(self, root: TreeNode) -> TreeNode:
        s = 0
        node = root
        while root:
            if root.right is None:
                s += root.val
                root.val = s
                root = root.left
            else:
                next = root.right
                while next.left and next.left != root:
                    next = next.left
                if next.left is None:
                    next.left = root
                    root = root.right
                else:
                    s += root.val
                    root.val = s
                    next.left = None
                    root = root.left
        return node

Java

递归遍历：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int add = 0;
    public TreeNode bstToGst(TreeNode root) {
        if (root != null) {
            bstToGst(root.right);
            root.val += add;
            add = root.val;
            bstToGst(root.left);
        }
        return root;
    }
}

Morris 遍历：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode bstToGst(TreeNode root) {
        int s = 0;
        TreeNode node = root;
        while (root != null) {
            if (root.right == null) {
                s += root.val;
                root.val = s;
                root = root.left;
            } else {
                TreeNode next = root.right;
                while (next.left != null && next.left != root) {
                    next = next.left;
                }
                if (next.left == null) {
                    next.left = root;
                    root = root.right;
                } else {
                    s += root.val;
                    root.val = s;
                    next.left = null;
                    root = root.left;
                }
            }
        }
        return node;
    }
}

C++

递归遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int add = 0;
    TreeNode* bstToGst(TreeNode* root) {
        if (root) {
            bstToGst(root->right);
            root->val += add;
            add = root->val;
            bstToGst(root->left);
        }
        return root;
    }
};

Morris 遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* bstToGst(TreeNode* root) {
        int s = 0;
        TreeNode* node = root;
        while (root)
        {
            if (root->right == nullptr) {
                s += root->val;
                root->val = s;
                root = root->left;
            }
            else
            {
                TreeNode* next = root->right;
                while (next->left && next->left != root)
                {
                    next = next->left;
                }
                if (next->left == nullptr)
                {
                    next->left = root;
                    root = root->right;
                }
                else
                {
                    s += root->val;
                    root->val = s;
                    next->left = nullptr;
                    root = root->left;
                }
            }
        }
        return node;
    }
};

递归遍历：

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func bstToGst(root *TreeNode) *TreeNode {
	add := 0
	var dfs func(*TreeNode)
	dfs = func(node *TreeNode) {
		if node != nil {
			dfs(node.Right)
			node.Val += add
			add = node.Val
			dfs(node.Left)
		}
	}
	dfs(root)
	return root
}

Morris 遍历：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func bstToGst(root *TreeNode) *TreeNode {
	s := 0
	node := root
	for root != nil {
		if root.Right == nil {
			s += root.Val
			root.Val = s
			root = root.Left
		} else {
			next := root.Right
			for next.Left != nil && next.Left != root {
				next = next.Left
			}
			if next.Left == nil {
				next.Left = root
				root = root.Right
			} else {
				s += root.Val
				root.Val = s
				next.Left = nil
				root = root.Left
			}
		}
	}
	return node
}

...