class: middle, center, title-slide
Lecture 5: Probabilistic reasoning
Prof. Gilles Louppe
[email protected]
- Bayesian networks
- Semantics
- Construction
- Independence relations
- Inference
- Parameter learning
.footnote[Credits: CS188, UC Berkeley.]
class: middle
class: middle
The explicit representation of the joint probability distribution grows exponentially with the number of variables.
Independence and conditional independence assumptions reduce the number of probabilities that need to be specified. They can be represented explicitly in the form of a Bayesian network.
.grid[ .kol-3-4[
A Bayesian network is a .bold[directed acyclic graph] where
- each node corresponds to a random variable;
- observed or unobserved
- discrete or continuous
- each edge is directed and indicates a direct probabilistic dependency between two variables;
- each node
$X_i$ is annotated with a conditional probability distribution$${\bf P}(X_i | \text{parents}(X_i))$$ that defines the distribution of$X_i$ given its parents in the network.
???
In the simplest case, conditional distributions are represented as conditional probability tables (CPTs).
class: middle
- Variables:
$\text{Burglar}$ ,$\text{Earthquake}$ ,$\text{Alarm}$ ,$\text{JohnCalls}$ ,$\text{MaryCalls}$ . - The network topology can be defined from domain knowledge:
- A burglar can set the alarm off
- An earthquake can set the alaram off
- The alarm can cause Mary to call
- The alarm can cause John to call
.footnote[Credits: CS188, UC Berkeley.]
???
I am at work, neighbor John calls to say my alarm is ringing, but neighbor Mary does not call. Sometimes it's set off by minor earthquakes. Is there a burglar?
class: middle
???
Blackboard: example of calculation, as in the next slide.
A Bayesian network implicitly encodes the full joint distribution as a product of local distributions, that is
Proof:
- By the chain rule,
$P(x_1, ..., x_n) = \prod_{i=1}^n P(x_i | x_1, ..., x_{i-1})$ . - Provided that we assume conditional independence of
$X_i$ with its predecessors in the ordering given the parents, and provided$\text{parents}(X_i) \subseteq \{ X_1, ..., X_{i-1}\}$ , we have$$P(x_i | x_1, ..., x_{i-1}) = P(x_i | \text{parents}(X_i)).$$ - Therefore,
$P(x_1, ..., x_n) = \prod_{i=1}^n P(x_i | \text{parents}(X_i))$ .
class: middle
class: middle
.grid[
.kol-1-2[.width-90[ ]]
.kol-1-2[.width-100[
]]
.kol-1-2[.width-100[]]
]
The dentist's scenario can be modeled as a Bayesian network with four variables, as shown on the right.
By construction, the topology of the network encodes conditional independence assertions. Each variable is independent of its non-descendants given its parents:
-
$\text{Weather}$ is independent of the other variables. -
$\text{Toothache}$ and$\text{Catch}$ are conditionally independent given$\text{Cavity}$ .
.footnote[Credits: CS188, UC Berkeley.]
???
A dentist is examining a patient's teeth. The patient has a cavity, but the dentist does not know this. However, the patient has a toothache, which the dentist observes.
class: middle
.grid.center[
.kol-1-3[.width-70[ ]]
.kol-2-3[.width-80[
]]
.kol-2-3[.width-80[ ]
]
]
]
Edges may correspond to causal relations.
.grid.center[
.kol-1-5[.width-60[ ]]
.kol-2-5[
]]
.kol-2-5[
|
| ] | ||
| ] |
.footnote[Credits: CS188, UC Berkeley.]
???
Causal model
class: middle
... but edges need not be causal!
.grid.center[
.kol-1-5[.width-60[ ]]
.kol-2-5[
]]
.kol-2-5[
|
| ] | ||
| ] |
.footnote[Credits: CS188, UC Berkeley.]
???
Diagnostic model
Bayesian networks can be constructed in any order, provided that the conditional independence assertions are respected.
- Choose some ordering of the variables
$X_1, ..., X_n$ . - For
$i=1$ to$n$ :- Add
$X_i$ to the network. - Select a minimal set of parents from
$X_1, ..., X_{i-1}$ such that$P(x_i | x_1, ..., x_{i-1}) = P(x_i | \text{parents}(X_i))$ . - For each parent, insert a link from the parent to
$X_i$ . - Write down the CPT.
- Add
class: middle
.question[Do these networks represent the same distribution? Are they as compact?]
???
For the left network:
- P (J|M ) = P (J)? No
- P (A|J, M ) = P (A|J)? P (A|J, M ) = P (A)? No
- P (B|A, J, M ) = P (B|A)? Yes
- P (B|A, J, M ) = P (B)? No
- P (E|B, A, J, M ) = P (E|A)? No
- P (E|B, A, J, M ) = P (E|A, B)? Yes
Since the topology of a Bayesian network encodes conditional independence assertions, it can be used to answer questions about the independence of variables given some evidence.
.center[Example: Are
class: middle
.grid[
.kol-1-2[
Is
Counter-example:
- Low pressure causes rain causes traffic, high pressure causes no rain causes no traffic.
- In numbers:
.footnote[Credits: CS188, UC Berkeley.]
class: middle
.grid[
.kol-1-2[
Is
We say that the evidence along the cascade blocks the influence.
]
.kol-1-2.center[.width-100[ ]
]
.footnote[Credits: CS188, UC Berkeley.]
class: middle
.grid[ .kol-1-2[
Is
Counter-example:
- Project due causes both forums busy and lab full.
- In numbers:
.footnote[Credits: CS188, UC Berkeley.]
class: middle
.grid[
.kol-1-2[
Is
Observing the parent blocks the influence between the children.
]
.kol-1-2.center[.width-80[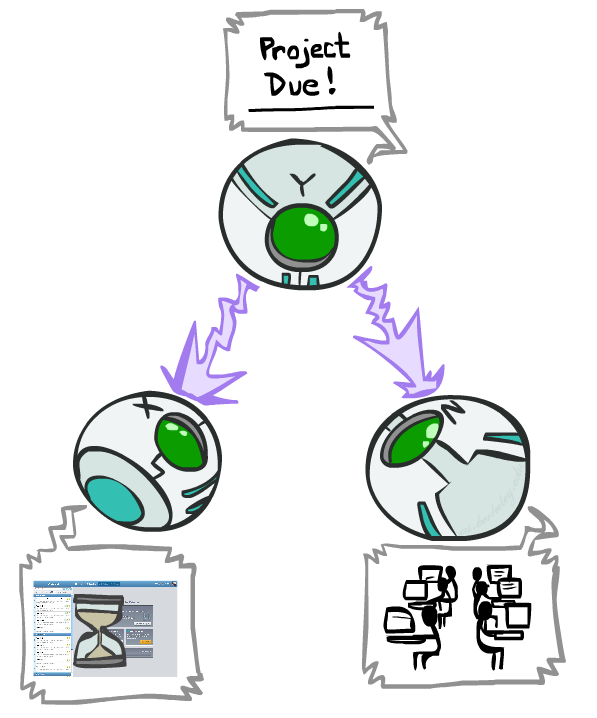 ]
]
.footnote[Credits: CS188, UC Berkeley.]
class: middle
.grid[ .kol-1-2[
Are
- The ballgame and the rain cause traffic, but they are not correlated.
- (Prove it!)
Are
- Seeing traffic puts the rain and the ballgame in competition as explanation.
- This is backwards from the previous cases. Observing a child node activates influence between parents.
]
.kol-1-2.center[.width-80[
 ]
]
.footnote[Credits: CS188, UC Berkeley.]
???
Proof:
and
therefore
class: middle
Let us assume a complete Bayesian network.
Are
Consider all (undirected) paths from
- If one or more active path, then independence is not guaranteed.
- Otherwise (i.e., all paths are inactive), then independence is guaranteed.
class: middle
.grid[ .kol-2-3[
A path is active if each triple along the path is active:
- Cascade
$A \to B \to C$ where$B$ is unobserved (either direction). - Common parent
$A \leftarrow B \rightarrow C$ where$B$ is unobserved. - v-structure
$A \rightarrow B \leftarrow C$ where$B$ or one of its descendents is observed.
.footnote[Credits: CS188, UC Berkeley.]
class: middle
.grid[ .kol-1-2[
-
$L \perp T' | T$ ? -
$L \perp B$ ? -
$L \perp B|T$ ? -
$L \perp B|T'$ ? -
$L \perp B|T, R$ ?
]
.kol-1-2.width-80.center[ ]
]
]
]
???
- Yes
- Yes
- (maybe)
- (maybe)
- Yes
exclude: true class: middle
A node
exclude: true class: middle
A node
class: middle
class: middle
Inference is concerned with the problem .bold[computing a marginal and/or a conditional probability distribution] from a joint probability distribution:
.grid[ .kol-1-3.center[Simple queries:] .kol-2-3[${\bf P}(X_i|e)$] ] .grid[ .kol-1-3.center[Conjunctive queries:] .kol-2-3[${\bf P}(X_i,X_j|e)={\bf P}(X_i|e){\bf P}(X_j|X_i,e)$] ] .grid[ .kol-1-3.center[Most likely explanation:] .kol-2-3[$\arg \max_q P(q|e)$] ] .grid[ .kol-1-3.center[Optimal decisions:] .kol-2-3[$\arg \max\_a \mathbb{E}_{p(s'|s,a)} \left[ V(s') \right]$] ]
.footnote[Credits: CS188, UC Berkeley.]
???
Explain what
Insist on the importance of inference. Inference <=> reasoning.
Start from the joint distribution
- Select the entries consistent with the evidence
$E_1, ..., E_k = e_1, ..., e_k$ . - Marginalize out the hidden variables to obtain the joint of the query and the evidence variables:
$${\bf P}(Q,e_1,...,e_k) = \sum_{h_1, ..., h_r} {\bf P}(Q, h_1, ..., h_r, e_1, ..., e_k).$$ - Normalize:
$$\begin{aligned} Z &= \sum_q P(q,e_1,...,e_k) \\\\ {\bf P}(Q|e_1, ..., e_k) &= \frac{1}{Z} {\bf P}(Q,e_1,...,e_k) \end{aligned}$$
class: middle
Consider the alarm network and the query
???
&\propto P(B) \sum_e P(e) \sum_a P(a|B,e)P(j|a)P(m|a)
class: middle
Inference by enumeration is slow because the whole joint distribution is joined up before summing out the hidden variables.
.footnote[Credits: CS188, UC Berkeley.]
class: middle
Factors that do not depend on the variables in the summations can be factored out, which means that marginalization does not necessarily have to be done at the end, hence saving some computations.
For the alarm network, we have $$\begin{aligned} {\bf P}(B|j,m) &\propto \sum_e \sum_a {\bf P}(B)P(e){\bf P}(a|B,e)P(j|a)P(m|a) \\ &= {\bf P}(B) \sum_e P(e) \sum_a {\bf P}(a|B,e)P(j|a)P(m|a). \end{aligned}$$
class: middle
Same complexity as DFS:
???
-
$n$ is the number of variables. -
$d$ is the size of their domain.
class: middle
Despite the factoring, inference by enumeration is still inefficient. There are repeated computations!
- e.g.,
$P(j|a)P(m|a)$ is computed twice, once for$e$ and once for$\lnot e$ . - These can be avoided by storing intermediate results.
???
Inefficient because the product is evaluated left-to-right, in a DFS manner.
The .bold[Variable Elimination] algorithm carries out summations right-to-left and stores intermediate factors to avoid recomputations. The algorithm interleaves:
- Joining sub-tables
- Eliminating hidden variables
.center.width-80[]
.footnote[Credits: CS188, UC Berkeley.]
class: middle
Query:
- Start with the initial factors (the local CPTs, instantiated by the evidence).
- While there are still hidden variables:
- Pick a hidden variable
$H$ - Join all factors mentioning
$H$ - Eliminate H
- Pick a hidden variable
- Join all remaining factors
- Normalize
class: middle
- Each factor
$\mathbf{f}_i$ is a multi-dimensional array indexed by the values of its argument variables. E.g.: .grid[ .kol-1-2[ $$ \begin{aligned} \mathbf{f}_4 &= \mathbf{f}_4(A) = \left(\begin{matrix} P(j|a) \\ P(j|\lnot a) \end{matrix}\right) = \left(\begin{matrix} 0.90 \\ 0.05 \end{matrix}\right) \\ \mathbf{f}_4(a) &= 0.90 \\ \mathbf{f}_4(\lnot a) &= 0.5 \end{aligned}$$ ] ] - Factors are initialized with the CPTs annotating the nodes of the Bayesian network, conditioned on the evidence.
class: middle
The pointwise product
- Exactly like a database join!
- The variables of
$\mathbf{f}_3$ are the union of the variables in$\mathbf{f}_1$ and$\mathbf{f}_2$ . - The elements of
$\mathbf{f}_3$ are given by the product of the corresponding elements in$\mathbf{f}_1$ and$\mathbf{f}_2$ .
class: middle
Summing out, or eliminating, a variable from a factor is done by adding up the sub-arrays formed by fixing the variable to each of its values in turn.
For example, to sum out
class: middle
.question[Run the variable elimination algorithm for the query
class: middle
Consider the query
-
$\sum_m P(m|a) = 1$ , therefore$M$ is irrelevant for the query. - In other words,
${\bf P}(J|b)$ remains unchanged if we remove$M$ from the network.
.italic[Theorem.]
class: middle
Consider the query
Work through the two elimination orderings:
$Z, X_1, ..., X_{n-1}$ $X_1, ..., X_{n-1}, Z$
What is the size of the maximum factor generated for each of the orderings?
- Answer:
$2^{n+1}$ vs.$2^2$ (assuming boolean values)
class: middle
The computational and space complexity of variable elimination is determined by the largest factor.
- The elimination ordering can greatly affect the size of the largest factor.
- The optimal ordering is NP-hard to find. There is no known polynomial-time algorithm to find it.
Exact inference is intractable for most probabilistic models of practical interest. (e.g., involving many variables, continuous and discrete, undirected cycles, etc).
We must resort to approximate inference algorithms:
- Sampling methods: produce answers by repeatedly generating random numbers from a distribution of interest.
- Variational methods: formulate inference as an optimization problem.
- Belief propagation methods: formulate inference as a message-passing algorithm.
- Machine learning methods: learn an approximation of the target distribution from training examples.
class: middle
class: middle
When modeling a domain, we can choose a probabilistic model specified as a Bayesian network. However, specifying the individual probability values is often difficult.
A workaround is to use a parameterized family
???
Connect back to the Kolmogorov axioms: we have upgraded
class: middle
Suppose we have a set of
The likelihood of the parameters
The maximum likelihood estimate (MLE)
class: middle
In practice,
- Write down the log-likelihood
$L(\theta) = \log P({\bf d}|\theta)$ of the parameters$\theta$ . - Write down the derivative
$\frac{\partial L}{\partial \theta}$ of the log-likelihood of the parameters$\theta$ . - Find the parameter values
$\theta^*$ such that the derivatives are zero (and check whether the Hessian is negative definite).
???
Note that:
- evaluating the likelihood may require summing over hidden variables, i.e., inference.
- finding
$\theta^*$ may be hard; modern optimization techniques help.
class: middle
What is the fraction
Suppose we unwrap
class: middle
Red and green wrappers depend probabilistically on flavor. E.g., the likelihood for a cherry candy in green wrapper is $$\begin{aligned} &P(\text{cherry}, \text{green}|\theta,\theta_1, \theta_2) \\ &= P(\text{cherry}|\theta,\theta_1, \theta_2) P(\text{green}|\text{cherry}, \theta,\theta_1, \theta_2) \\ &= \theta (1-\theta_1). \end{aligned}$$
The likelihood for the parameters, given
class: middle
The derivatives of
???
Again, results coincide with intuition.
class: middle
.question[In case (a), if we unwrap 1 candy and get 1 cherry, what is the MLE? How confident are we in this estimate?]
- With small datasets, maximum likelihood estimation can lead to overfitting.
- The MLE does not provide a measure of uncertainty about the parameters.
We can treat parameter learning as a .bold[Bayesian inference] problem:
- Make the parameters
$\theta$ random variables and treat them as hidden variables. - Specify a prior distribution
${\bf P}(\theta)$ over the parameters. - Then, as data arrives, update our beliefs about the parameters to obtain the posterior distribution
${\bf P}(\theta|\mathbf{d})$ .
.question[How should Figure 20.2 (a) be updated?]
class: middle
What is the fraction
We assume a Beta prior
Then, observing a cherry candy yields the posterior $$\begin{aligned} P(\theta|\text{cherry}) &\propto P(\text{cherry}|\theta) P(\theta) \\ &= \theta \text{Beta}(\theta|a,b) \\ &= \theta (1-\theta)^{b-1} \theta^{a-1} (1-\theta)^{b-1} \\ &= \theta^a (1-\theta)^{b-1} \\ &= \text{Beta}(\theta|a+1,b). \end{aligned}$$
class: middle
class: middle
When the posterior cannot be computed analytically, we can use maximum a posteriori (MAP) estimation, which consists in approximating the posterior with the point estimate
class: middle, center
(Step-by-step code example)
- A Bayesian Network specifies a full joint distribution. BNs are often exponentially smaller than an explicitly enumerated joint distribution.
- The topology of a Bayesian network encodes conditional independence assumptions between random variables.
- Inference is the problem of computing a marginal and/or a conditional probability distribution from a joint probability distribution.
- Exact inference is possible for simple Bayesian networks, but is intractable for most probabilistic models of practical interest.
- Approximate inference algorithms are used in practice.
- Parameters of a Bayesian network can be learned from data using maximum likelihood estimation or Bayesian inference.
class: end-slide, center count: false
The end.












