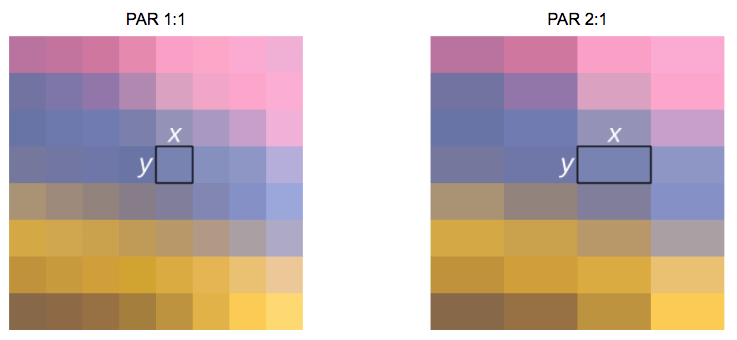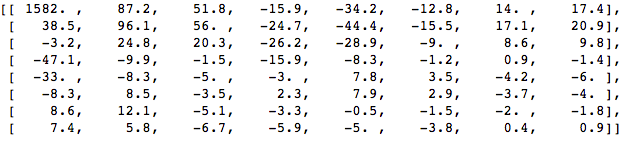Skip to content

Latest commit

 

History

History
930 lines (606 loc) · 64.9 KB

README-ko.md

File metadata and controls

930 lines (606 loc) · 64.9 KB
Raw

license

Intro

비디오 기술에 대한 친절한 소개 자료입니다. 비록 소프트웨어 개발자/엔지니어를 대상으로 작성 했지만, 누구나 배울 수 있는 글이 되었으면 합니다. 아이디어는 비디오 기술 뉴비를 위한 미니 워크샵에서 비롯되었습니다.

가능한 쉬운 단어, 많은 시각 자료 그리고 실용적인 예제들로 디지털 비디오의 컨셉을 소개하며 어디서든 사용할 수 있는 지식이 될 수 있는 것이 목표입니다. 언제나 수정 사항, 제안 등을 보내셔서 개선해주세요.

실습 섹션에서는 도커가 필요하며 이 레포지토리를 클론하셔야 합니다.

git clone https://github.com/leandromoreira/digital_video_introduction.git
cd digital_video_introduction
./setup.sh

알림: ./s/ffmpeg나 ./s/mediainfo 명령을 사용하는 경우,필요로 하는 모든 요구사항이 포함된 도커 앱을 실행하는 것을 의미합니다.

All the hands-on should be performed from the folder you cloned this repository. For the jupyter examples you must start the server ./s/start_jupyter.sh and copy the URL and use it in your browser.

모든 실습 내용은 여러분이 클론한 레포지토리 폴더에서 실행되어야 합니다.
주피터 예제의 경우, ./s/start_jupyter.sh로 서버를 반드시 실행해야하며 URL을 복사해 브라우저에서 사용하시면 됩니다.

변경로그

  • DRM 시스템이 추가되었습니다.
  • 1.0.0 버전이 릴리즈 되었습니다.
  • 요약 버전의 중국어 번역이 추가되었습니다.

색인

기초 용어

이미지는 2차원 매트릭스로 생각할 수 있습니다. 여기에 색상을 고려한다면, 색상 데이터 제공에 사용되는 추가적인 차원이 있는 3차원 매트릭스로 여길 수 있습니다.

삼원색(빨간색, 초록색, 파란색)을 사용해 색상들을 표현하는 경우, 빨간색, 초록색, 파란색 순의 세 가지 평면을 정의할 수 있습니다.

an image is a 3d matrix RGB

이 매트릭스의 각각의 점을 픽셀(화소)라 부를 것입니다. 하나의 픽셀은 주어진 색상의 강도(보통 숫자 값)를 표현합니다. 예를들어, 빨간 픽셀은 초록생이 0, 파란색이 0이고 빨간색이 최대인 것을 의미하지요. 핑크 색상 픽셀은 세 가지 색상의 조합으로 구성되어 있습니다. 대표적인 0부터 255까지의 숫자 범위를 사용하면 핑크색 픽셀은 빨간색=255, 초록색=192, 파란색=203으로 정의됩니다.

색상 이미지를 인코딩하는 또 다른 방법

이미지를 구성하는 색상들을 표현하는데에는 다양한 모델들이 존재합니다. 예를들면 RGB 모델을 사용할 때 3바이트를 사용하는 것 대신, 각 픽셀을 표현하는데 한 바이트만 필요한 인덱스 팔레트를 사용할 수 있지요. 이러한 모델에서는 3차원 매트릭스 대신 2차원 매트릭스를 사용하여 색상을 표현할 수 있으며, 메모리를 아낄 수 있지만 색상에 대한 몇 가지 옵션들을 포기해야하죠.

NES palette

예를들어 아래의 사진을 한 번 보세요. 첫 번째 얼굴은 모든 색상이 표현되어있지요. 다른 것들은 빨간색, 초록색, 파란색 평면입니다. (회색 톤으로 나옴)

RGB channels intensity

여기서 빨간색(두 번째 얼굴의 밝은 부분들)이 색상에 많이 나타나는 것을 볼 수 있습니다. 반면 파란색(마지막 얼굴)은 대부분 마리오의 눈과 옷의 일부에만 나타납니다. 모든 색상의 영향력이 낮은 부분은 마리오의 수염(가장 어두운 부분)입니다.

각각의 색상 강도는 특정한 양의 비트를 필요로 합니다. 여기서 양이란 비트 깊이 입니다. 각 색상 평면당 8비트(0부터 255 사이의 값을 가지는)를 할애했다고 가정하면 24비트의 색 깊이(8 비트 * R/G/B의 3가지 평면)를 가지게 되며, 2의 24승 가지의 서로 다른 색상을 사용할 수 있음을 의미합니다.

세상에서 비트로 이미지가 캡쳐되는 원리에 대해 배울 수 있는 훌륭한 글 입니다.

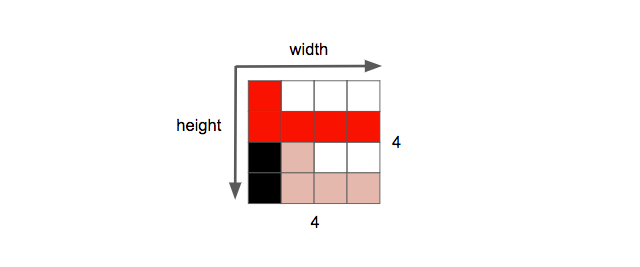
이미지의 또 다른 속성은 해상도입니다. 해상도는 차원 하나에 포함될 수 있는 픽셀의 수를 의미합니다. 이는 보통 width x height로 표현됩니다. 그 예로 아래에는 4x4 이미지가 있습니다.

image resolution

실습: 이미지와 색상 가지고 놀기

주피터를 사용하여 이미지와 색 가지고 놀기를 해볼 수 있어요.

이미지 필터(외곽선 검출, 강조, 블러)에 대해 학습할 수 있습니다.

이미지나 비디오를 다루다보면 볼 수 있는 또 다른 속성인 **종횡비(aspect ratio)**가 있습니다. 이는 이미지나 픽셀의 폭과 높이의 비례 관계를 간단하게 표현하는 방법입니다.

사람들이 이 영상 혹은 사진은 16x9야라고 한다면 이는 일반적으로 화면 종횡비(DAR) 에 대한 이야기를 하는 것입니다. 반면에 각각의 픽셀의 서로 다른 형태에 대한 것은 픽셀 종횡비(PAR) 라고 부릅니다.

display aspect ratio

pixel aspect ratio

DVD는 DAR 4:3이다.

DVD의 실제 해상도는 704x480이지만 10:11(704x10/480x11)의 PAR로 인해 4:3의 종횡비를 유지합니다.

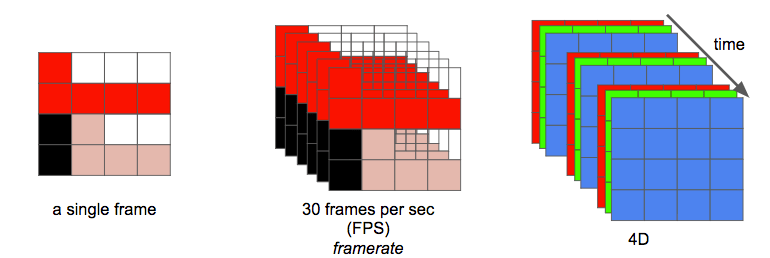
마지막으로 비디오는 또다른 차원으로 볼 수 있는 시간의 축에 나열된 n개의 프레임의 연속으로 정의할 수 있습니다.
여기서 n은 프레임레이트 혹은 초당 프레임 수 입니다.

video

비디오의 비트 레이트는 동영상을 표시하는데 초당 필요한 비트의 수입니다.

비트레이트 = 폭 * 높이 * 비트 깊이 * 초당 프레임 수

예를들어 어떤 영상이 30fps, 24비트 픽셀 깊이, 480x240의 해상도에 압축을 하지 않은 경우라면 초당 82,944,000비트 혹은 82.944 Mbps (30x480x240x24)가 필요로 합니다.

비트 레이트가 거의 일정한 경우 이를 고정 비트레이트(CBR)라고 부르며 가변의 경우에는 가변 비트레이트(VBR)라 부릅니다.

이 그래프는 프레임이 검은색인 동안에는 그리 많은 비트를 소비하지 않는 제한된 VBR을 보여줍니다.

constrained vbr

초기에는 엔지니어들이 여분의 대역폭 소모 없이 두 배의 인지 가능한 프레임 레이트로 비디오를 표시하는 기술을 개발했습니다. 이 기술은 인터레이싱 비디오라고 부릅니다. 이는 1프레임에서 화면의 절반을 보내고 나머지 절반을 그 다음 프레임에 보냅니다.

오늘날의 화면은 대부분 프로그레시브 스캔 기술을 사용합니다. 프로그레시브는 각 프레임의 모든 라인을 순서대로 그리는 영상을 출력, 저장, 전송하는 기술입니다.

interlaced vs progressive

이제 어떻게 이미지가 디지털로 표현되는지, 색상이 어떻게 배치되어 영상 표현에 어느 정도의 초당 비트 수가 필요한지, 그게 고정(CBR)인지 가변(VBR)인지에 대한 것과 해상도와 프레임 레이트와 인터레이스드, PAR와 같은 많은 용어들을 배웠습니다.

연습: 비디오 속성 확인

ffmpeg이나 mediainfo로 속성 살펴보기

중복 제거

압축 없이는 비디오를 사용할 수 없다는 것을 배웠습니다. 30fps인 720p 해상도의 한 시간 짜리 영상은 278GB*를 필요로합니다. DEFLATE(PKZIP, Gzip, PNG에 사용되는)와 같은 무손실 데이터 압축 알고리즘을 사용하는 경우 대역폭을 충분히 줄일 수 없으므로 비디오를 압축할 다른 방법을 찾아야합니다.

* 1280 x 720 x 24 x 30 x 3600 (폭, 높이, 픽셀 당 비트 수, fps, 영상 시간)

이를 위해서는, 우리의 눈을 속여야합니다. 눈은 색상보다 명암 구분을 더 잘합니다. 영상은 변화가 거의 없는 많은 이미지들로 이루어져있으며, 각 프레임들은 같거나 유사한 색상을 사용하는 많은 영역들이 포함되어 있습니다.

색상, 휘도, 시각

시각은 색상보다 명암에 더 민감하며, 이를 테스트 해볼 수 있습니다. 이 사진을 보세요.

luminance vs color

만일 왼쪽의 이미지에서 사각형 A와 B가 동일한 색상이라는 사실을 눈치채지 못하셨다면 정상입니다. 우리의 뇌는 색상보다는 명암에 더 신경쓰도록 만들기 때문이지요. 오른쪽의 사진에서는 같은 색상을 연결해주는 커넥터가 있기 때문에 우리의 뇌는 두 사각형이 동일한 색상이라는 사실을 쉽게 파악할 수 있습니다.

시각은 어떻게 동작하는가에 대한 간단한 설명

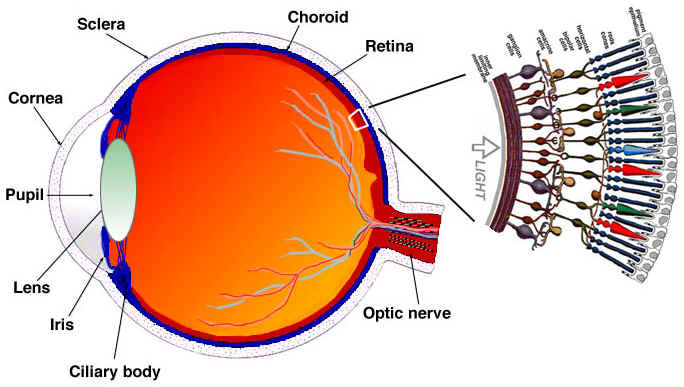
눈은 복잡한 장기이며, 많은 것들로 구성되어 있으나 여기서는 대부분은 원추세포와 간상세포에 집중합니다. 눈은 약 1억 2천개의 간상세포와 6백만개의 원추세포로 구성되어 있습니다. 더 간단하게 설명하기 위해, 색상과 명암을 눈의 각 기능들에 입력한다고 가정해봅시다. 간상세포 는 대부분 빛에 반응하는 반면에, 원추세포는 색상에 반응합니다. 서로 다른 색소를 지닌 세 가지 타입의 원추 세포가 존재합니다: S-cones (파란색), M-cones (초록색) and L-cones (빨간색).

간상 세포(명암)가 원추 세포(색상)보다 많기 때문에, 색상보다 명암을 더 잘 구분할 것이라는 사실을 짐작할 수 있을 것입니다.

eyes composition

대비 인식 능력

실험 심리학 및 다른 분야들의 연구자들은 사람의 시각에 대한 많은 이론을 개발했습니다. 그 중 하나를 대비 인식 능력이라고 부릅니다. 이것들은 빛의 공간과 시간과 관련 있으며, 주어진 초기에 관측한 빛이 나타내는 값이, 관측자가 변화가 있다는 사실을 말하기까지 얼마나 많은 변화가 필요한지에 대한 것입니다. function이 복수형으로 되어 있는데, 그 이유는 바로 대비 인식 능력은 명암 뿐만 아니라 색상도 관계되어 있기 때문입니다. 이 실험의 결과는 대부분의 경우에 우리의 눈이 색상보다 명암에 더 민감하다는 사실을 말해줍니다.

이제 루마(이미지의 명도)에 더 민감하다는 사실을 알게되었으므로 이를 이용해볼 수 있습니다.

색상 모델

초반에 배웠던 RGB 모델을 이용한 이미지에 색상 지정하는 방법외에도 다른 모델들도 있다는 것을 배웠습니다. 사실 모델 중 크로미넌스(색상)로부터 루마(명도)를 분리하는 모델이 있습니다. 이는 YCbCr*이라고도 알려져있습니다.

* 이와 같은 방식을 사용하는 다른 모델들도 존재합니다.

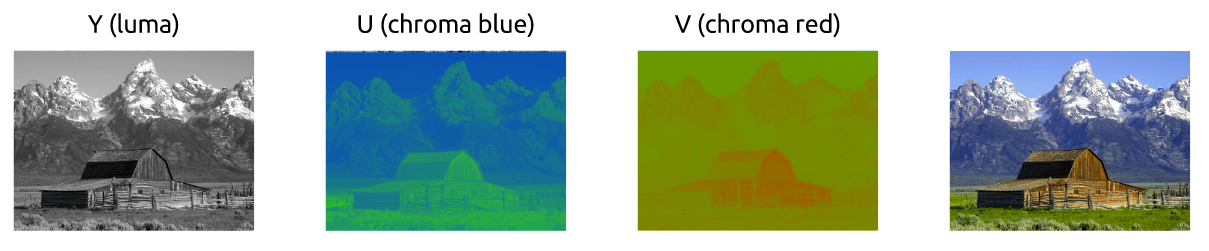
이 색상 모델은 명도를 표현하는 Y와 두 가지 색상 채널인 Cb(크로마 블루)와 Cr(크로마 레드)를 사용합니다. YCbCr은 RGB로부터 유도 가능하며, 또한 반대로 RGB로 역변환도 가능합니다. 이 모델을 사용하여 아래에 보이는 이미지와 같은 완전한 색상의 이미지를 만들 수 있습니다.

ycbcr example

YCbCr <-> RGB 변환

논쟁이 있을 수 있는데요, 어떻게 초록색을 사용하지 않고 모든 색상을 표현할 수 있을까요?

이 질문에 답하기 위해 RGB를 YCbCr로 변환하는 일을 같이 해봅시다. ITU-R 그룹* 에서 권장하는 표준 BT.601 계수를 사용할 것입니다. 첫 번째 단계는 루마 계산입니다. ITU에서 제안한 상수를 사용하고 RGB 값을 대체할 것입니다.

Y = 0.299R + 0.587G + 0.114B

루마를 얻었으니 이제 색상 분리(크로마 블루, 크로마 레드)를 할 수 있습니다:

Cb = 0.564(B - Y)
Cr = 0.713(R - Y)

또한 이를 역변환 가능하며 YCbCr을 사용하여 초록색을 얻을 수도 있습니다.

R = Y + 1.402Cr
B = Y + 1.772Cb
G = Y - 0.344Cb - 0.714Cr

* 무엇이 표준인지 정의합니다. 가령 4K란 무엇인가? 어떤 프레임 레이트를 사용해야 하는가? 해상도는? 컬러 모델은?과 같은 것들입니다.
일반적으로 디스플레이(모니터, TV, 스크린 등)는 오직 RGB 모델만 활용하며 이를 각자 다른 방식으로 배열합니다. 확대된 모습은 다음과 같습니다:

pixel geometry

크로마 서브샘플링

루마와 크로마로 표현되는 이미지를 인간의 시각이 크로마보다 루마 해상도에 민감하다는 사실을 이용하여 선택적으로 정보를 제거하는데에 있어 이점을 취할 수 있습니다. 크로마 서브샘플링은 루마 대비 크로마 정보를 줄여 이미지를 인코딩하는 기술입니다.

ycbcr subsampling resolutions

얼마만큼의 크로마 해상도를 줄여야 하는 것일까요?! 이미 답은 나와 있습니다. 해상도와 병합(final color = Y + Cb + Cr)을 다루는 스키마가 이미 존재합니다.

이러한 스키마는 서브 샘플링 시스템으로 알려져있으며 루마 픽셀의 a x 2 블록에 대한 크로마 해상도를 정의하는 3 부분의 비율 a:x:y로 정의됩니다.

  • a는 수평 샘플링 레퍼런스입니다. (일반적으로 4)
  • x는 a 픽셀의 행(row)의 크로마 샘플 수입니다. (a에 대한 수평해상도)
  • y는 a 픽셀의 첫 번째와 두 번째 행 사이의 크로마 샘플의 변화에 대한 개수입니다.

예외적으로 4:1:0은 각각의 루마 해상도의 4 x 4블록 내의 단일 크로마 샘플을 제공합니다.

현대 코덱에 사용되는 보편적인 기법은 4:4:4(서브 샘플링 없음), 4:2:2, 4:1:1, 4:2:0, 4:1:0 and 3:1:1입니다.

YCbCr 4:2:0 병합

여기에 YCbCr 4:2:0을 사용한 이미지의 병합된 조각입니다. 픽셀 당 12 비트만 소모했을 뿐이라는 사실을 기억하세요.

YCbCr 4:2:0 merge

동일한 이미지에 대해 주요한 크로마 서브샘플링 타입들로 인코딩한 이미지를 보실 수 있을겁니다. 첫 번째 행의 이미지들은 최종 YCbCr 이미지이며 두 번째 열의 이미지들은 크로마 해상도를 나타냅니다. 적은 손실로 훌륭한 결과를 얻었습니다.

chroma subsampling examples

앞서 우리는 한 시간 분량의 720p 해상도에 30fps인 영상을 저장하기 위해 278GB가 필요하다고 계산하였습니다. YCbCr 4:2:0을 사용하면 이를 절반(139GB)의 크기*로 줄일 수 있습니다. 하지만 아직 그리 이상적이진 않네요.

* 이 값은 width, height, 픽셀 당 비트 수 그리고 fps를 곱하여 얻었습니다. 이전에는 24비트가 필요했지만 이젠 12비트면 됩니다.


실습: YCbCr 히스토그램 확인하기

ffmpeg로 YCbCr 히스토그램을 확인할 수 있습니다. 이 장면은 히스토그램에 보여지는 바와 같이 파란색 비율이 높습니다.

ycbcr color histogram

프레임 유형

이제 계속해서 시간 상에서의 중복 제거를 할 수도 있지만 그 전에 몇 가지 기본적인 용어를 정립해보겠습니다. 30fps의 영화가 있다고 가정해봅시다. 여기에 이 영화의 첫 번째부분의 4장의 프레임이 있습니다.

ball 1 ball 2 ball 3 ball 4

파란색 배경과 같이 프레임 내에 많은 중복을 볼 수 있을겁니다. 프레임 0부터 3까지 변한게 없지요. 이 문제를 해결하기 위해 프레임을 세 가지 유형으로 추상적으로 분류할 수 있습니다.

I Frame (인트라, 키프레임)

I-frame(레퍼런스, 키프레임, 인트라)은 자기 자신을 포함한 프레임입니다. 렌더링 하기 위해 어떤 것에도 의존적이지 않지요. I-frame은 마치 정적인 사진같습니다. 첫 번째 프레임은 보통 I-frame입니다. 하지만 I-frame은 일반적으로 다른 유형의 프레임의 사이사이에 삽입된다는 사실을 볼 수 있을 겁니다.

ball 1

P Frame (predicted)

P-frame은 거의 항상 이전의 프레임을 이용하여 렌더링 될 수 있다는 점을 이점으로 취할 수 있습니다. 예를ㄷ를어 두 번째 프레임에서 변화라곤 공이 앞으로 움직인 것 뿐입니다. 변경된 부분을 사용해서 이 전의 프레임을 참고하여 프레임 1번을 다시 만들 수 있지요.

ball 1 <- ball 2

실습: I-frame이 한장 뿐인 동영상

P-frame이 데이터를 적게 사용하는데 왜 전체를 I-frame 한장에 나머지 전부가 p-frame인 영상으로 인코딩하지 않을까요?

이 비디오를 인코딩하고 영상을 시작해서 비디오의 앞부분으로 이동해보면, 이동하는데 시간이 좀 걸리는 사실을 알게될겁니다. 왜냐하면 P-frame은 렌더링하기 위해 레퍼런스 프레임(가령 I-frame)이 필요하기 때문입니다.

빨리 테스트 해볼 수 있는 다른 방법은 I-frame 한 장으로 비디오를 인코딩한 뒤, 2초 간격으로 I-frame을 삽입하여 인코딩한 뒤 각 렌디션의 사이즈를 확인해보세요.

B Frame (bi-predictive)

이전과 앞의 프레임을 참조하여 더 나은 압축률을 제공할 수 있다면?! 그것이 바로 B-Frame이라는 것입니다.

ball 1 <- ball 2 -> ball 3

실습: B-frame으로 비디오 비교하기

두 개의 렌디션을 생성해, 첫 번째에는 B-frame을 주고 다른 것에는 B-frame을 주지 않고 퀄리티를 비롯하여 파일 사이즈도 확인을 해보세요.

요약

이러한 프레임들은 더 나은 압축 성능을 제공하는데 사용됩니다. 어떻게 이런 일이 가능한지 다음 섹션에서 알아볼 거에요. 하지만 여러분은 이제 I-frame은 코스트가 높고 P-frame은 좀 더 낮고 B-frame이 제일 낮다는 사실에 대해 생각할 수 있게 되었습니다.

frame types example

Temporal redundancy (inter prediction)

Let's explore the options we have to reduce the repetitions in time, this type of redundancy can be solved with techniques of inter prediction.

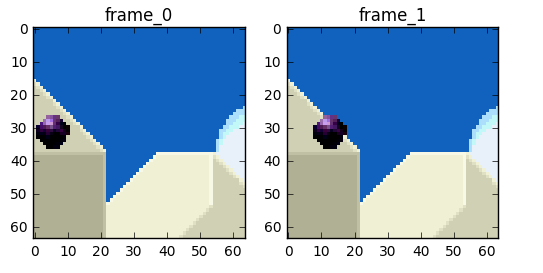
We will try to spend fewer bits to encode the sequence of frames 0 and 1.

original frames

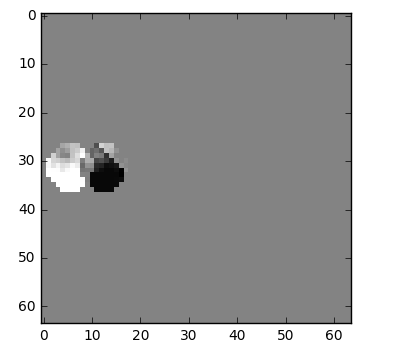
One thing we can do it's a subtraction, we simply subtract frame 1 from frame 0 and we get just what we need to encode the residual.

delta frames

But what if I tell you that there is a better method which uses even fewer bits?! First, let's treat the frame 0 as a collection of well-defined partitions and then we'll try to match the blocks from frame 0 on frame 1. We can think of it as motion estimation.

Wikipedia - block motion compensation

"Block motion compensation divides up the current frame into non-overlapping blocks, and the motion compensation vector tells where those blocks come from (a common misconception is that the previous frame is divided up into non-overlapping blocks, and the motion compensation vectors tell where those blocks move to). The source blocks typically overlap in the source frame. Some video compression algorithms assemble the current frame out of pieces of several different previously-transmitted frames."

delta frames

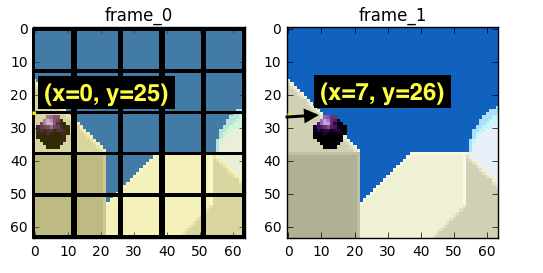
We could estimate that the ball moved from x=0, y=25 to x=6, y=26, the x and y values are the motion vectors. One further step we can do to save bits is to encode only the motion vector difference between the last block position and the predicted, so the final motion vector would be x=6 (6-0), y=1 (26-25)

In a real-world situation, this ball would be sliced into n partitions but the process is the same.

The objects on the frame move in a 3D way, the ball can become smaller when it moves to the background. It's normal that we won't find the perfect match to the block we tried to find a match. Here's a superposed view of our estimation vs the real picture.

motion estimation

But we can see that when we apply motion estimation the data to encode is smaller than using simply delta frame techniques.

motion estimation vs delta

How real motion compensation would look

This technique is applied to all blocks, very often a ball would be partitioned in more than one block. real world motion compensation Source: https://web.stanford.edu/class/ee398a/handouts/lectures/EE398a_MotionEstimation_2012.pdf

You can play around with these concepts using jupyter.

Hands-on: See the motion vectors

We can generate a video with the inter prediction (motion vectors) with ffmpeg.

inter prediction (motion vectors) with ffmpeg

Or we can use the Intel Video Pro Analyzer (which is paid but there is a free trial version which limits you to only the first 10 frames).

inter prediction intel video pro analyzer

Spatial redundancy (intra prediction)

If we analyze each frame in a video we'll see that there are also many areas that are correlated.

Let's walk through an example. This scene is mostly composed of blue and white colors.

This is an I-frame and we can't use previous frames to predict from but we still can compress it. We will encode the red block selection. If we look at its neighbors, we can estimate that there is a trend of colors around it.

We will predict that the frame will continue to spread the colors vertically, it means that the colors of the unknown pixels will hold the values of its neighbors.

Our prediction can be wrong, for that reason we need to apply this technique (intra prediction) and then subtract the real values which gives us the residual block, resulting in a much more compressible matrix compared to the original.

Hands-on: Check intra predictions

You can generate a video with macro blocks and their predictions with ffmpeg. Please check the ffmpeg documentation to understand the meaning of each block color.

intra prediction (macro blocks) with ffmpeg

Or we can use the Intel Video Pro Analyzer (which is paid but there is a free trial version which limits you to only the first 10 frames).

intra prediction intel video pro analyzer

How does a video codec work?

What? Why? How?

What? It's a piece of software / hardware that compresses or decompresses digital video. Why? Market and society demands higher quality videos with limited bandwidth or storage. Remember when we calculated the needed bandwidth for 30 frames per second, 24 bits per pixel, resolution of a 480x240 video? It was 82.944 Mbps with no compression applied. It's the only way to deliver HD/FullHD/4K in TVs and the Internet. How? We'll take a brief look at the major techniques here.

CODEC vs Container

One common mistake that beginners often do is to confuse digital video CODEC and digital video container. We can think of containers as a wrapper format which contains metadata of the video (and possible audio too), and the compressed video can be seen as its payload.

Usually, the extension of a video file defines its video container. For instance, the file video.mp4 is probably a MPEG-4 Part 14 container and a file named video.mkv it's probably a matroska. To be completely sure about the codec and container format we can use ffmpeg or mediainfo.

History

Before we jump into the inner workings of a generic codec, let's look back to understand a little better about some old video codecs.

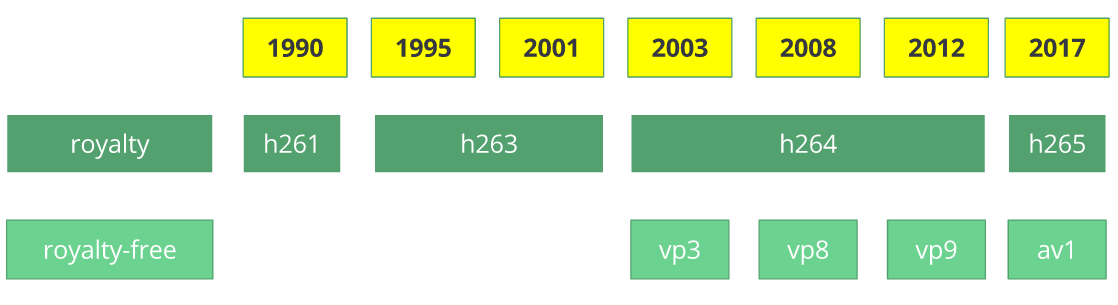
The video codec H.261 was born in 1990 (technically 1988), and it was designed to work with data rates of 64 kbit/s. It already uses ideas such as chroma subsampling, macro block, etc. In the year of 1995, the H.263 video codec standard was published and continued to be extended until 2001.

In 2003 the first version of H.264/AVC was completed. In the same year, a company called TrueMotion released their video codec as a royalty-free lossy video compression called VP3. In 2008, Google bought this company, releasing VP8 in the same year. In December of 2012, Google released the VP9 and it's supported by roughly ¾ of the browser market (mobile included).

AV1 is a new royalty-free and open source video codec that's being designed by the Alliance for Open Media (AOMedia), which is composed of the companies: Google, Mozilla, Microsoft, Amazon, Netflix, AMD, ARM, NVidia, Intel and Cisco among others. The first version 0.1.0 of the reference codec was published on April 7, 2016.

codec history timeline

The birth of AV1

Early 2015, Google was working on VP10, Xiph (Mozilla) was working on Daala and Cisco open-sourced its royalty-free video codec called Thor.

Then MPEG LA first announced annual caps for HEVC (H.265) and fees 8 times higher than H.264 but soon they changed the rules again:

  • no annual cap,
  • content fee (0.5% of revenue) and
  • per-unit fees about 10 times higher than h264.

The alliance for open media was created by companies from hardware manufacturer (Intel, AMD, ARM , Nvidia, Cisco), content delivery (Google, Netflix, Amazon), browser maintainers (Google, Mozilla), and others.

The companies had a common goal, a royalty-free video codec and then AV1 was born with a much simpler patent license. Timothy B. Terriberry did an awesome presentation, which is the source of this section, about the AV1 conception, license model and its current state.

You'll be surprised to know that you can analyze the AV1 codec through your browser, go to http://aomanalyzer.org/

av1 browser analyzer

PS: If you want to learn more about the history of the codecs you must learn the basics behind video compression patents.

A generic codec

We're going to introduce the main mechanics behind a generic video codec but most of these concepts are useful and used in modern codecs such as VP9, AV1 and HEVC. Be sure to understand that we're going to simplify things a LOT. Sometimes we'll use a real example (mostly H.264) to demonstrate a technique.

1st step - picture partitioning

The first step is to divide the frame into several partitions, sub-partitions and beyond.

picture partitioning

But why? There are many reasons, for instance, when we split the picture we can work the predictions more precisely, using small partitions for the small moving parts while using bigger partitions to a static background.

Usually, the CODECs organize these partitions into slices (or tiles), macro (or coding tree units) and many sub-partitions. The max size of these partitions varies, HEVC sets 64x64 while AVC uses 16x16 but the sub-partitions can reach sizes of 4x4.

Remember that we learned how frames are typed?! Well, you can apply those ideas to blocks too, therefore we can have I-Slice, B-Slice, I-Macroblock and etc.

Hands-on: Check partitions

We can also use the Intel Video Pro Analyzer (which is paid but there is a free trial version which limits you to only the first 10 frames). Here are VP9 partitions analyzed.

VP9 partitions view intel video pro analyzer

2nd step - predictions

Once we have the partitions, we can make predictions over them. For the inter prediction we need to send the motion vectors and the residual and the intra prediction we'll send the prediction direction and the residual as well.

3rd step - transform

After we get the residual block (predicted partition - real partition), we can transform it in a way that lets us know which pixels we can discard while keeping the overall quality. There are some transformations for this exact behavior.

Although there are other transformations, we'll look more closely at the discrete cosine transform (DCT). The DCT main features are:

  • converts blocks of pixels into same-sized blocks of frequency coefficients.
  • compacts energy, making it easy to eliminate spatial redundancy.
  • is reversible, a.k.a. you can reverse to pixels.

On 2 Feb 2017, Cintra, R. J. and Bayer, F. M have published their paper DCT-like Transform for Image Compression Requires 14 Additions Only.

Don't worry if you didn't understand the benefits from every bullet point, we'll try to make some experiments in order to see the real value from it.

Let's take the following block of pixels (8x8):

pixel values matrix

Which renders to the following block image (8x8):

pixel values matrix

When we apply the DCT over this block of pixels and we get the block of coefficients (8x8):

coefficients values

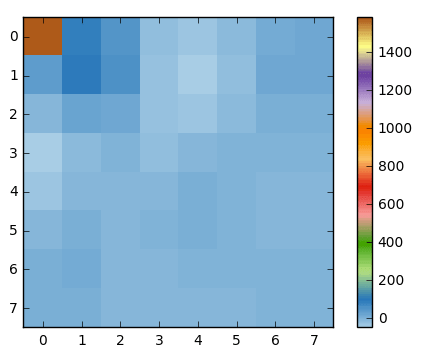
And if we render this block of coefficients, we'll get this image:

dct coefficients image

As you can see it looks nothing like the original image, we might notice that the first coefficient is very different from all the others. This first coefficient is known as the DC coefficient which represents of all the samples in the input array, something similar to an average.

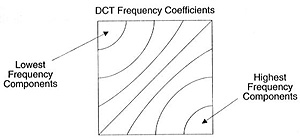
This block of coefficients has an interesting property which is that it separates the high-frequency components from the low frequency.

dct frequency coefficients property

In an image, most of the energy will be concentrated in the lower frequencies, so if we transform an image into its frequency components and throw away the higher frequency coefficients, we can reduce the amount of data needed to describe the image without sacrificing too much image quality.

frequency means how fast a signal is changing

Let's try to apply the knowledge we acquired in the test by converting the original image to its frequency (block of coefficients) using DCT and then throwing away part of the least important coefficients.

First, we convert it to its frequency domain.

coefficients values

Next, we discard part (67%) of the coefficients, mostly the bottom right part of it.

zeroed coefficients

Finally, we reconstruct the image from this discarded block of coefficients (remember, it needs to be reversible) and compare it to the original.

original vs quantized

As we can see it resembles the original image but it introduced lots of differences from the original, we throw away 67.1875% and we still were able to get at least something similar to the original. We could more intelligently discard the coefficients to have a better image quality but that's the next topic.

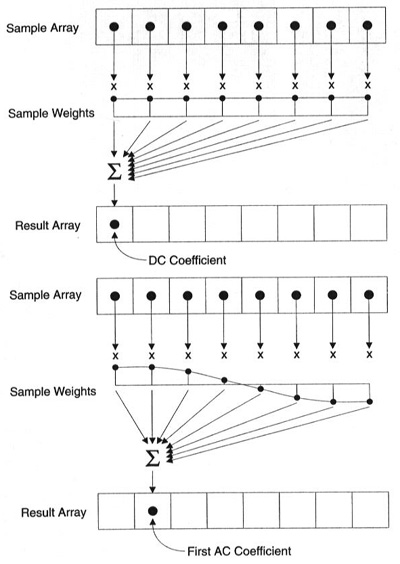
Each coefficient is formed using all the pixels

It's important to note that each coefficient doesn't directly map to a single pixel but it's a weighted sum of all pixels. This amazing graph shows how the first and second coefficient is calculated, using weights which are unique for each index.

dct calculation

Source: https://web.archive.org/web/20150129171151/https://www.iem.thm.de/telekom-labor/zinke/mk/mpeg2beg/whatisit.htm

You can also try to visualize the DCT by looking at a simple image formation over the DCT basis. For instance, here's the A character being formed using each coefficient weight.


Hands-on: throwing away different coefficients

You can play around with the DCT transform.

4th step - quantization

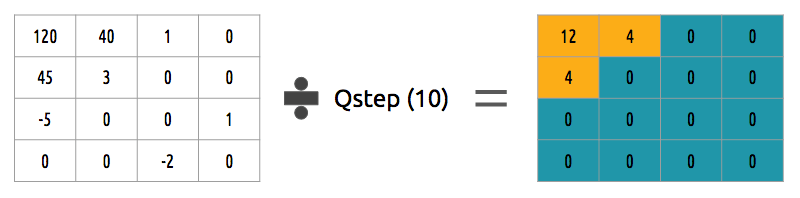
When we throw away some of the coefficients, in the last step (transform), we kinda did some form of quantization. This step is where we chose to lose information (the lossy part) or in simple terms, we'll quantize coefficients to achieve compression.

How can we quantize a block of coefficients? One simple method would be a uniform quantization, where we take a block, divide it by a single value (10) and round this value.

quantize

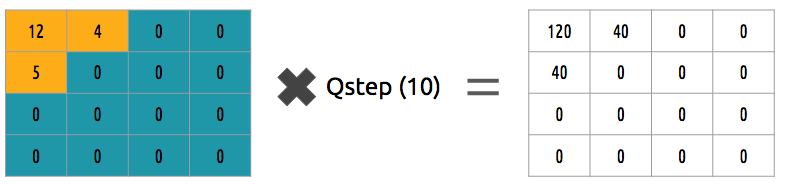
How can we reverse (re-quantize) this block of coefficients? We can do that by multiplying the same value (10) we divide it first.

re-quantize

This approach isn't the best because it doesn't take into account the importance of each coefficient, we could use a matrix of quantizers instead of a single value, this matrix can exploit the property of the DCT, quantizing most the bottom right and less the upper left, the JPEG uses a similar approach, you can check source code to see this matrix.

Hands-on: quantization

You can play around with the quantization.

5th step - entropy coding

After we quantized the data (image blocks/slices/frames) we still can compress it in a lossless way. There are many ways (algorithms) to compress data. We're going to briefly experience some of them, for a deeper understanding you can read the amazing book Understanding Compression: Data Compression for Modern Developers.

VLC coding:

Let's suppose we have a stream of the symbols: a, e, r and t and their probability (from 0 to 1) is represented by this table.

a e r t
probability 0.3 0.3 0.2 0.2

We can assign unique binary codes (preferable small) to the most probable and bigger codes to the least probable ones.

a e r t
probability 0.3 0.3 0.2 0.2
binary code 0 10 110 1110

Let's compress the stream eat, assuming we would spend 8 bits for each symbol, we would spend 24 bits without any compression. But in case we replace each symbol for its code we can save space.

The first step is to encode the symbol e which is 10 and the second symbol is a which is added (not in a mathematical way) [10][0] and finally the third symbol t which makes our final compressed bitstream to be [10][0][1110] or 1001110 which only requires 7 bits (3.4 times less space than the original).

Notice that each code must be a unique prefixed code Huffman can help you to find these numbers. Though it has some issues there are video codecs that still offers this method and it's the algorithm for many applications which requires compression.

Both encoder and decoder must know the symbol table with its code, therefore, you need to send the table too.

Arithmetic coding:

Let's suppose we have a stream of the symbols: a, e, r, s and t and their probability is represented by this table.

a e r s t
probability 0.3 0.3 0.15 0.05 0.2

With this table in mind, we can build ranges containing all the possible symbols sorted by the most frequents.

initial arithmetic range

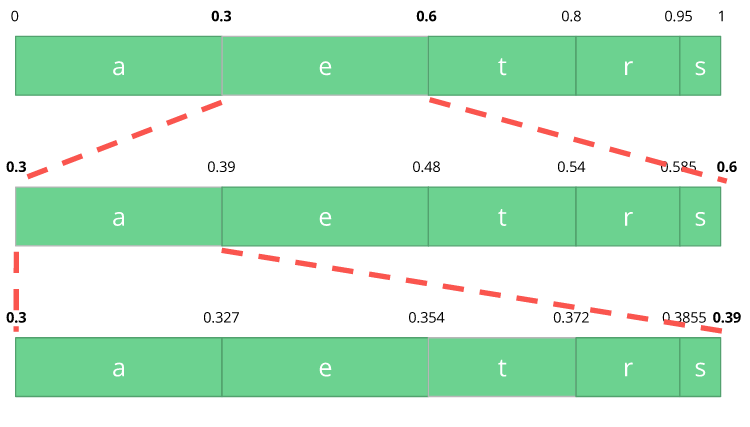
Now let's encode the stream eat, we pick the first symbol e which is located within the subrange 0.3 to 0.6 (but not included) and we take this subrange and split it again using the same proportions used before but within this new range.

second sub range

Let's continue to encode our stream eat, now we take the second symbol a which is within the new subrange 0.3 to 0.39 and then we take our last symbol t and we do the same process again and we get the last subrange 0.354 to 0.372.

final arithmetic range

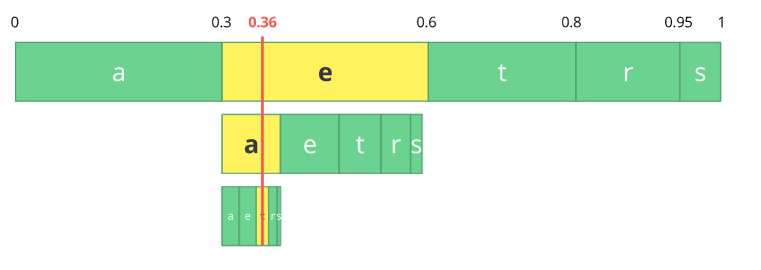
We just need to pick a number within the last subrange 0.354 to 0.372, let's choose 0.36 but we could choose any number within this subrange. With only this number we'll be able to recover our original stream eat. If you think about it, it's like if we were drawing a line within ranges of ranges to encode our stream.

final range traverse

The reverse process (A.K.A. decoding) is equally easy, with our number 0.36 and our original range we can run the same process but now using this number to reveal the stream encoded behind this number.

With the first range, we notice that our number fits at the slice, therefore, it's our first symbol, now we split this subrange again, doing the same process as before, and we'll notice that 0.36 fits the symbol a and after we repeat the process we came to the last symbol t (forming our original encoded stream eat).

Both encoder and decoder must know the symbol probability table, therefore you need to send the table.

Pretty neat, isn't it? People are damn smart to come up with a such solution, some video codecs use this technique (or at least offer it as an option).

The idea is to lossless compress the quantized bitstream, for sure this article is missing tons of details, reasons, trade-offs and etc. But you should learn more as a developer. Newer codecs are trying to use different entropy coding algorithms like ANS.

Hands-on: CABAC vs CAVLC

You can generate two streams, one with CABAC and other with CAVLC and compare the time it took to generate each of them as well as the final size.

6th step - bitstream format

After we did all these steps we need to pack the compressed frames and context to these steps. We need to explicitly inform to the decoder about the decisions taken by the encoder, such as bit depth, color space, resolution, predictions info (motion vectors, intra prediction direction), profile, level, frame rate, frame type, frame number and much more.

We're going to study, superficially, the H.264 bitstream. Our first step is to generate a minimal H.264 * bitstream, we can do that using our own repository and ffmpeg.

./s/ffmpeg -i /files/i/minimal.png -pix_fmt yuv420p /files/v/minimal_yuv420.h264

* ffmpeg adds, by default, all the encoding parameter as a SEI NAL, soon we'll define what is a NAL.

This command will generate a raw h264 bitstream with a single frame, 64x64, with color space yuv420 and using the following image as the frame.

used frame to generate minimal h264 bitstream

H.264 bitstream

The AVC (H.264) standard defines that the information will be sent in macro frames (in the network sense), called NAL (Network Abstraction Layer). The main goal of the NAL is the provision of a "network-friendly" video representation, this standard must work on TVs (stream based), the Internet (packet based) among others.

NAL units H.264

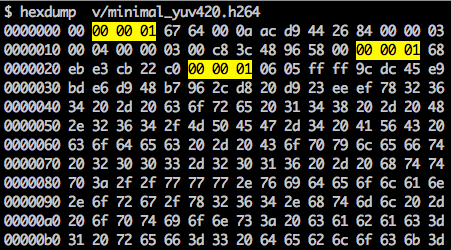
There is a synchronization marker to define the boundaries of the NAL's units. Each synchronization marker holds a value of 0x00 0x00 0x01 except to the very first one which is 0x00 0x00 0x00 0x01. If we run the hexdump on the generated h264 bitstream, we can identify at least three NALs in the beginning of the file.

synchronization marker on NAL units

As we said before, the decoder needs to know not only the picture data but also the details of the video, frame, colors, used parameters, and others. The first byte of each NAL defines its category and type.

NAL type id Description
0 Undefined
1 Coded slice of a non-IDR picture
2 Coded slice data partition A
3 Coded slice data partition B
4 Coded slice data partition C
5 IDR Coded slice of an IDR picture
6 SEI Supplemental enhancement information
7 SPS Sequence parameter set
8 PPS Picture parameter set
9 Access unit delimiter
10 End of sequence
11 End of stream
... ...

Usually, the first NAL of a bitstream is a SPS, this type of NAL is responsible for informing the general encoding variables like profile, level, resolution and others.

If we skip the first synchronization marker we can decode the first byte to know what type of NAL is the first one.

For instance the first byte after the synchronization marker is 01100111, where the first bit (0) is to the field forbidden_zero_bit, the next 2 bits (11) tell us the field nal_ref_idc which indicates whether this NAL is a reference field or not and the rest 5 bits (00111) inform us the field nal_unit_type, in this case, it's a SPS (7) NAL unit.

The second byte (binary=01100100, hex=0x64, dec=100) of an SPS NAL is the field profile_idc which shows the profile that the encoder has used, in this case, we used the constrained high-profile, it's a high profile without the support of B (bi-predictive) slices.

SPS binary view

When we read the H.264 bitstream spec for an SPS NAL we'll find many values for the parameter name, category and a description, for instance, let's look at pic_width_in_mbs_minus_1 and pic_height_in_map_units_minus_1 fields.

Parameter name Category Description
pic_width_in_mbs_minus_1 0 ue(v)
pic_height_in_map_units_minus_1 0 ue(v)

ue(v): unsigned integer Exp-Golomb-coded

If we do some math with the value of these fields we will end up with the resolution. We can represent a 1920 x 1080 using a pic_width_in_mbs_minus_1 with the value of 119 ( (119 + 1) * macroblock_size = 120 * 16 = 1920) , again saving space, instead of encode 1920 we did it with 119.

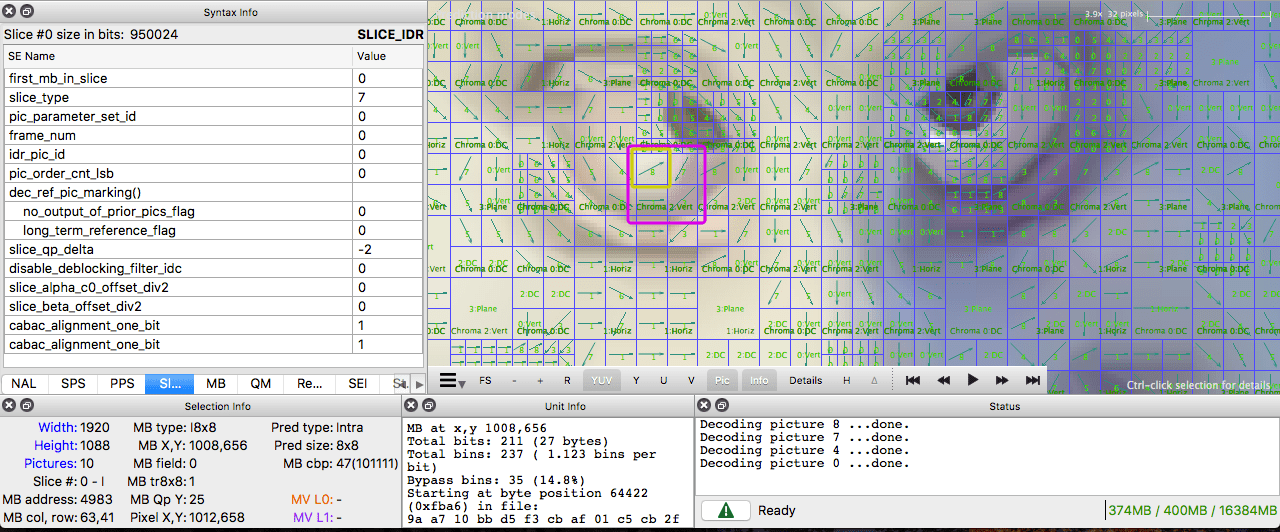
If we continue to examine our created video with a binary view (ex: xxd -b -c 11 v/minimal_yuv420.h264), we can skip to the last NAL which is the frame itself.

h264 idr slice header

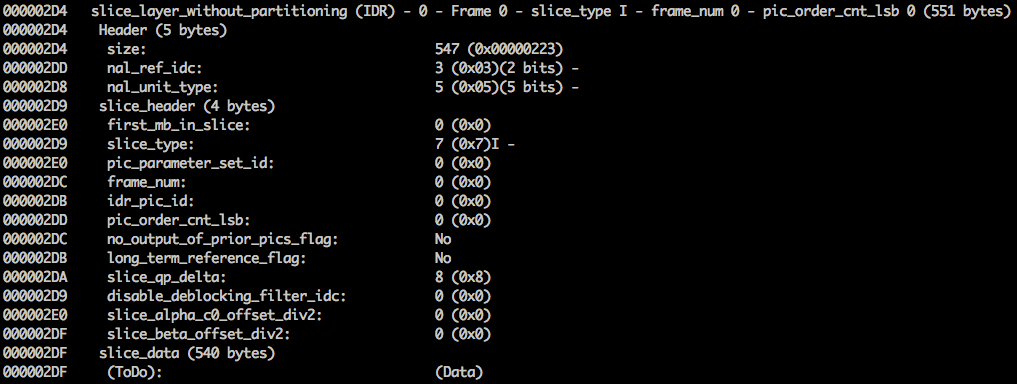
We can see its first 6 bytes values: 01100101 10001000 10000100 00000000 00100001 11111111. As we already know the first byte tell us about what type of NAL it is, in this case, (00101) it's an IDR Slice (5) and we can further inspect it:

h264 slice header spec

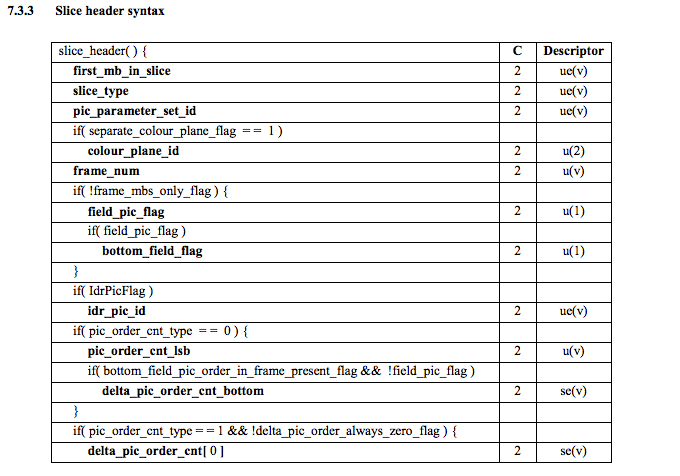
Using the spec info we can decode what type of slice (slice_type), the frame number (frame_num) among others important fields.

In order to get the values of some fields (ue(v), me(v), se(v) or te(v)) we need to decode it using a special decoder called Exponential-Golomb, this method is very efficient to encode variable values, mostly when there are many default values.

The values of slice_type and frame_num of this video are 7 (I slice) and 0 (the first frame).

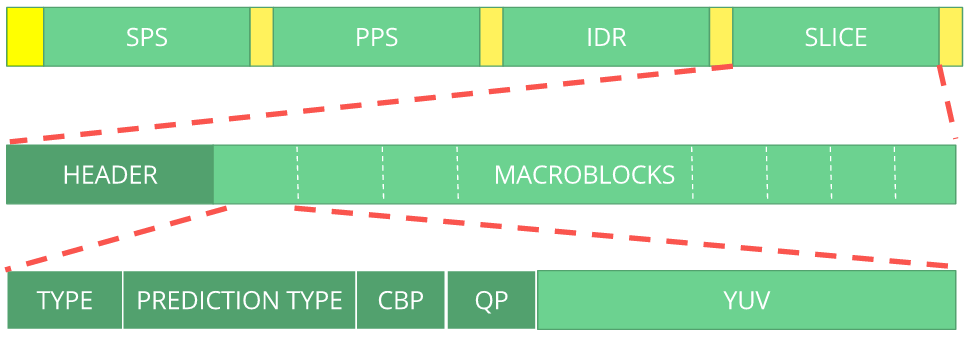
We can see the bitstream as a protocol and if you want or need to learn more about this bitstream please refer to the ITU H.264 spec. Here's a macro diagram which shows where the picture data (compressed YUV) resides.

h264 bitstream macro diagram

We can explore others bitstreams like the VP9 bitstream, H.265 (HEVC) or even our new best friend AV1 bitstream, do they all look similar? No, but once you learned one you can easily get the others.

Hands-on: Inspect the H.264 bitstream

We can generate a single frame video and use mediainfo to inspect its H.264 bitstream. In fact, you can even see the source code that parses h264 (AVC) bitstream.

mediainfo details h264 bitstream

We can also use the Intel Video Pro Analyzer which is paid but there is a free trial version which limits you to only the first 10 frames but that's okay for learning purposes.

intel video pro analyzer details h264 bitstream

Review

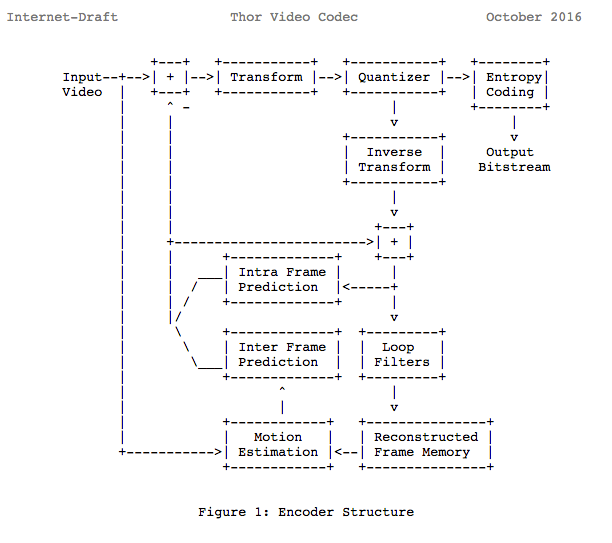
We'll notice that many of the modern codecs uses this same model we learned. In fact, let's look at the Thor video codec block diagram, it contains all the steps we studied. The idea is that you now should be able to at least understand better the innovations and papers for the area.

thor_codec_block_diagram

Previously we had calculated that we needed 139GB of storage to keep a video file with one hour at 720p resolution and 30fps if we use the techniques we learned here, like inter and intra prediction, transform, quantization, entropy coding and other we can achieve, assuming we are spending 0.031 bit per pixel, the same perceivable quality video requiring only 367.82MB vs 139GB of store.

We choose to use 0.031 bit per pixel based on the example video provided here.

How does H.265 achieve a better compression ratio than H.264?

Now that we know more about how codecs work, then it is easy to understand how new codecs are able to deliver higher resolutions with fewer bits.

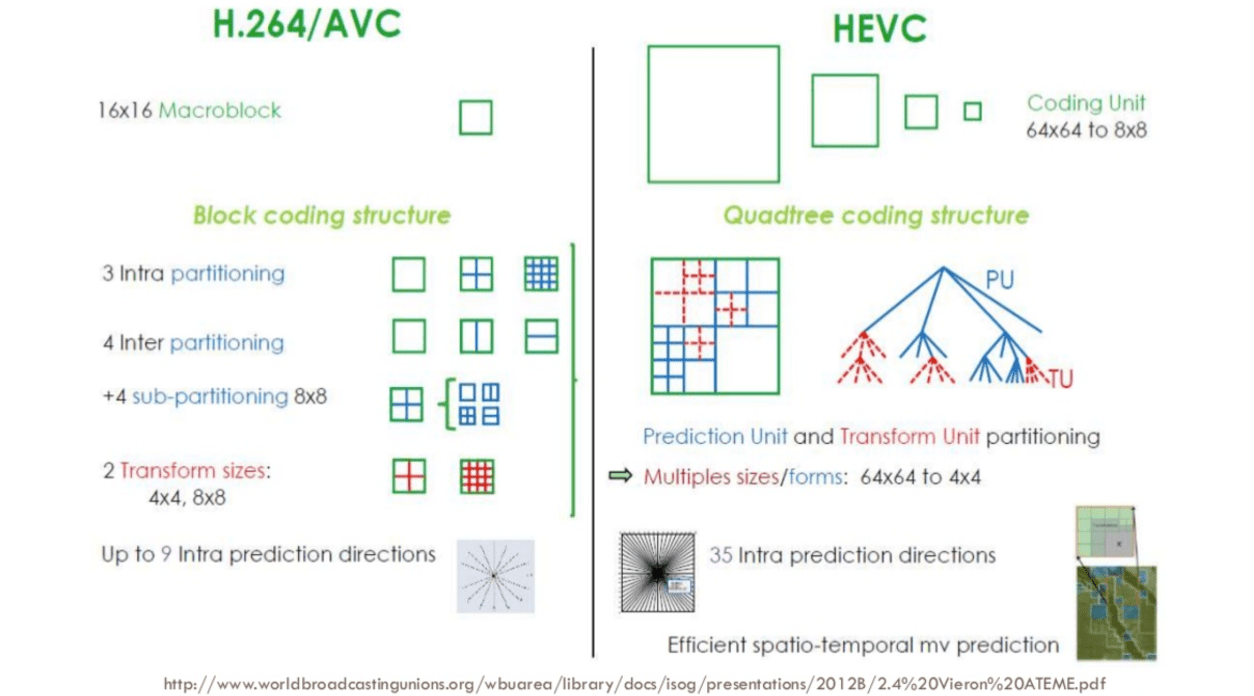
We will compare AVC and HEVC, let's keep in mind that it is almost always a trade-off between more CPU cycles (complexity) and compression rate.

HEVC has bigger and more partitions (and sub-partitions) options than AVC, more intra predictions directions, improved entropy coding and more, all these improvements made H.265 capable to compress 50% more than H.264.

h264 vs h265

Online streaming

General architecture

general architecture

[TODO]

Progressive download and adaptive streaming

progressive download

adaptive streaming

[TODO]

Content protection

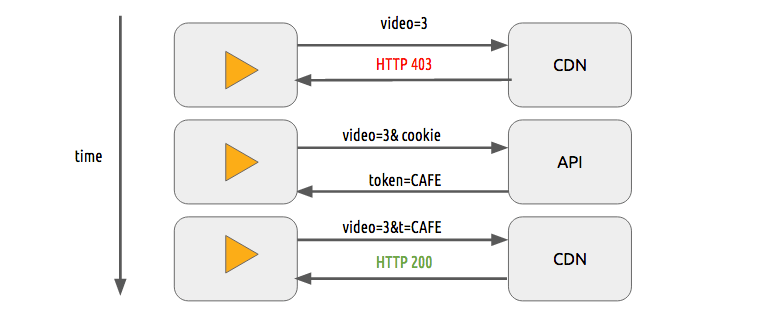
We can use a simple token system to protect the content. The user without a token tries to request a video and the CDN forbids her or him while a user with a valid token can play the content, it works pretty similarly to most of the web authentication systems.

token protection

The sole use of this token system still allows a user to download a video and distribute it. Then the DRM (digital rights management) systems can be used to try to avoid this.

drm

In real life production systems, people often use both techniques to provide authorization and authentication.

DRM

Main systems

What?

DRM means Digital rights management, it's a way to provide copyright protection for digital media, for instance, digital video and audio. Although it's used in many places it's not universally accepted.

Why?

Content creator (mostly studios) want to protect its intelectual property against copy to prevent unauthorized redistribution of digital media.

How?

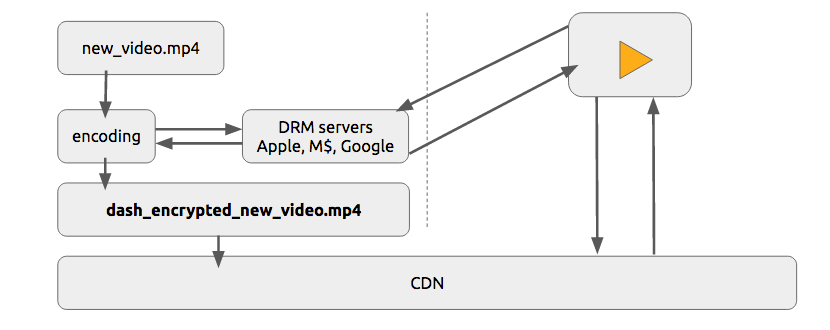
We're going to describe an abstract and generic form of DRM in a very simplified way.

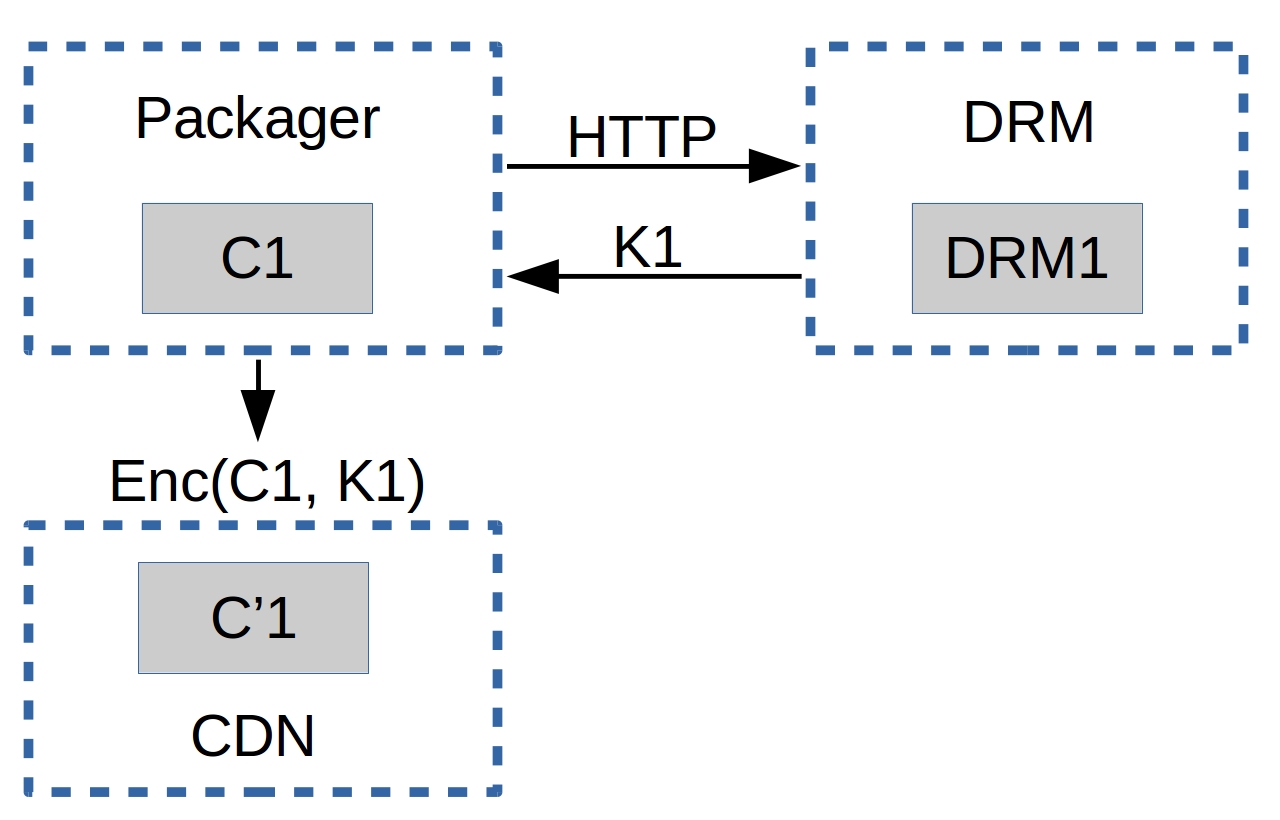
Given a content C1 (i.e. an hls or dash video streaming), with a player P1 (i.e. shaka-clappr, exo-player or ios) in a device D1 (i.e. a smartphone, TV, tablet or desktop/notebook) using a DRM system DRM1 (widevine, playready or FairPlay).

The content C1 is encrypted with a symmetric-key K1 from the system DRM1, generating the encrypted content C'1.

drm general flow

The player P1, of a device D1, has two keys (asymmetric), a private key PRK1 (this key is protected1 and only known by D1) and a public key PUK1.

1protected: this protection can be via hardware, for instance, this key can be stored inside a special (read-only) chip that works like a black-box to provide decryption, or by software (less safe), the DRM system provides means to know which type of protection a given device has.

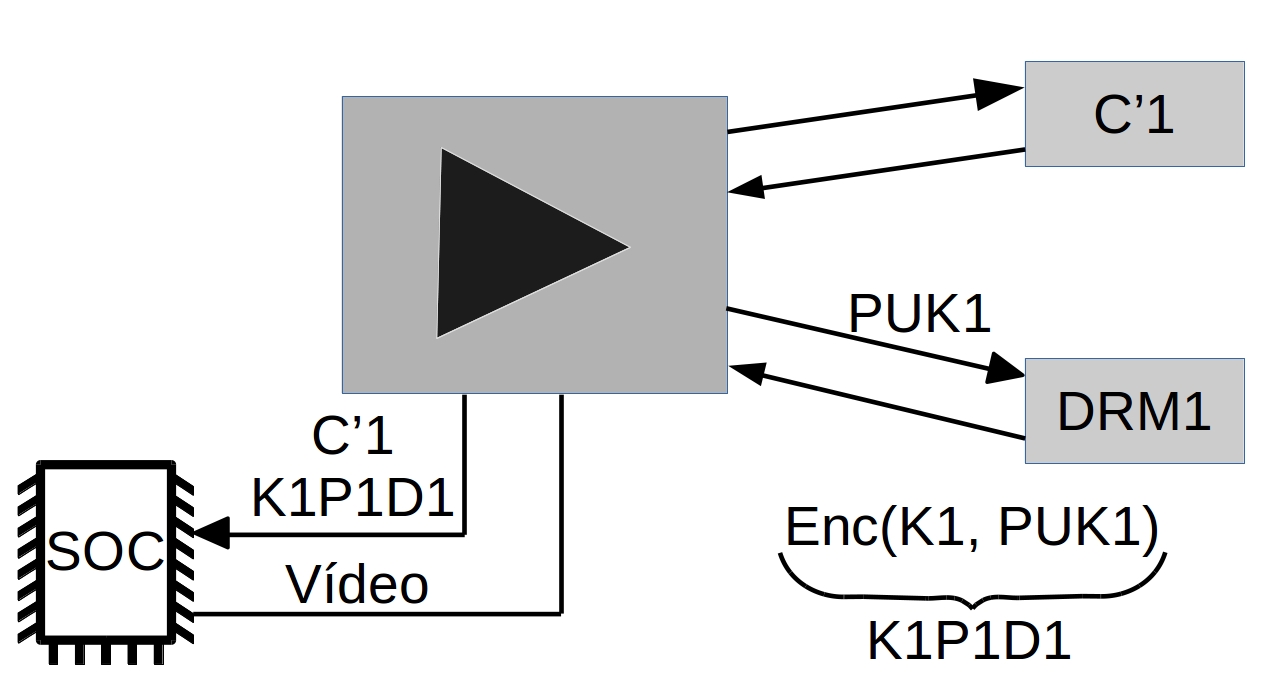
When the player P1 wants to play the content C'1, it needs to deal with the DRM system DRM1, giving its public key PUK1. The DRM system DRM1 returns the key K1 encrypted with the client''s public key PUK1. In theory, this response is something that only D1 is capable of decrypting.

K1P1D1 = enc(K1, PUK1)

P1 uses its DRM local system (it could be a SOC, a specialized hardware or software), this system is able to decrypt the content using its private key PRK1, it can decrypt the symmetric-key K1 from the K1P1D1 and play C'1. At best case, the keys are not exposed through RAM.

K1 = dec(K1P1D1, PRK1)

P1.play(dec(C'1, K1))

drm decoder flow

How to use jupyter

Make sure you have docker installed and just run ./s/start_jupyter.sh and follow the instructions on the terminal.

Conferences

References

The richest content is here, it's where all the info we saw in this text was extracted, based or inspired by. You can deepen your knowledge with these amazing links, books, videos and etc.

Online Courses and Tutorials:

Books:

Bitstream Specifications:

Software:

Non-ITU Codecs:

Encoding Concepts:

Video Sequences for Testing:

Miscellaneous: