You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
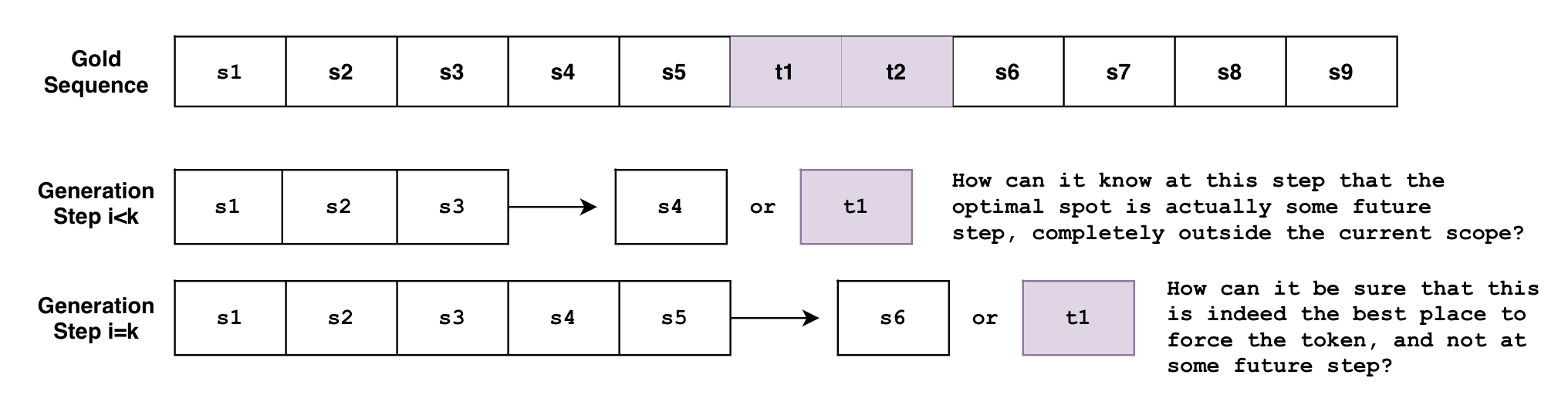
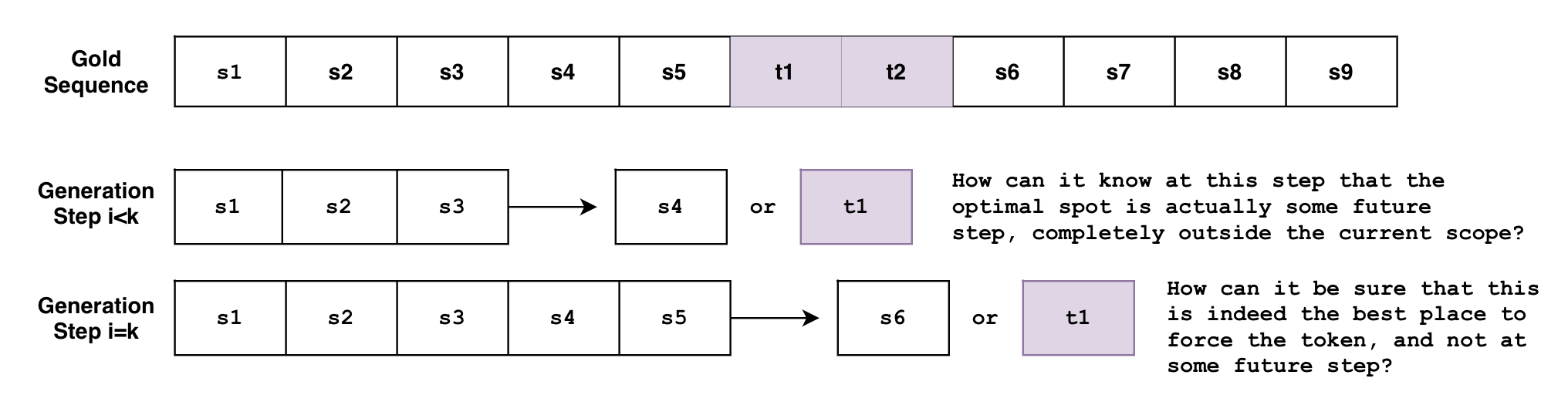
The problem is that beam search generates the sequence *token-by-token*. Though not entirely accurate, one can think of beam search as the function \\( B(\mathbf{s}_{0:i}) = s_{i+1} \\), where it looks as the currently generated sequence of tokens from \\( 0 \\) to \\( i \\) then predicts the next token at \\( i+1 \\) . But how can this function know, at an arbitrary step \\( i < k \\) , that the tokens must be generated at some future step \\( k \\) ? Or when it's at the step \\( i=k \\) , how can it know for sure that this is the best spot to force the tokens, instead of some future step \\( i>k \\) ?
48
48
49
-
49
+
50
50
51
51
52
52
And what if you have multiple constraints with varying requirements? What if you want to force the phrase \\( p_1=\{t_1, t_2\}\\) *and* also the phrase \\( p_2=\{ t_3, t_4, t_5, t_6\}\\) ? What if you want the model to **choose between** the two phrases? What if we want to force the phrase \\( p_1 \\) and force just one phrase among the list of phrases \\( \{p_{21}, p_{22}, p_{23}\}\\) ?
@@ -209,13 +209,13 @@ Unlike greedy search, beam search works by keeping a longer list of hypotheses.
209
209
210
210
Here's another way to look at the first step of the beam search for the above example, in the case of `num_beams=3`:
Instead of only choosing `"The dog"` like what a greedy search would do, a beam search would allow *further consideration* of `"The nice"` and `"The car"`.
215
215
216
216
In the next step, we consider the next possible tokens for each of the three branches we created in the previous step.
Though we end up *considering* significantly more than `num_beams` outputs, we reduce them down to `num_beams` at the end of the step. We can't just keep branching out, then the number of `beams` we'd have to keep track of would be \\( \text{beams}^{n} \\) for \\( n \\) steps, which becomes very large very quickly ( \\( 10 \\) beams after \\( 10 \\) steps is \\( 10,000,000,000 \\) beams!).
221
221
@@ -237,13 +237,13 @@ Let's say that we're trying to force the phrase `"is fast"` in the generation ou
237
237
In the traditional beam search setting, we find the top `k` most probable next tokens at each branch and append them for consideration. In the constrained setting, we do the same but also append the tokens that will take us *closer to fulfilling our constraints*. Here's a demonstration:
On top of the usual high-probability next tokens like `"dog"` and `"nice"`, we force the token `"is"` in order to get us closer to fulfilling our constraint of `"is fast"`.
243
243
244
244
For the next step, the branched-out candidates below are mostly the same as that of traditional beam search. But like the above example, constrained beam search adds onto the existing candidates by forcing the constraints at each new branch:
Notice how `"The is fast"` doesn't require any manual appending of constraint tokens since it's already fulfilled (i.e., already contains the phrase `"is fast"`). Also, notice how beams like `"The dog is slow"` or `"The dog is mad"` is actually in Bank 0, since, although it includes the token `"is"`, it must restart from the beginning to generate `"is fast"`. By appending something like `"slow"` after `"is"`, it has effectively *reset its progress*.
0 commit comments