Pohlig Hellman Algorithm

Prerequisites:

1. Discrete Logarithm Problem

Pohlig Hellman Algorithm is applicable in cases where order of the group, over which DLP is defined, is a smooth number (ie. the number that can be factored into small prime numbers). First, let us define our DLP over the Cyclic Group G = 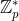having order n.

There are different variations to Pohlig-Hellman algorithm that can be applied in different conditions:

1. When order of a group is a power of 2 only ie. n = 2^e
2. When order of a group is a power of a prime ie. n = p^e, where p is a prime number
3. General algorithm ie. n = p₁^e₁ p₂^e₂ p₃^e₃... p_r^e_r

Order of a group is a power of 2

Source: https://crypto.stackexchange.com/questions/34180/discrete-logarithm-problem-is-easy-in-a-cyclic-group-of-order-a-power-of-two

I implemented this algorithm in python here: ph_orderp2.py

So if you have a group whose order is a power of 2, you can now solve the DLP in 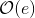, where e is the exponent in the group order n = 2^e.

Order of a group is a power of a prime number

Source: http://anh.cs.luc.edu/331/notes/PohligHellmanp_k2p.pdf

I implemented this algorithm in python here: ph_orderpp.py

General Algorithm

Source: http://anh.cs.luc.edu/331/notes/PohligHellmanp_k2p.pdf

I implemented this algorithm in python/sage here: pohlig_hellman.py