[TOC]
- layer. py : 代表的是神经网络的层,包含了该层线性变化和非线性变化(可以设置为没有)
- network. py : 根据输入的参数构建的神经网络,包含backward forward方法
- sin
- 文件夹都是数据
- train_network_sin.py : 训练神经网络的程序
- sin_data_model.py : 数据加载器
- experiencescript. py : 实验脚本代码
- trained_network.py : 加载训练好的模型
- img
- 文件夹都是数据
- dataloader. py
- imgdataset. py 以上为模仿pytorch 的dataset 和dataloader写的数据集处理机制
- train_network_img.py : 训练神经网络的程序
- experiencescript. py : 实验脚本代码
- trained_network=.py : 加载训练好的模型
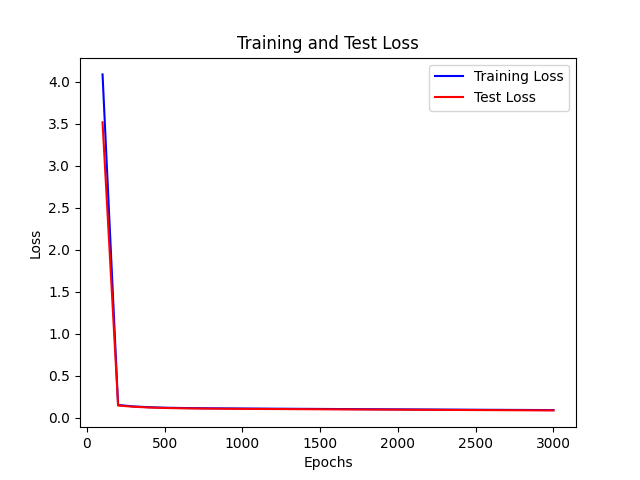
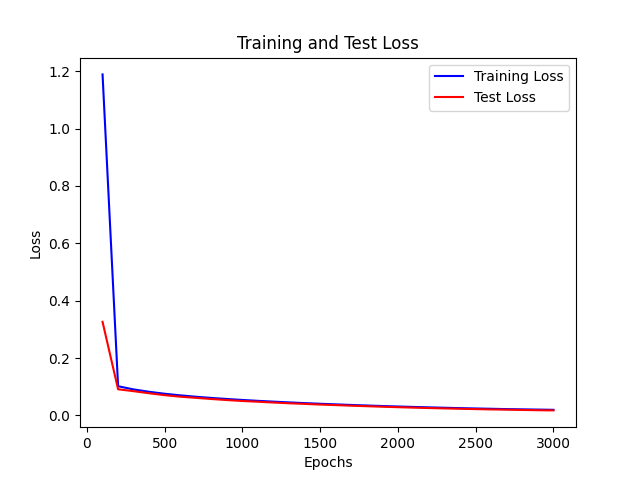
- 基于 单层 32unit sigmoid激活函数 实验
- 上图为lr为0.001 下图为 0.01 的情况
可见 对于sigmoid函数而言
lr太小的话,在部分epoch之后,loss会开始慢速下降,导致训练缓慢,所以需要较大的lr
| 图像 |
 |
 |
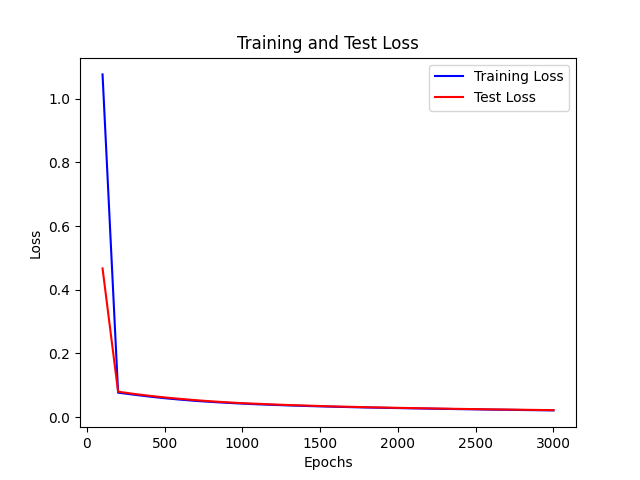
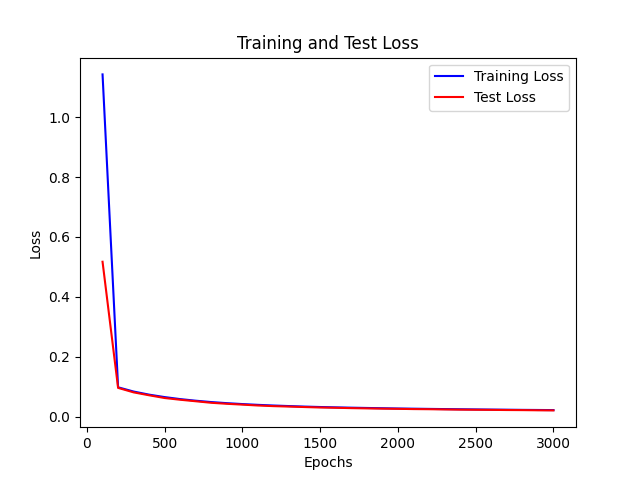
- 下面的两个网络在相同初始化情况下进行迭代
- 可见 正则项会惩罚过大的梯度,导致下降较慢,同时会防止过拟合
| 网络 |
L1误差 |
图像 |
| 正则项系数为0 |
Epoch 2900, Loss: 0.0208701047369986 |
 |
| 正则项系数为0.01 |
Epoch 2900, Loss: 0.022429724348479462 |
 |
- 实验:对两个不同网络同时进行十次测试 得到结果 取平均
- 可见单层网络收敛速度较快
- 双层网络更容易在不改变学习率的情况下不收敛
| 网络 |
3000epoch后的L1误差 |
| sigmoid 单层网络 |
0.014551067166471124 |
| sigmoid双层网络 |
0.02297293823671869 |
- 实验:对两个不同单层网络同时进行十次测试 得到结果 取平均
- 可见在拟合任务上 单层情况下 越多的神经元数量会使得拟合的更快 且更准确
- 由于是拟合问题 所以神经元过多导致的过拟合问题就不会显现
| 网络 |
3000epoch后的L1误差 |
| 32个神经元 |
0.014551067166471124 |
| 128个神经元 |
0.006307620398259217 |
实验数据存储在 Task1\img\experiencedata\data.json
实验都采取早停策略
此处都使用relu做激活函数,所以当神经元数量增加或减少时,学习率需要调整
1024 单层网络Relu
- 高的学习率任意使得网络在不断震荡难以收敛,甚至可能过快的将部分参数变为0,减缓参数的更新速率
- 更新学习率使得网络能够探索更优的解
| 网络 |
图 |
| lr = 0.0001 |
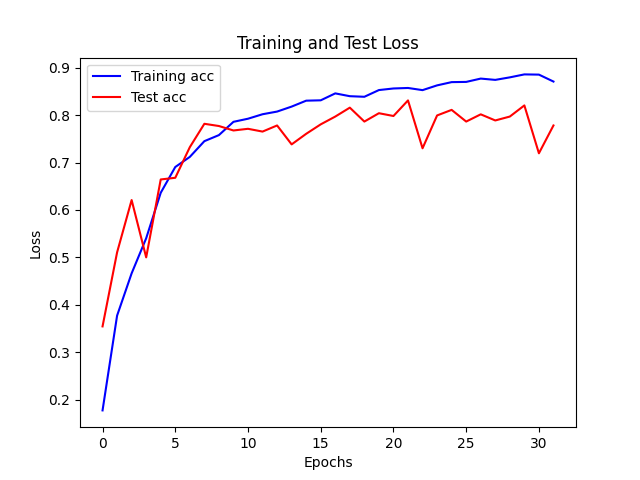 |
| lr = 0.001 |
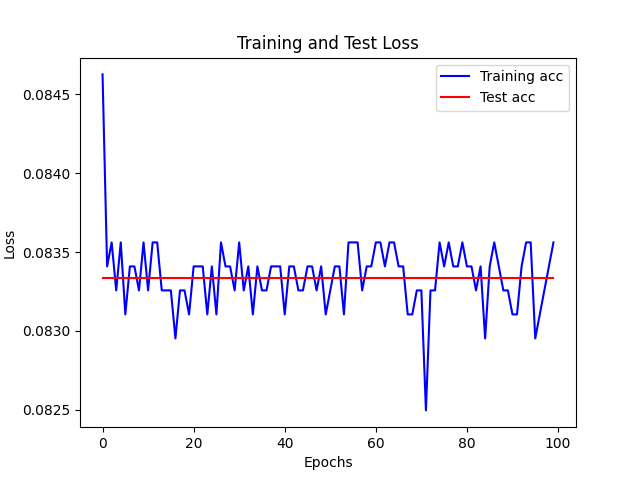 |
| lr = 0.0001 会更新学习率 |
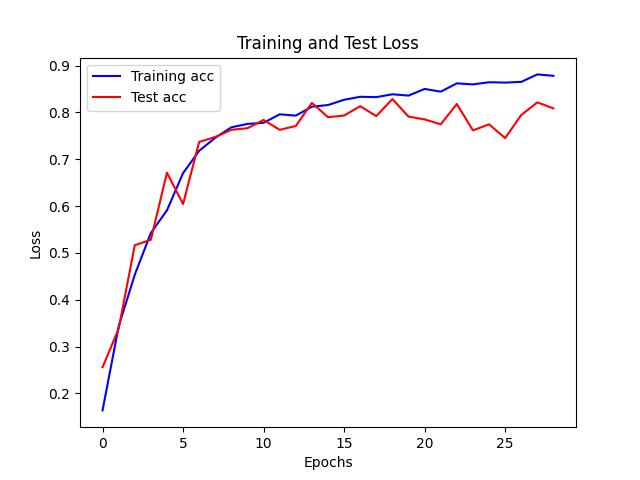 |
| 网络 |
图 |
| lamda=0 |
 |
| lamda = 0.00001 |
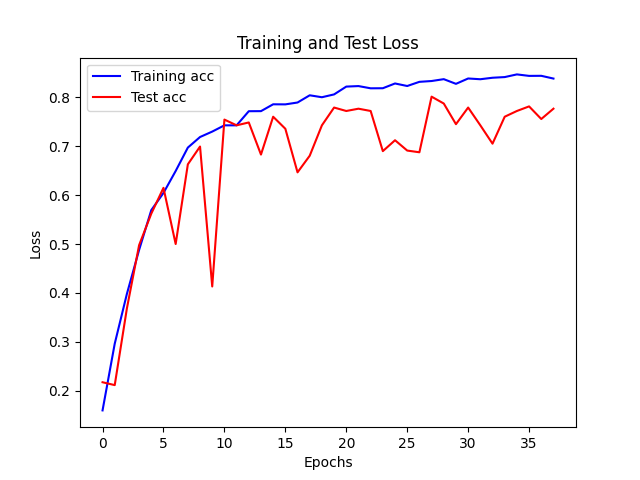 |
- 实验:对两个不同网络同时进行测试 得到结果
- 可见单层网络收敛速度较快
- 双层网络更容易不收敛
- 此处引入早停的技术
- 单层网络在30epoch内 未调整学习率 任意过早的早停
- 双层网络则是在震荡
- 说明复杂任务中,更需要较为合适的参数
| 网络 |
图像 |
| relu 1024单层网络 |
 |
| relu 1024-512 双层网络 |
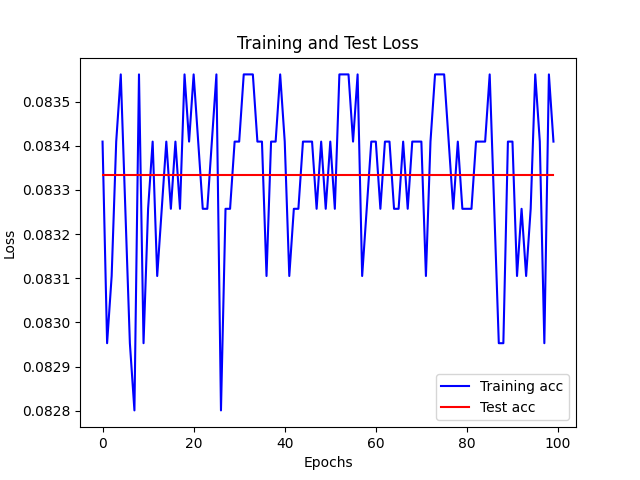 |
- 过多易过拟合,过少难拟合
- 1024个神经元较容易拟合,而512个神经元则容易欠拟合,到一定程度就开始震荡,过早收敛
| 网络 |
图像 |
| relu 1024单层网络 |
 |
| relu 512 单层网络 |
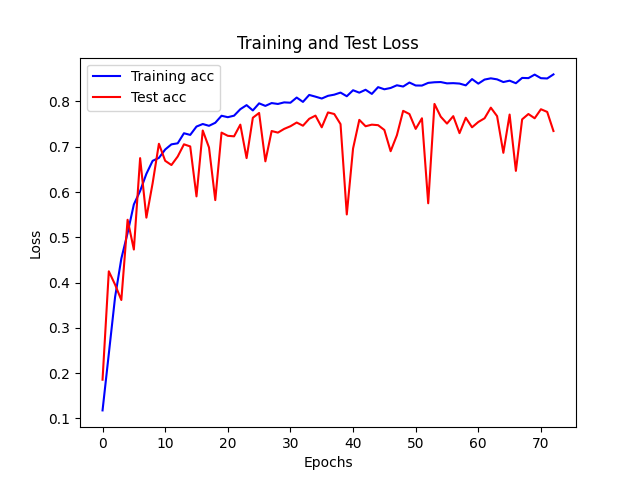 |
- 初始化参数,极大的影响了网络的拟合速度和可行性
- 在使用relu时如果参数值过大,极容易发生溢出的情况,使得网络难以训练
- 而合适的参数能够使得初始的位置比较好,可以快速拟合
- 学习率与网络结构以及激活函数都相关
- 对网络结构,越大的网络,初始学习率越小
- 对激活函数,relu激活函数所需的学习率较小,若太大易溢出;sigmoid需要的较大,太小的话参数更新速度慢
- 正则化是用来惩罚过大的参数变化的,避免参数直接转变到不好的状态,使得网络难以调整












