title	emoji	colorFrom	colorTo	sdk	sdk_version	app_file	pinned	tags	description
MASE	🤗	blue	red	gradio	3.19.1	app.py	false	evaluate metric	Mean Absolute Scaled Error (MASE) is the mean absolute error of the forecast values, divided by the mean absolute error of the in-sample one-step naive forecast on the training set.

Metric Card for MASE

Metric Description

Mean Absolute Scaled Error (MASE) is the mean absolute error of the forecast values, divided by the mean absolute error of the in-sample one-step naive forecast. For prediction 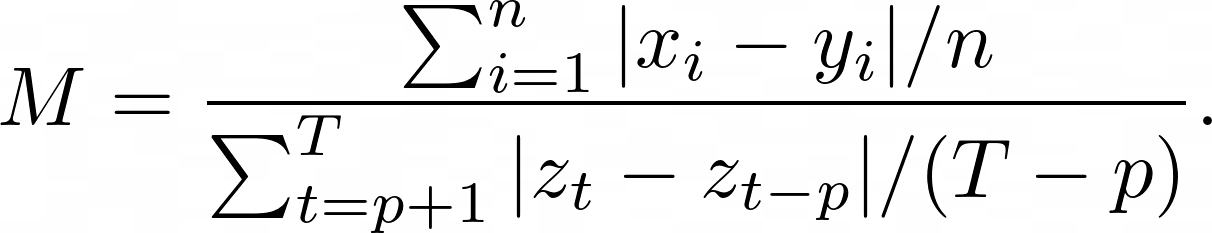$x_i$ and corresponding ground truth $y_i$ as well as training data $z_t$ with seasonality $p$ the metric is given by:

This metric is:

• independent of the scale of the data;
• has predictable behavior when predicted/ground-truth data is near zero;
• symmetric;
• interpretable, as values greater than one indicate that in-sample one-step forecasts from the naïve method perform better than the forecast values under consideration.

How to Use

At minimum, this metric requires predictions, references and training data as inputs.

>>> mase_metric = evaluate.load("mase")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> training = [5, 0.5, 4, 6, 3, 5, 2]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)

Inputs

Mandatory inputs:

• predictions: numeric array-like of shape (n_samples,) or (n_samples, n_outputs), representing the estimated target values.
• references: numeric array-like of shape (n_samples,) or (n_samples, n_outputs), representing the ground truth (correct) target values.
• training: numeric array-like of shape (n_train_samples,) or (n_train_samples, n_outputs), representing the in sample training data.

Optional arguments:

• periodicity: the seasonal periodicity of training data. The default is 1.
• sample_weight: numeric array-like of shape (n_samples,) representing sample weights. The default is None.
• multioutput: raw_values, uniform_average or numeric array-like of shape (n_outputs,), which defines the aggregation of multiple output values. The default value is uniform_average.
  • raw_values returns a full set of errors in case of multioutput input.
  • uniform_average means that the errors of all outputs are averaged with uniform weight.
  • the array-like value defines weights used to average errors.

Output Values

This metric outputs a dictionary, containing the mean absolute error score, which is of type:

• float: if multioutput is uniform_average or an ndarray of weights, then the weighted average of all output errors is returned.
• numeric array-like of shape (n_outputs,): if multioutput is raw_values, then the score is returned for each output separately.

Each MASE float value ranges from 0.0 to 1.0, with the best value being 0.0.

Output Example(s):

{'mase': 0.5}

If multioutput="raw_values":

{'mase': array([0.5, 1. ])}

Values from Popular Papers

Examples

Example with the uniform_average config:

>>> mase_metric = evaluate.load("mase")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> training = [5, 0.5, 4, 6, 3, 5, 2]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)
>>> print(results)
{'mase': 0.1833...}

Example with multi-dimensional lists, and the raw_values config:

>>> mase_metric = evaluate.load("mase", "multilist")
>>> predictions = [[0.5, 1], [-1, 1], [7, -6]]
>>> references = [[0.1, 2], [-1, 2], [8, -5]]
>>> training = [[0.5, 1], [-1, 1], [7, -6]]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)
>>> print(results)
{'mase': 0.1818...}
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training, multioutput='raw_values')
>>> print(results)
{'mase': array([0.1052..., 0.2857...])}

Limitations and Bias

Citation(s)

@article{HYNDMAN2006679,
    title = {Another look at measures of forecast accuracy},
    journal = {International Journal of Forecasting},
    volume = {22},
    number = {4},
    pages = {679--688},
    year = {2006},
    issn = {0169-2070},
    doi = {https://doi.org/10.1016/j.ijforecast.2006.03.001},
    url = {https://www.sciencedirect.com/science/article/pii/S0169207006000239},
    author = {Rob J. Hyndman and Anne B. Koehler},
}

Further References

• Mean absolute scaled error - Wikipedia