Victor Maia, John Burnham, Maisa Milena
Abstract. We present the design of a minimal, decentralized operating system called Moonad which aims to solve many problems with existing computer architectures and programming languages. Instead of assembly, Moonad's low-level machine language is based on a massively parallel graph-reduction system called interaction nets, with an accompanying new hardware architecture. Moonad's high-level language is a dependently typed programming language called Formality which can use the Curry-Howard-Lambek isomorphism to state and prove mathematical theorems about its own programs. Instead of the usual package manager or app-store, software is distributed via a type-indexed repository of algorithms, applications and theorems. A distributed file system, self-sovereign identity and smart-contract platform are built-in via Phos, an Ethereum fork which replaces the Ethereum Virtual Machine with the Formality-Core Virtual Machine (FVM).
- Why?
- Formality-Core
- Formality
- Moonad
- Phos
Moonad comes from the realization that our computers, operating systems, programming languages and package managers are flawed and primitive. Computer science has had tremendous breakthroughs over the past several decades, most of which are barely used in practice. For every software-related fiasco news you see, there is often an existing technology capable of preventing it trivially, yet we still struggle with those problems in a daily basis. Moonad aims to bring all those insights into a real product that "just works", in the form of a new, modern operating system. Here are just a few examples of some serious, yet solveable problems with existing technology:
From a security perspective, we had a single, small malicious package cause the entire web ecosystem to collapse, twice. We have been dealing with SQL and JavaScript injections since the birth of the internet. It has been 2k years since the first mathematical proof was published, yet we still lose absurd amounts of money for bugs like the heartbleed and TheDAO. One example may have degraded Planet Earth's total installed CPU capacity by 30%. Faulty software and malwares are widespread on the industry, sometimes causing airplanes to crash, and hospitals to stop operating.
Imagine a world without bugs and malware? As far-fetched as it might seems, existing technologies such as formal proofs are perfectly capable of eliminating bugs by ensuring that a program's behavior matches its specification1. Here, we will explain how Moonad, an operating system built on top of a proof language can address these problems.
From a performance perspective, our most widely used programming languages
have several, unavoidable inefficiencies that, by design, make them many times
slower than they ought to be. Our CPUs are built using sequential models of
computation that have hit a bottleneck and stagnated. The recent rise of GPUs
for high-performance computing doesn't fully solve this problem because the way
we're used to build software still relies profoundly on sequential idioms such
as for-loops. Even if our languages were more GPU-friendly, the necessity for
ASICs in applications such as crypto-currency mining shows that even GPUs are
still not making perfect use of the underlying computing capabilities of our
physical world. Imagine if we had processors for arbitrary programs that
couldn't be subsumed by ASICs? Imagine if our programming languages could
compute optimally in parallel without any programmer effort? Here, we will
propose a general-purpose, massively parallel computer architecture that is
almost optimal up to the laws of physics, in a sense that will be made precise
later on, as well as detail how future programming languages can be designed to
make the best use of those capacities.
From a productivity perspective, we are extremelly inefficient. When it
comes to features, our programming languages lag behind theory. Java took
decades to implement lambdas. JavaScript took years to figure out monads (and
failed). Modern languages such as Go struggle with aspects as simple as
polymorphic datatypes. On top of that, we never wasted as much developer time.
By searching, for example, "def mergesort" filetype:py we get 454 results: hundreds of re-implementations of
the same particular function, in the same particular language; and chances are
this number is hugely underestimated. Imagine if all that effort was spent
somewhere else? Our developers could be creating new technology, researching
space travel, solving climate change, curing cancer, yet they are, almost
without exception, reinventing the wheel. Here, we will explain how several
type-theory insights can lead us to unprecedented developer productivity gains.
Note that this kind of unproductivity doesn't affect only developers. Mathematical publishing is in an even worse state. In the apex of the computing era, findings and publications are still communicated through primitive, computer-inaccessible, text-based languages. Once you realize proofs are just code, the entire academic system becomes a huge, inefficient, paid package manager. Citations can be seen as manual imports and peer-reviewing is just an error-prone, human-laborious type-checker. Errors in earlier works propagate upwards, paywalls make knowledge private. The entire system extremely fragile, bureaucratic and inefficient. By building an operating system on top of a proof language, the same ideas that improve developer productivity also apply to mathematics as a whole, leading to an unprecedented leap in scientific progress.
Finally, Moonad has many other minor aspects that set it apart from existing operating systems. For example, instead of local files, it uses decentralized storages (similar to IPFS and Swarm). This means that, whenever you save a file locally, it is backed up, encrypted, in a network of computers. This has many consequences. For one, there isn't such a thing as "local files" anymore: once you save a file, you're able to access it from anywhere. If your hardware is damaged, nothing is lost. Backups become obsolete. Sharing a file or a photo with someone becomes as easy as sending its path. This also has means that publishing a site is straightforward: all you have to do is make its directory public. Naturally, DDOSes also become a thing of the past.
Moonad also comes with the Phos blockchain (an Ethereum fork) built-in. This has many consequences. For example, instead of local users, we have Phos addresses. This makes website logins and passwords obsolete, since they all can use signatures from the same crypto account. Similarly, the entire credit-card payment system is replaced by direct crypto payments. You don't need to trust a site not to misuse or steal your credentials. Credit-card disputes become a thing of the past. Blockchain's benefits go much beyound payments, though. Important business agreements can be formalized through automatically enforced smart-contracts. Virtual assets such as items in online games are allowed to have a much more real value, since there isn't a centralized company capable of "changing the rules of the game" or even turning it down. Finally, any kind of censorship in applications such as torrent websites become impossible.
Now, we will explain several components of the operating system, and elaborate on how they solve existing problems, starting at the low-level Formality-Core language and working our way upwards.
Operating systems often make a distinction between high and low-level languages. This enables a separation of concerns: while high-level languages focus on usability and user-friendliness, their low-level counterparts focus on speed and efficiency, often resembling the underlying computer architecture, which is usually be modelled by Turing machines. While that model has worked well for the last few decades, it hit a bottleneck as the speed of sequential CPUs stagnated. Meanwhile, the computing power of GPUs, FPGAs, ASICs and other parallel architectures keeps growing exponentially, but, sadly, modern programming languages can't make effective use of those advancements. Functional programming languages, which are based on alternative model, the lambda calculus have been sold as a solution, but never fulfilled its promises, partly due to the inherent complexity of beta-reduction.
In 1997, a very simple graph-rewrite system with only 3 symbols and 6 rules has been shown to be a universal model of computation 2. This system, interaction combinators, is remarkable for having the best properties of Turing machines and the lambda calculus. Like the former, it can be evaluated as a series of atomic, local operations with a clear physical implementation. Like the later, it is inherently parallel, but in a more robust manner, admitting desirable computational properties such as strong confluence, optimal sharing, zero-cost garbage-collection and so on. For those reasons, we use a slightly modified version of symmetric interaction combinators, Formality-Core as our lowest-level machine language. This allows our applications to target a computing model that is ready for the upcoming future of massively parallel architectures.
Our implementation has advantages over previous interaction net graph-reduction systems (such as the Bologna Optimal Higher-order Machine) in that it requires no book-keeping, requires only 128 bits per lambda or pair, has unboxed 32-bit integers and constant-time beta reduction. This is possible because Formality-Core is not based on classic logic, but, instead, Elementary Affine Logic. All programs written in Formality are guaranteed to halt, and enjoy key computational characteristics that differ from classic functional languages. This directly enables many of the runtime features and optimizations (such as no book-keeping) described above, although without loss of generality as Formality-Core can model Turing-Complete programs via corecursion. In other words, Turing-Complete computation can be performed by writing an iteration step function in Formality-Core and looping this function infinitely in your runtime system. We view this design decision as a principled acknowledgement that in practice no real software is Turing-Complete; actual physical systems can only be finite state machines.
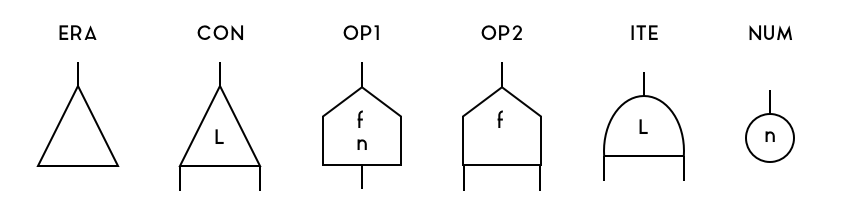
While conventional low-level languages describe they programs as a series of statements in an assembly-like language, Formality-Core programs are simply graphs of a specific format, with the following six node types:
Each node has 1 to 3 outgoing edges, called "ports", depending on the node type.
The upward-pointing port in the above diagram is called the main port, and, if
present, the one nearest to it in counter-clockwise direction is the aux1
port and the other one is the aux2 port. Additionally, some nodes can be
annotated with one or two symbolic labels (e.g. a 32-bit int).
Graph rewriting occurs when two nodes have their main ports connected to one
another, and such a structure is called a "redex" (for "reducible-expression")
or an active pair.
To describe the Formality-Core nodes from the above diagram in more detail:
- ERA: Eraser node, eliminates nodes on its
mainport - CON: Constructor node, either eliminates or duplicates nodes depending on whether its symbolic label matches its redex counterpart
- NUM: The symbolic label of this node represents a 32-bit integer.
- OP1: A unary arithmetic operation node, where the first label describes a binary arithmetic operation (such as addition or multiplication) and the second label describes the first integer argument.
- OP2: A curried binary arithmetic operation node, whose label describes and arithmetic operation and reacts with a NUM node to produce an OP1
- ITE: A numeric branching node, which reacts with a NUM node in one way if the node's numeric value is 1 or another way if the node's value is anything else.
Any fully connected arrangement of those nodes forms a valid Formality core program.
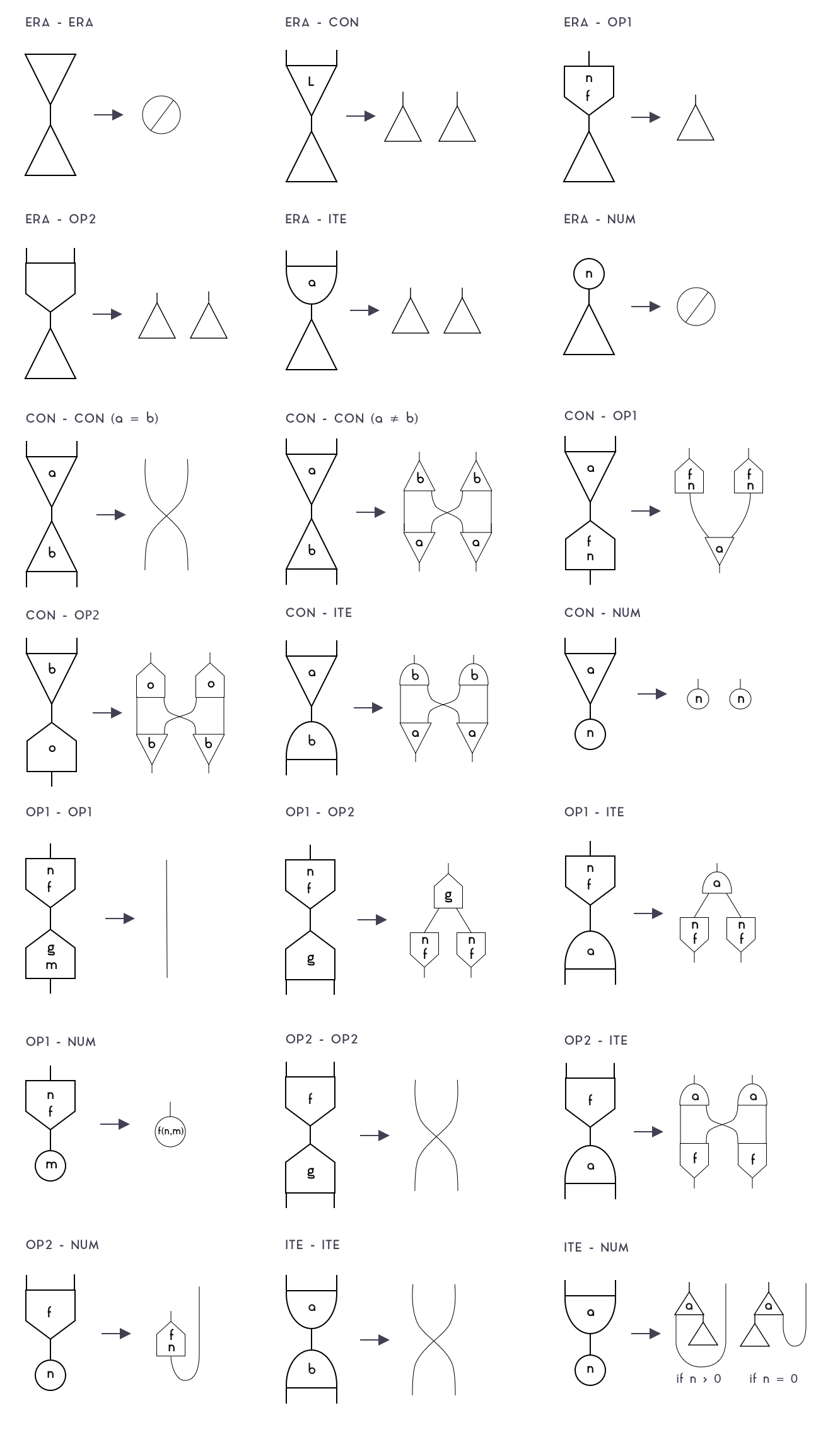
There are 21 graph rewrite rules in Formality-Core:
Those rewrite rules dictate that, whenever a sub-graph matches the left side of a rule, it must be replaced by its right side. Here is an illustration of how this works in practice:
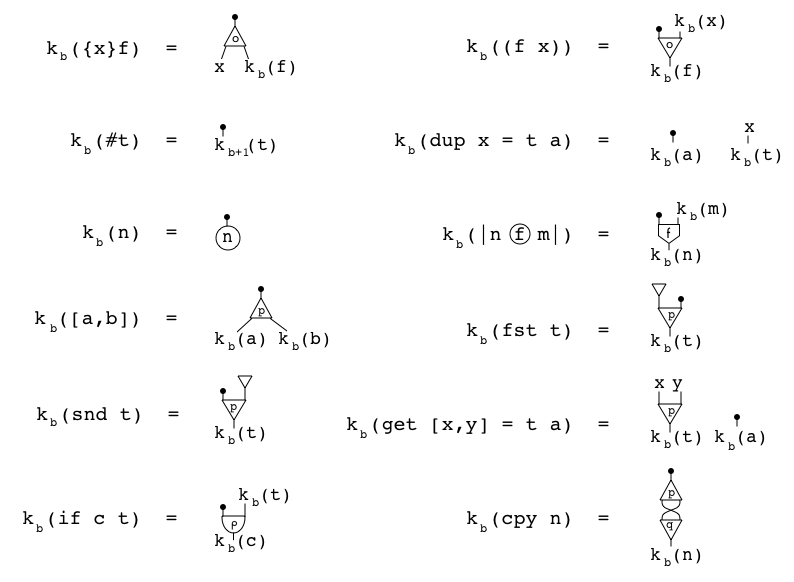
Of course, we cannot easily write software directly in the Formality-Core interaction net graph, so we have a textual representation which compiles to it. Here is a sample:
def vec_add: {a b}
get [ax,ay] = a
get [bx,by] = b
[|ax + bx|, |ay + by|]
def vec_cpy: {a}
get [ax,ay] = a
cpy ax = ax
cpy ay = ay
[[ax,ay], [ax,ay]]
def RIGHT : 0 // 1
def DOWN : 1 // 0
def LEFT : 2 // -1
def UP : 3 // 0
def dir_to_vec: {a}
cpy a = a
if |a < 2|
then:
if |a == 0|
then: [ 1, 0]
else: [ 0, 1]
else:
if |a == 2|
then: [-1, 0]
else: [ 0, -1]
And these are the compilation rules:
As unintuitive as it may seem, this simple graph-rewrite system is extremely powerful, because it captures the two fundamental rules of computation: annihilation and commutation. In fact, only the ERA and CON nodes are truly necessary in terms of expressive. The remaining nodes are including only for efficiency and convenience.
The Curry-Howard correspondence states that there is a structural congruence between computer programs and proofs in formal logic. While in theory this implies that software developers and mathematicians are engaged in substantially the same activity, in practice there are many barriers preventing the unification of the two fields. Programming languages with type systems expressive enough to take advantage of Curry-Howard, such as Haskell, Agda and Coq generally have substantial runtime overhead, which makes them challenging to use, particularly at the systems programming level. On the other hand, systems languages such as Rust, Nim or ATS, have shown that type systems can greatly enhance usability and correctness of low-level software, but either have type systems too weak to fully exploit Curry-Howard (Rust, Nim), or introduce syntactic complexity that limits adoption (ATS). In other words, there are lots of slow languages with great type systems and lots of fast languages with lousy type systems.
As programmers and as mathematicians, we don't want to compromise. On one side, mathematicians have the power of rigor: there is nothing more undeniably correct than a mathematical proof. Yet ironically, those proofs are often written, checked and reviewed by humans in an extremelly error-prone process. On the other side, programmers have the power of automation: there is nothing more capable of performing a huge set of tasks without making a single mistake than a computer program. Yet, equally ironically, most of those programs are written in an unrigorous, bug-ridden fashion. Formality lies in the intersection between both fields: it is a programming language in which developers are capable of implementing everyday algorithms and data structures, but it is also a proof language, on which mathematicians are capable of proposing and proving theorems.
TODO
TODO
TODO
Footnotes
-
Some readers might object here that while formal proofs can ensure that a program's implementation matches its specification, it cannot eliminate errors inherent to the specification. This is true, unless there is a formalizable meta-specification of the specification, in which case we can construct a proof showing consistency between the two. Otherwise, the specification of the specification is the mind of the programmer or user themselves, and in this domain there may be many bugs which are not amenable to elimination via formal methods. ↩
-
Yves Lafont, Interation Combinators, Institut de Mathematiques de Luminy, 1997 (https://pdfs.semanticscholar.org/6cfe/09aa6e5da6ce98077b7a048cb1badd78cc76.pdf) ↩