TensorBoard 直方图面板其实是在 TensorFlow 图表上显示 Tensor 的分布是如何随时间变化而变化。通过显示大量不同时间点的直方图来可视化 tensor 的变化。
一起看看一个简单例子:一个随时间变化的常分布的变量
TensorFlow 的 tf.random_normal 单元非常适用于这类问题。通常在 TensorBoard 里我们会先用一个 'tf.summary.histogram' 单元来总结数据。如果想了解此总结单元的运行机制,请看 TensorBoard 教程。
这里是段能生成直方图总结的代码,这类总结含有常分布数据而且其平均值随时间增加而增加。
import tensorflow as tf
k = tf.placeholder(tf.float32)
# 生成一个平均值会变化的常分布
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# 用直方图总结记录这个常分布
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# 建立 session 和总结写入器
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
summaries = tf.summary.merge_all()
# 建立一个循环并把总结写入硬盘
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)一旦下面代码运行,我们可以用命令行将数据导入到 TensorBoard:
tensorboard --logdir=/tmp/histogram_exampleTensorBoard 运行的时候,通过 Chrome 或者 Firefox 加载并打开直方图面板,就能看到用直方图可视化的常分布数据。
tf.summary.histogram 取一个任意大小形状的 Tensor,并把它压缩成有很多区间的直方图数据结构。例如当我们想把 [0.5, 1.1, 1.3, 2.2, 2.9, 2.99] 分配到不同区间,我门可以分三个区间:
- 一个区间包含从 0 到 1 的所有元素 (包含一个,0.5),
- 一个区间包含从 1-2 的所有元素(包含两个元素,1.1和1.3),
- 一个区间包含从 2-3 的所有元素(包含:2.2,2.9,2.99)。 TensorFlow 用一个类似的方法去生成区间,但不同的是,它不只生成几个区间,而是为大而分散的数据集生成数千个区间。取而代之的是指数分布的区间,大部分靠近0,相对少部分靠近大的数字。 然而,视像化指数分布的区间比较棘手;如果高度用来表示个数,宽一点的区间面积就较大,即使其包含的元素个数一样。相反如果用面积来表示个数,就无法对高度做对比。因而,TensorFlow 的直方图对数据作 重新取样 并分配到等宽的区间。这也不是完美的方案。
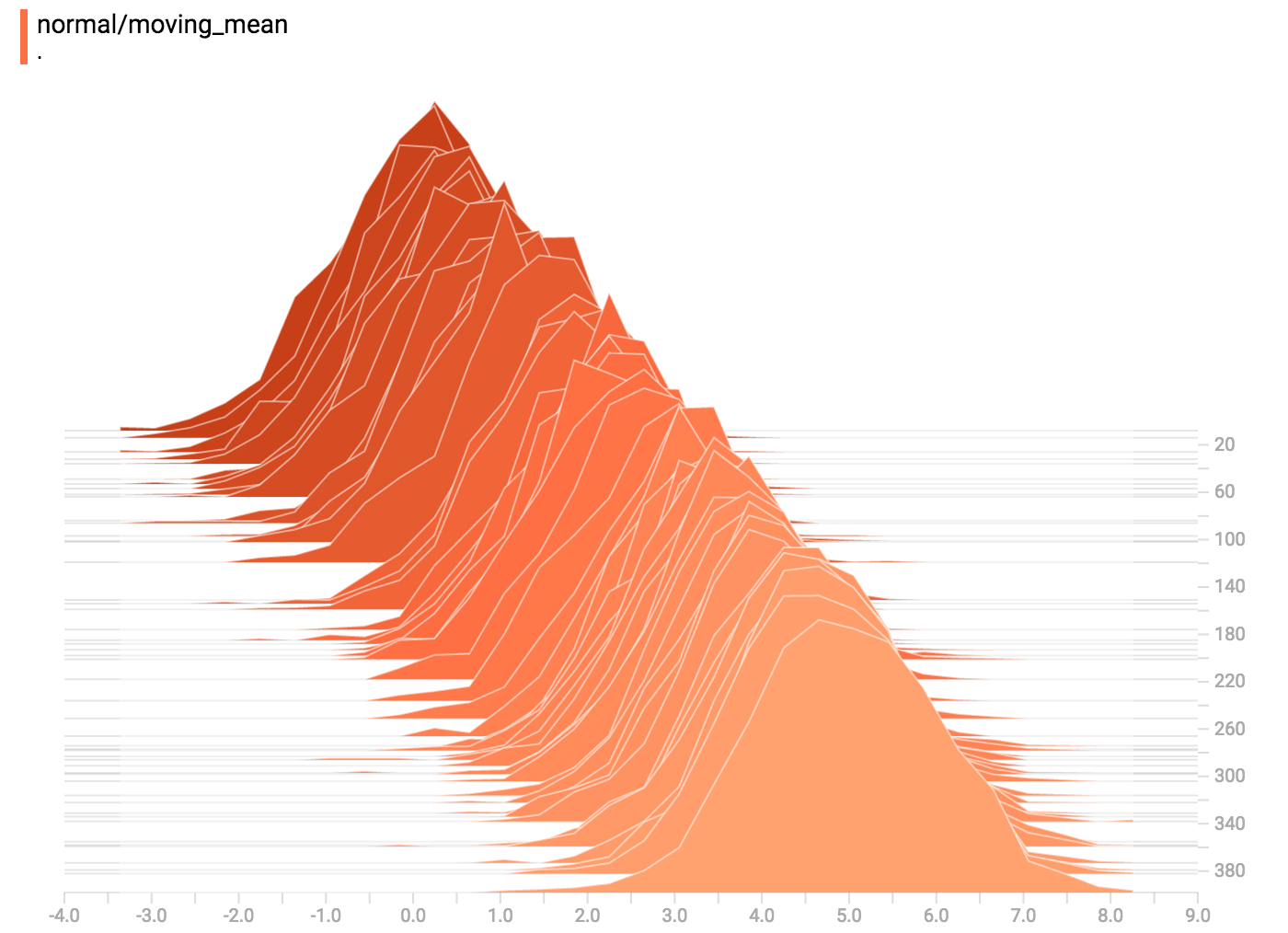
直方图视化器里面的每一截面代表一个直方图。这些截面根据步骤来整理:旧的截面(例如步骤0)会放得比较“靠后”而且颜色较深,而较新的截面(例如步骤400)放得靠前而且颜色较浅。右方的 y 轴代表步骤的号码。
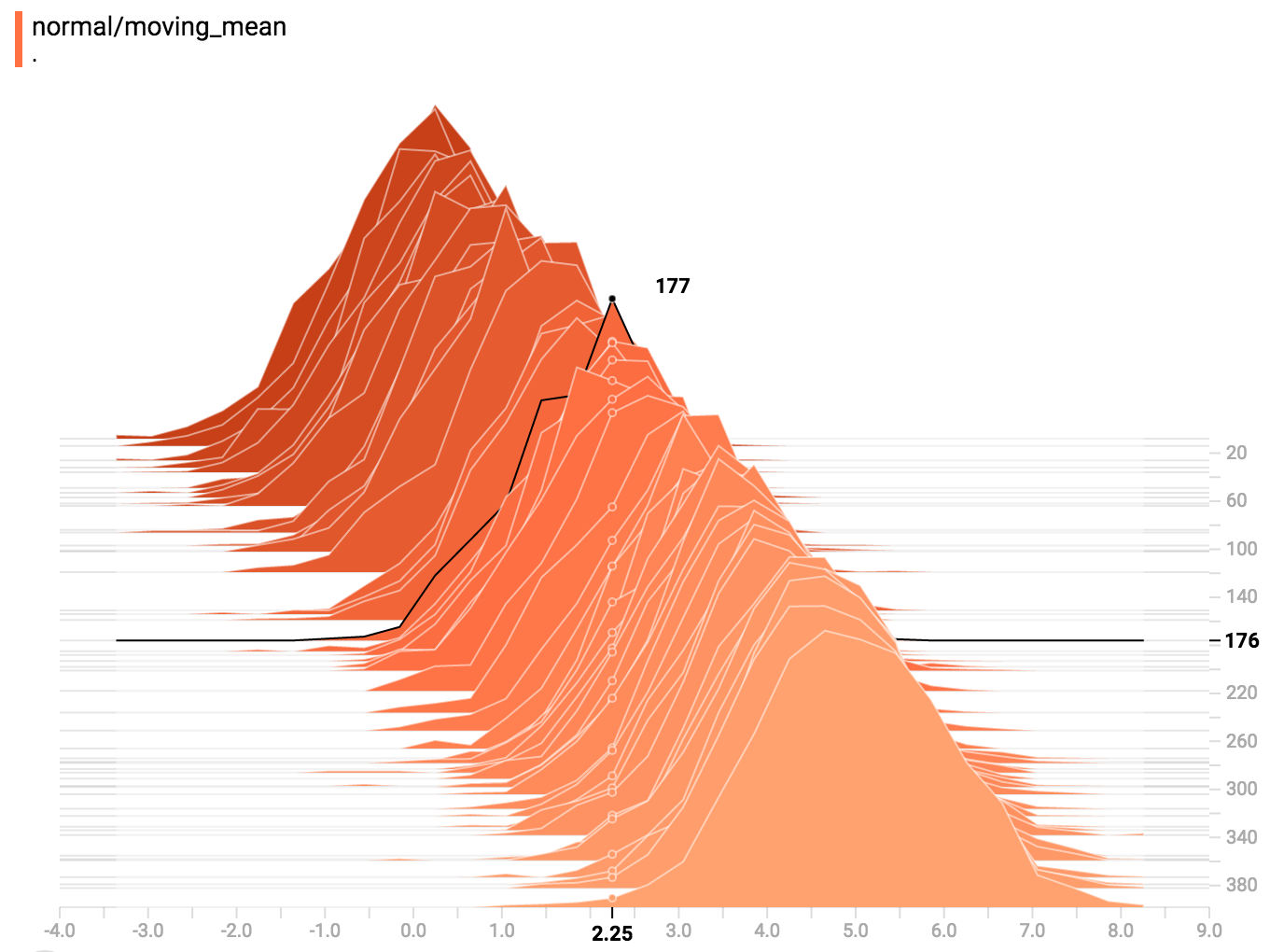
你可以把鼠标移到直方图上查看更多具体信息。例如从下方的图表我们看到在时间点 176 有个以 2.25 为中心的区间里面有 177 个元素。
此外,你还要注意一下直方图截面在单位时间或个数上不一定是均匀分布的。这是因为 TensorBoard 用 水塘抽样 来保留所有直方图的子集以达到节省内存的目的。水塘抽样保证每个样本被抽到的可能性是一样的,但因为这是随机化的算法,抽到的样品不在偶数 steps 上。
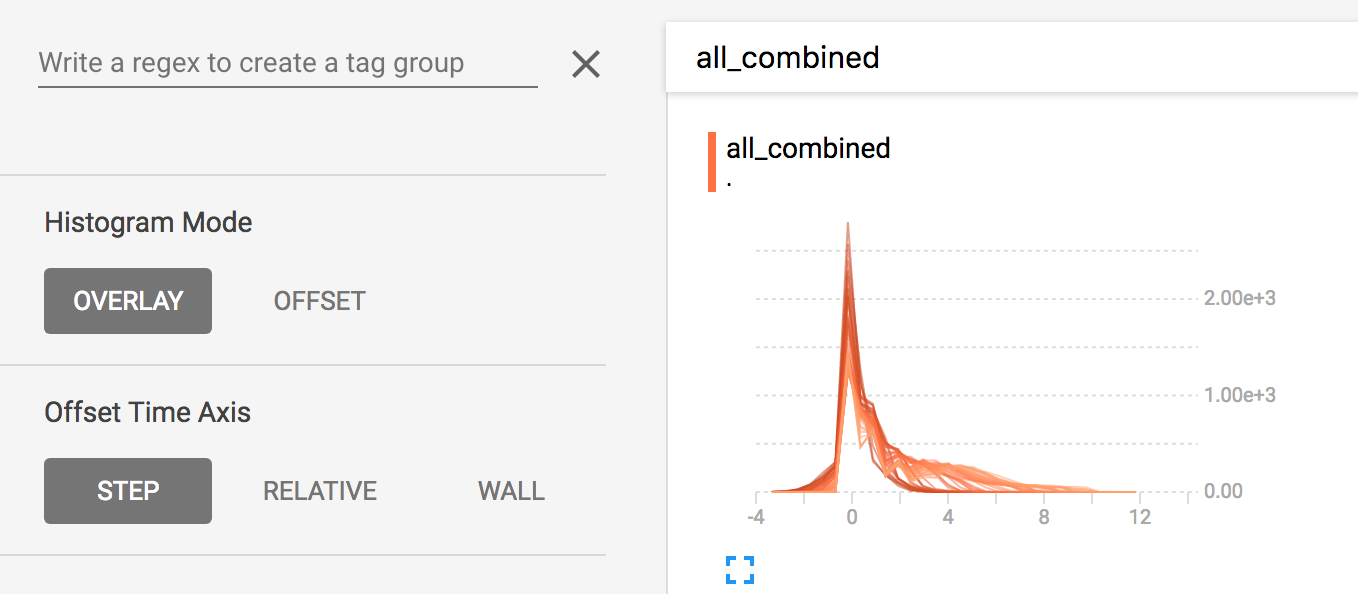
左边的选项里允许你从“并列模式”转换到“覆盖模式”:
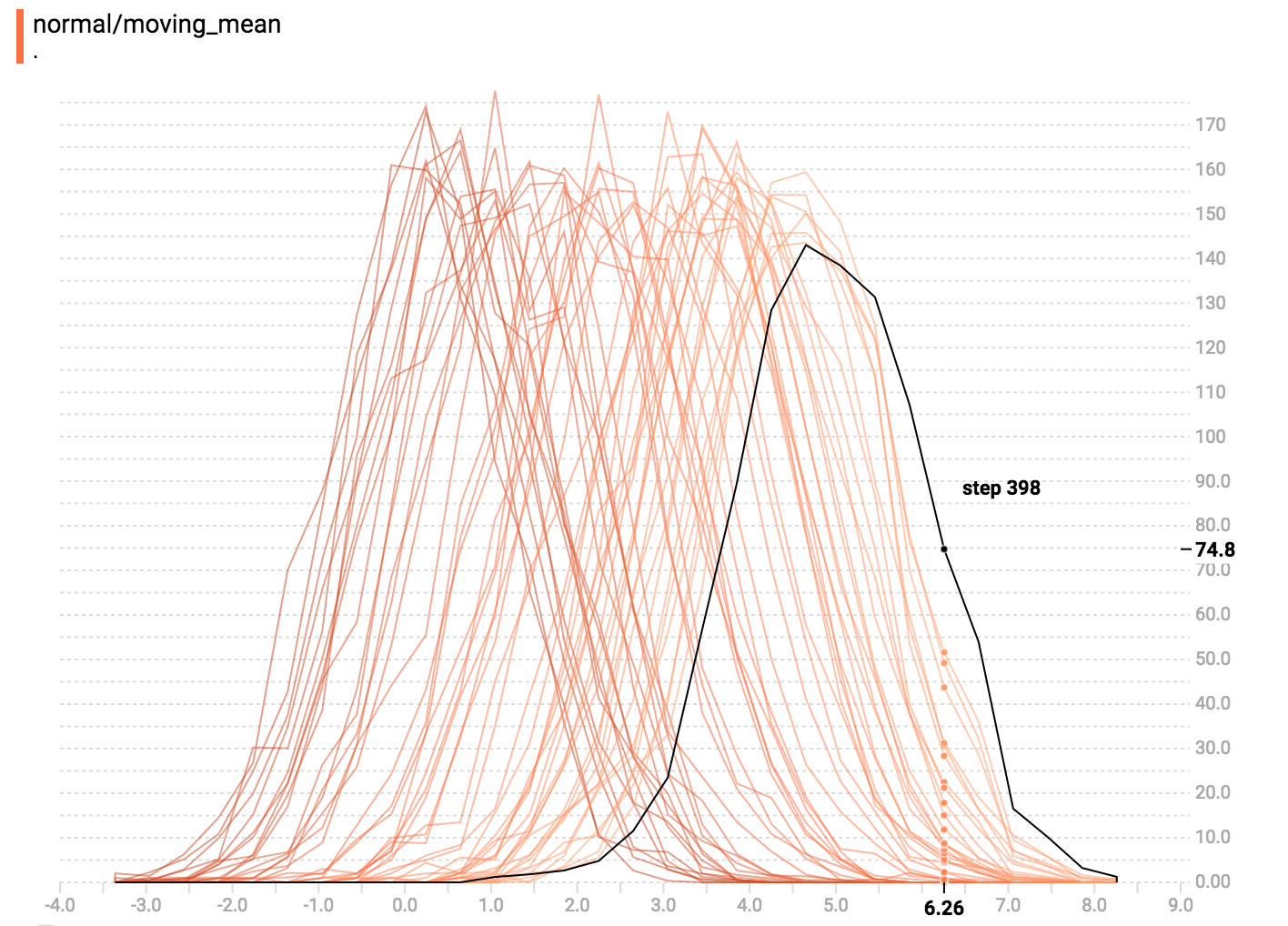
其实就是在“并列模式”里,把视觉效果转 45 度角使每个直方图截面不在时间轴上分开而都在相同 y 轴上显示。
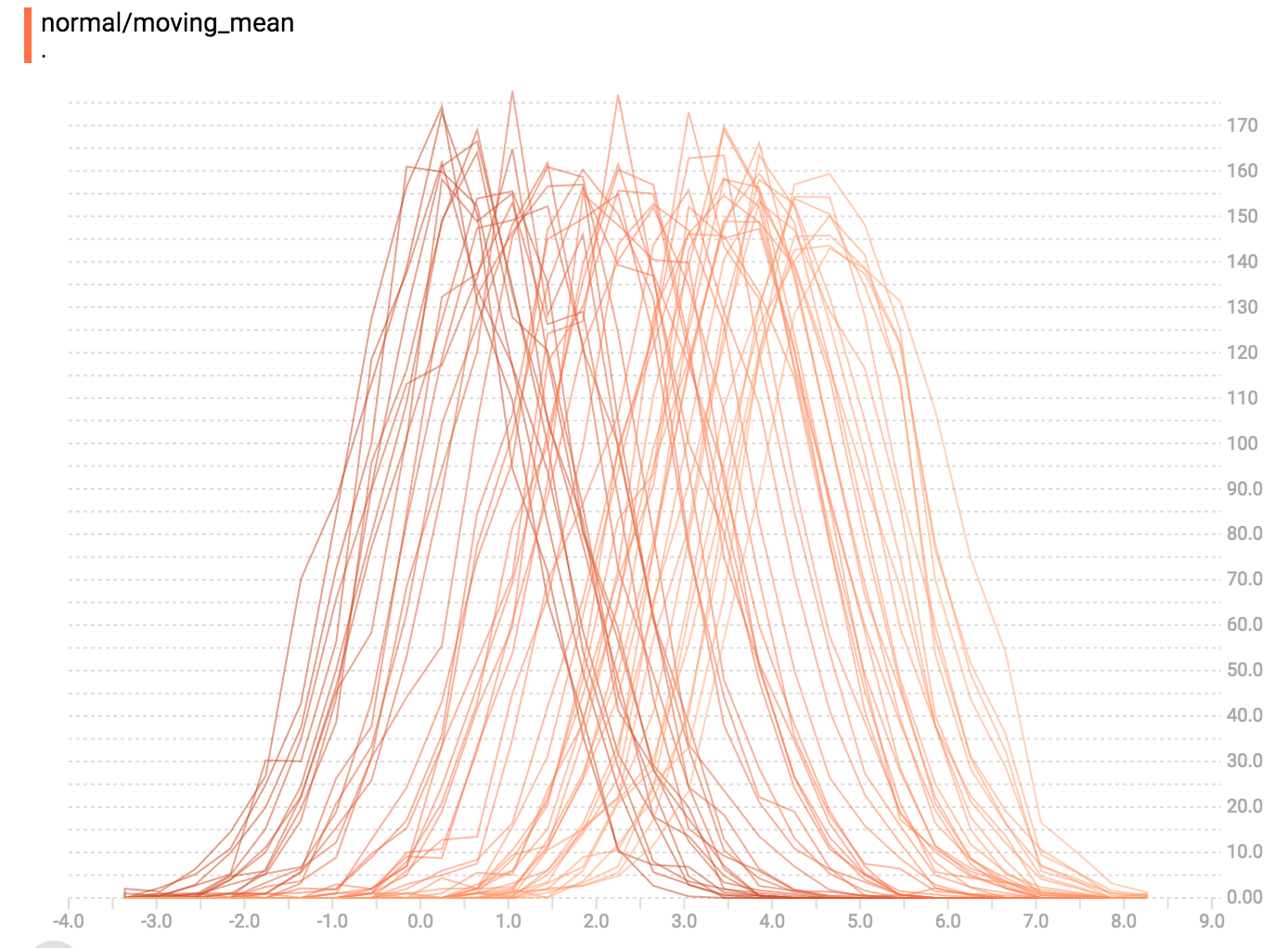
一般来说,如果你想直接比较不同直方图的个数,用覆盖模式的视觉化图表会比较好。
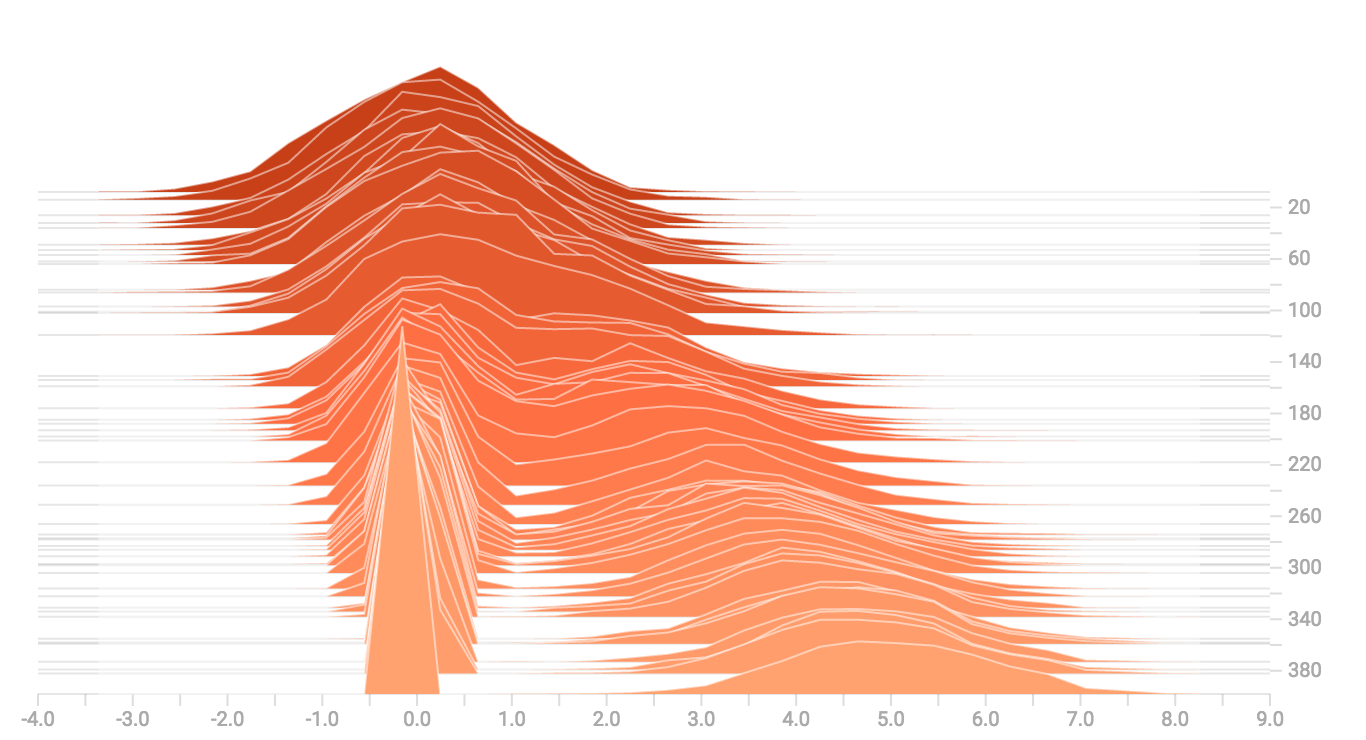
直方图面板很善于视像化多模分布。如果我们通过连结两个不同的常分布来建立一个双模分布,其代码如下:
import tensorflow as tf
k = tf.placeholder(tf.float32)
# 生成一个平均值会变化的常分布
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# 用直方图总结记录这个常分布
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# 生成一个方差会变小的常分布
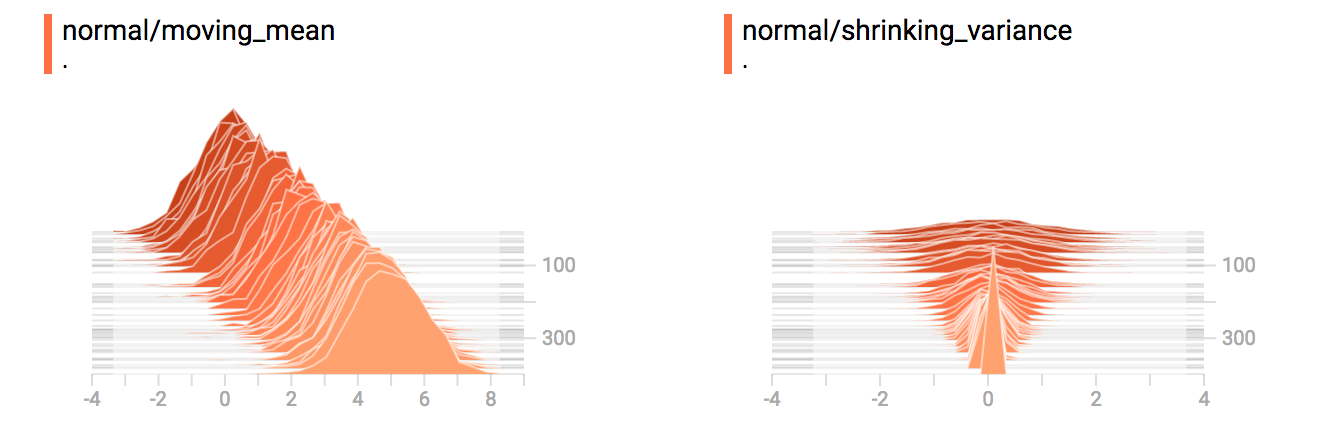
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# 同样记录其分布
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)
# 让我们整合两个分布到一组数据
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# 我们加上另一个直方图总结记录这个整合的分布
tf.summary.histogram("normal/bimodal", normal_combined)
summaries = tf.summary.merge_all()
# 建立 session 和总结写入器
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
# 建立一个循环并把总结写入硬盘
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)你已经记得我们上面例子的“变化均值”的常分布。现在我们还要一个“缩小方差”的分布。整合一起的效果图如下:
我们再试试生成并图像化更多不同的分布,然后把他们整合到一个图中。这里是我们会用到的代码:
import tensorflow as tf
k = tf.placeholder(tf.float32)
# 生成一个平均值会变化的常分布
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# 用直方图总结记录这个常分布
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# 生成一个方差会变小的常分布
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# 同样记录其分布
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)
# 让我们整合两个分布到一组数据
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# 我们加上另一个直方图总结记录这个整合的分布
tf.summary.histogram("normal/bimodal", normal_combined)
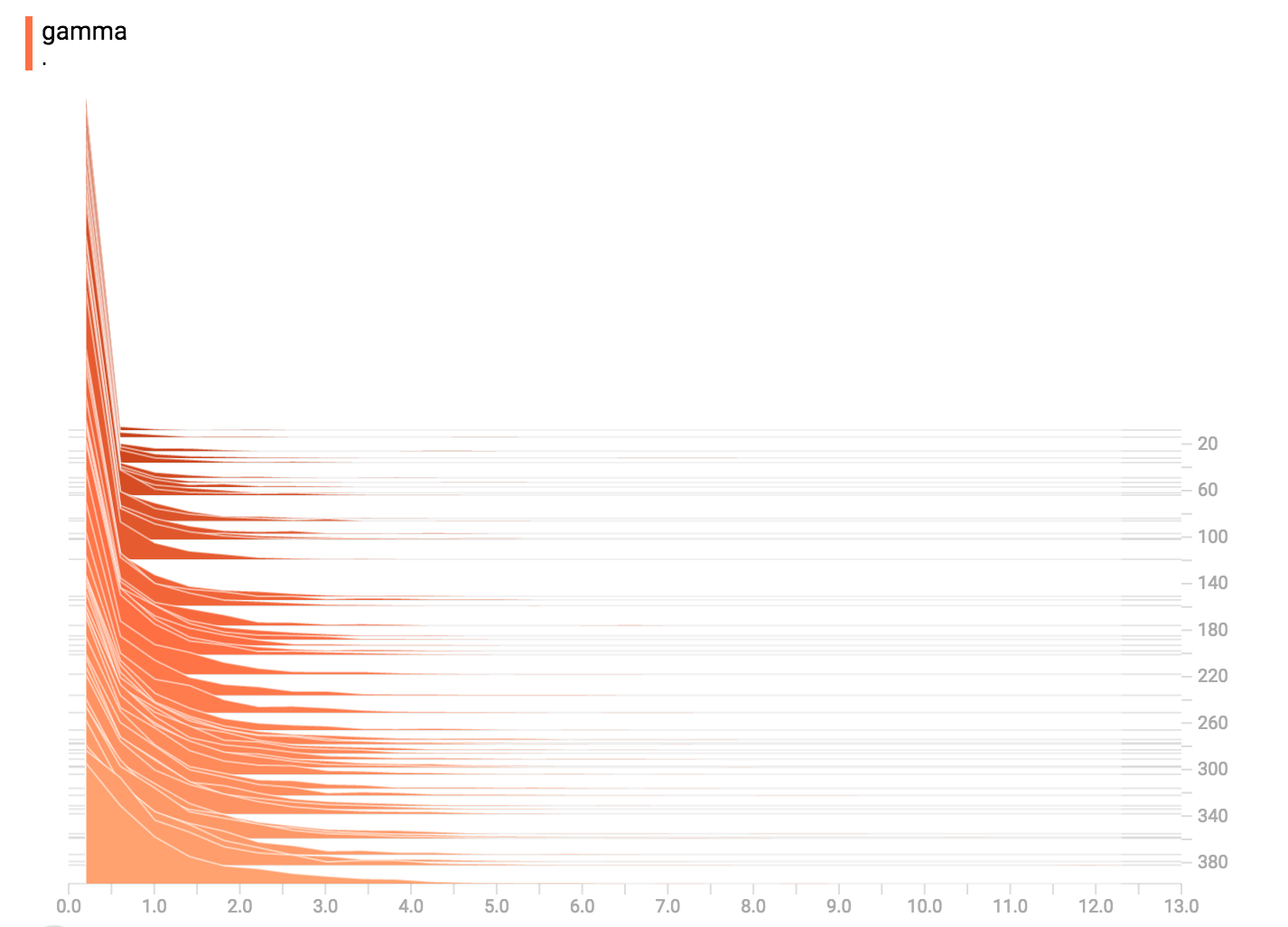
# 添加一个伽马分布
gamma = tf.random_gamma(shape=[1000], alpha=k)
tf.summary.histogram("gamma", gamma)
# 添加一个泊松分布
poisson = tf.random_poisson(shape=[1000], lam=k)
tf.summary.histogram("poisson", poisson)
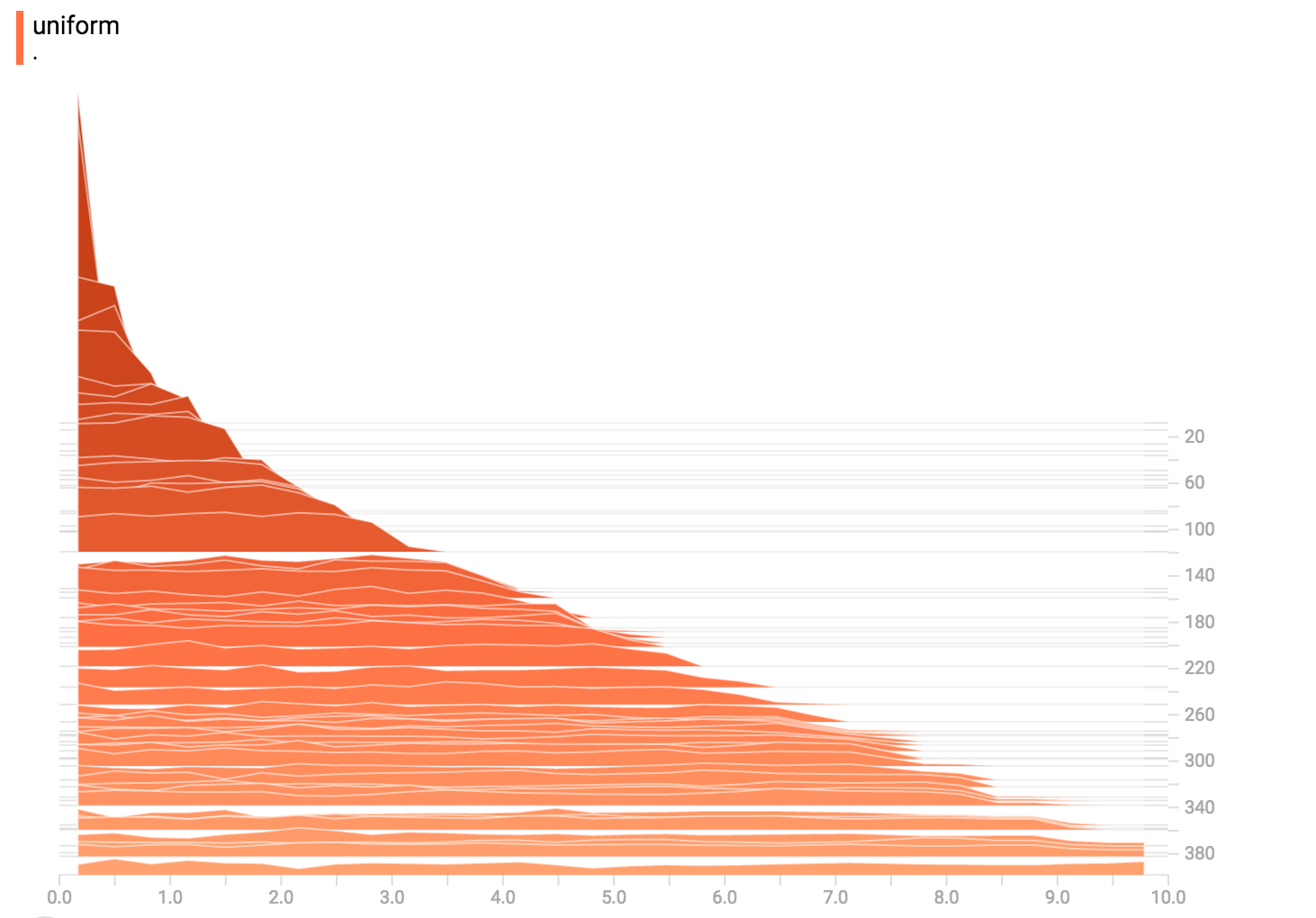
# 添加一个均匀分布
uniform = tf.random_uniform(shape=[1000], maxval=k*10)
tf.summary.histogram("uniform", uniform)
# 最后把所有分布整合到一起!
all_distributions = [mean_moving_normal, variance_shrinking_normal,
gamma, poisson, uniform]
all_combined = tf.concat(all_distributions, 0)
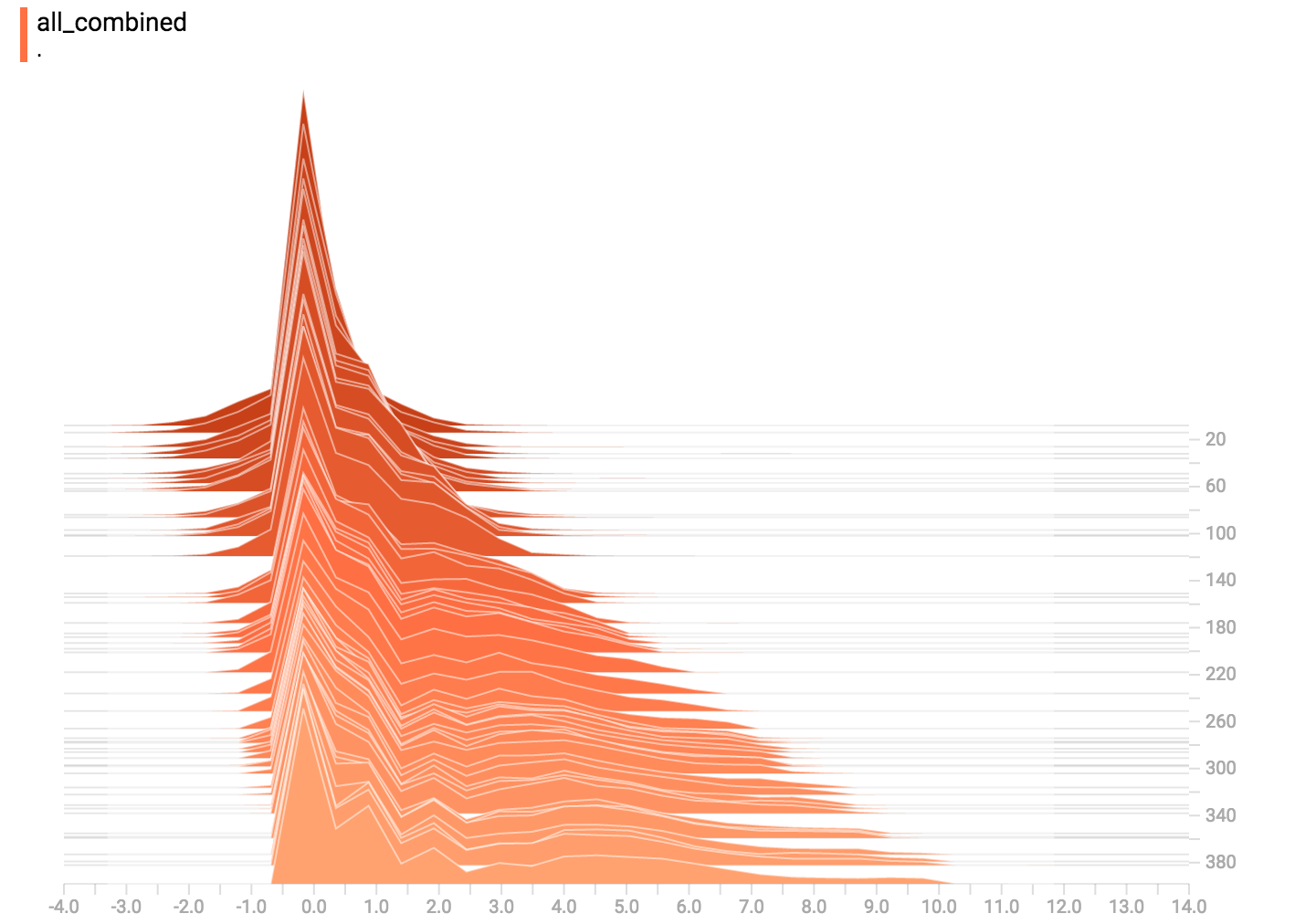
tf.summary.histogram("all_combined", all_combined)
summaries = tf.summary.merge_all()
# 建立 session 和总结写入器
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
# 建立一个循环并把总结写入硬盘
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)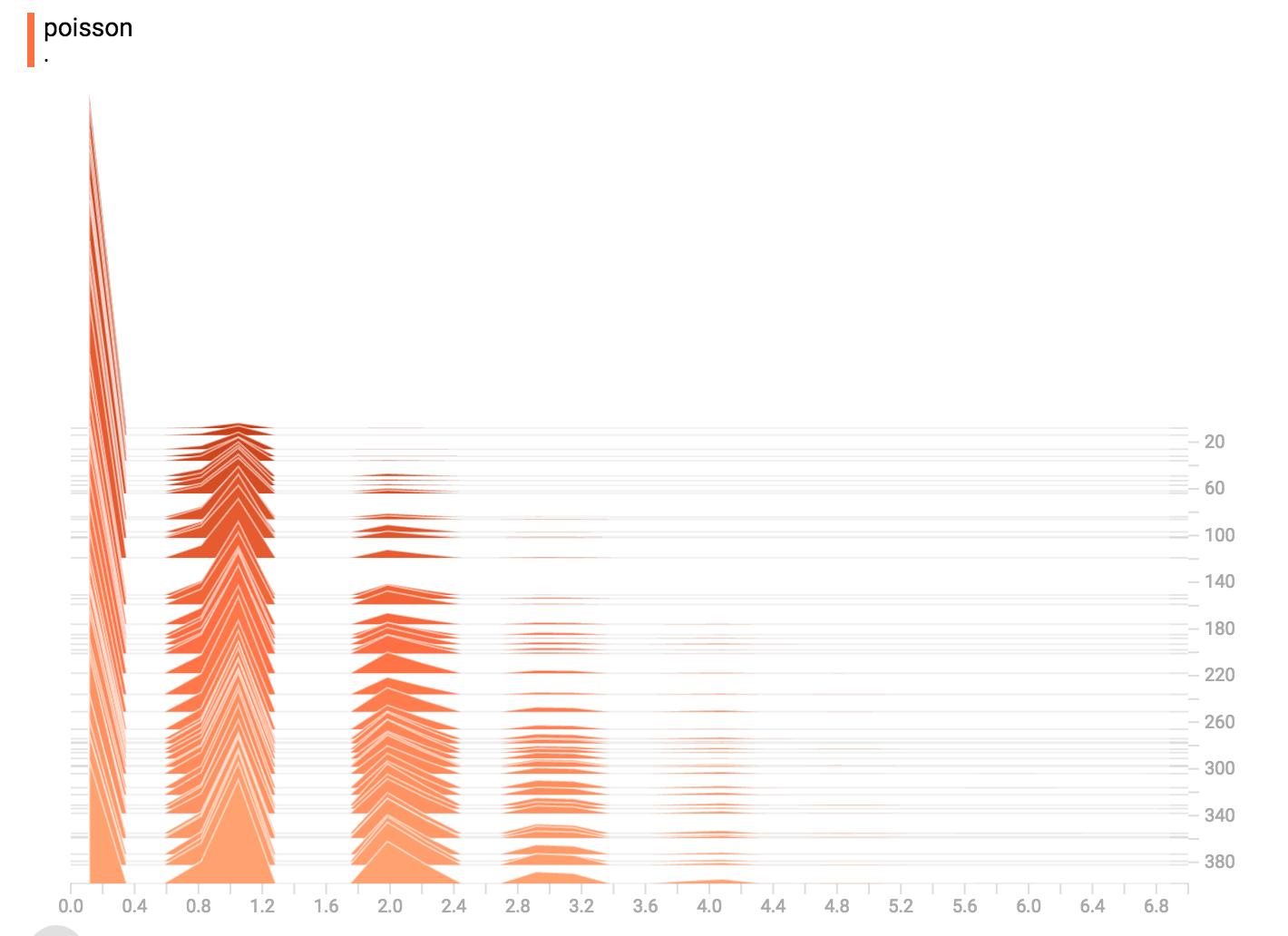
最后,我们可以把数据连接到一个形状奇特的曲线图。