tinyik

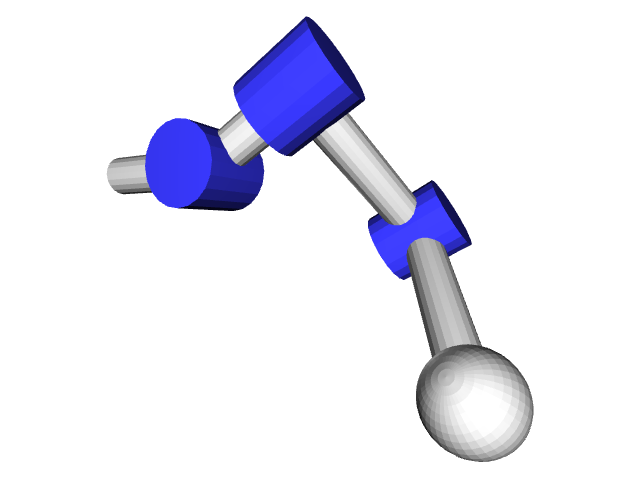
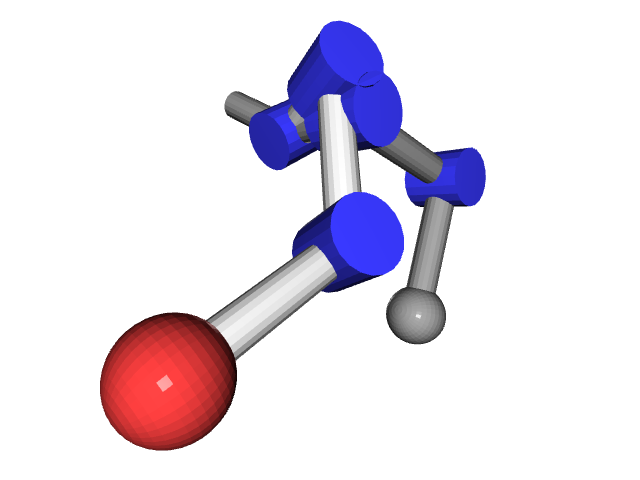
tinyik is a simple and naive inverse kinematics solver.

It defines the actuator as a set of links and revolute joints from an origin. Here is the example of a robot arm that consists of two joints that rotate around z-axis and two links of 1.0 length along x-axis:

>>> import tinyik
>>> arm = tinyik.Actuator(['z', [1., 0., 0.], 'z', [1., 0., 0.]])

Since the joint angles are zero by default, the end-effector position is at (2.0, 0, 0):

>>> arm.angles
array([ 0.,  0.])
>>> arm.ee
array([ 2.,  0.,  0.])

Sets the joint angles to 30 and 60 degrees to calculate a new position of the end-effector:

>>> import numpy as np
>>> arm.angles = [np.pi / 6, np.pi / 3]  # or np.deg2rad([30, 60])
>>> arm.ee
array([ 0.8660254,  1.5      ,  0.       ])

Sets a position of the end-effector to calculate the joint angles:

>>> arm.ee = [2 / np.sqrt(2), 2 / np.sqrt(2), 0.]
>>> arm.angles
array([  7.85398147e-01,   3.23715739e-08])
>>> np.round(np.rad2deg(arm.angles))
array([ 45.,   0.])

Optionally, it has the visualization feature. Passes the actuator to it to visualize its structure:

>>> leg = tinyik.Actuator([[.3, .0, .0], 'z', [.3, .0, .0], 'x', [.0, -.5, .0], 'x', [.0, -.5, .0]])
>>> leg.angles = np.deg2rad([30, 45, -90])
>>> tinyik.visualize(leg)

Passes with the target position, can compare before and after the IK. The gray links are before IK and the white links are after it. The red sphere is the target position:

>>> tinyik.visualize(leg, target=[.8, .0, .8])

Installation

$ pip install tinyik

With the visualization feature:

$ pip install tinyik[viz]