提升方法

笔记摘要

• 在PAC（概率近似正确(PAC, Probably approximately correct)）学习框架下，一个概念是强可学习的充分必要条件是这个概念是弱可学习的。
• 提升方法的两个问题

1. 在每一轮如何改变训练数据的权值或概率分布
2. 如何将弱分类器组合成一个强分类器

• Adaboost的解决方案：

3. 提高那些被前一轮弱分类器错误分类样本的权值，降低那些被正确分类的样本的权值
4. 加权多数表决的方法，加大分类误差率小的弱分类器的权值，减小分类误差率大的弱分类器的权值

AdaBoost算法

• 输入：弱学习算法和训练数据集 $T={(x_1,y_1), (x_2,y_2),...,(x_N,y_N)}, x\in X \subseteq R^n$
• 输出：最终分类器$G(x)$
• 步骤

1. 初始化训练数据的权值分布 $D_1=(w_{11},\cdots,w_{1i},\cdots,w_{1N},w_{1i}=\frac{1}{N})​$
2. m = 1,2, $\cdots$,M ( a ) 使用具有权值分布$D_m$的训练数据集学习，得到基本的分类器 $$G_m(x):X→{-1,+1}$$ ( b ) 计算$G_m(x)$在训练集上的分类误差率
   $$e_m=\sum_{i=1}^{N}P(G_m(x_i)\not= y_i)=\sum_{i=1}^{N}w_{mi}I(G_m(x_i)\not=y_i)$$ ( c ) 计算$G_m(x)$的系数 $$\alpha_m=\frac{1}{2}log\frac{1-e_m}{e_m}$$ ( d ) 更新训练数据集的权值分布 $$w_{m+1,i}=\frac{w_{mi}}{Z_m}exp(-\alpha_my_iG_m(x_i))​$$ $$Z_m=\sum_{i=1}^Nw_{mi}exp(-\alpha_my_iG_m(x_i))$$
3. $f(x)=\sum_{m=1}^M\alpha_mG_m(x)$
4. 最终分类器$G(x)=sign(f(x))=sign(\sum_{m=1}^M\alpha_mG_m(x))$

• 误分类样本在下一轮学习中起更大的作用。不改变所给的训练数据，而不断改变训练数据权值的分布，使得训练数据在基本分类器的学习中起不同的作用， 这是AdaBoost的一个特点
• 利用基本分类器的线性组合构建最终分类器使AdaBoost的另一特点

AdaBoost算法的训练误差分析

• AdaBoost算法最终分类器的训练误差界为 $$ \frac{1}{N}\sum\limits_{i=1}\limits^N I(G(x_i)\neq y_i)\le\frac{1}{N}\sum\limits_i\exp(-y_i f(x_i))=\prod\limits_m Z_m $$ 这个的意思就是说指数损失是0-1损失的上界，这个上界使通过递推得到的，是归一化系数的连乘

AdaBoost算法的解释

• 模型为加法模型， 损失函数为指数函数， 学习算法为前向分步算法时的二分类学习方法。根据这些条件可以推导出AdaBoost

前向分步算法

• 输入：训练数据集$T={(x_1,y_1),(x_2,y_2),...,(x_N, y_N)}, x_i \in X \sube \R^n, y_i\in {-1, 1}$， 损失函数$L(y, f(x))$; 基函数集合${b(x;\gamma)}$

• 输出：加法模型$f(x)$

• 步骤：

1. 初始化$f_0(x)=0$

2. 对$m=1,2,\cdots,M$, 极小化损失函数 $$ (\beta_m,\gamma_m)=\arg\min \limits_ {\beta,\gamma}\sum_{i=1}^NL(y_i, f_{m-1}(x_i)+\beta b(x_i;\gamma)) $$

3. 更新 $$ f_m(x)=f_{m-1}(x)+\beta _mb(x;\gamma_m) $$

4. 得到加法模型 $$ f(x)=f_M(x)=\sum_{m=1}^M\beta_m b(x;\gamma_m) $$

提升树

• 提升树是以分类树或回归树为基本分类器的提升方法，被认为是统计学习中性能最好的方法之一
• 提升方法实际采用加法模型（即基函数的线性组合）与前向分步算法

提升树模型

• 以决策树为基函数的提升方法称为提升树
• 提升树模型可以表示成决策树的加法模型 $$ f_M(x)=\sum_{m=1}^MT(x;\Theta_m) $$

提升树算法

• 针对不同问题的提升树学习算法， 其主要区别在于使用的损失函数不同：

1. 平方误差损失函数用于回归问题
2. 指数损失函数用于分类问题
3. 一般损失函数的一般决策问题

回归问题的提升树算法

• 输入：训练数据集$T={(x_1,y_1),(x_2,y_2),...,(x_N, y_N)}, x_i \in X \sube \R^n,y_i \in Y \sube R$

• 输出：提升树$f_M(x)$

• 步骤：

1. 初始化$f_0(x)=0$
2. 对$m=1,2,\dots,M$
   1. 计算残差 $$ r_{mi}=y_i-f_{m-1}(x_i), i=1,2,\dots,N $$
   2. 拟合残差$r_{mi}$学习一个回归树，得到$T(x;\Theta_m)$
   3. 更新$f_m(x)=f_{m-1}(x)+T(x;\Theta_m)$
3. 得到回归问题提升树 $$ f(x)=f_M(x)=\sum_{m=1}^MT(x;\Theta_m) $$

梯度提升(GBDT)

输入： 训练数据集$T={(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)}, x_i \in x \sube \R^n, y_i \in y \sube \R$；损失函数$L(y,f(x))$ 输出：回归树$\hat{f}(x)$ 步骤：

1. 初始化 $$ f_0(x)=\arg\min\limits_c\sum_{i=1}^NL(y_i, c) $$

2. 对$m=1,2,\cdots,M$

（ a ）对$i=1,2,\cdots,N$,计算 $$ r_{mi}=-\left[\frac{\partial L(y_i, f(x_i))}{\partial f(x_i)}\right]{f(x)=f{m-1}(x)} $$ （ b ）对$r_{mi}$拟合一个回归树，得到第$m$棵树的叶节点区域$R_{mj}, j=1,2,\dots,J$

（ c ） 对$j=1,2,\dots,J$，计算 $$ c_{mj}=\arg\min_c\sum_{xi\in R_{mj}}L(y_i,f_{m-1}(x_i)+c) $$

4. 更新 $$ f_m(x)=f_{m-1}(x)+\sum_{j=1}^Jc_{mj}I(x\in R_{mj}) $$

5. 得到回归树 $$ \hat{f}(x)=f_M(x)=\sum_{m=1}^M\sum_{j=1}^Jc_{mj}I(x\in R_{mj}) $$

习题解答

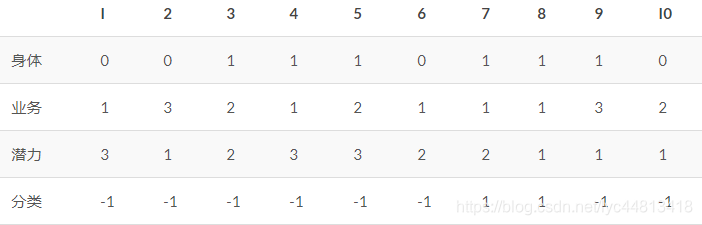
• 某公司招聘职员考查身体、业务能力、发展潜力这 3 项。身体分为合格1、不合格0两级，业务能力和发展潜力分为上1、中2、下3三级分类为合格1 、不合格-1两类。已知10个人的数据，如下表所示。假设弱分类器为决策树桩。.试用AdaBoost算法学习一个强分类器。 代码传送门

• 比较支持向量机、 AdaBoost 、逻辑斯谛回归模型的学习策略与算法。

  • 支持向量机的学习策略是当训练数据近似线性可分时，通过软间隔最大化，学习一个线性分类器，其学习算法是SMO序列最小最优化算法
  • AdaBoost的学习策略是通过极小化加法模型的指数损失，得到一个强分类器，其学习算法是前向分步算法
  • 逻辑斯谛回归模型的学习策略是在给定的训练数据条件下对模型进行极大似然估计或正则化的极大似然估计，其学习算法可以是改进的迭代尺度算法（IIS），梯度下降法，牛顿法以及拟牛顿法