| output |
|---|
html_document |
Once we have normalized the data and removed confounders we can carry out analyses that are relevant to the biological questions at hand. The exact nature of the analysis depends on the dataset. Nevertheless, there are a few aspects that are useful in a wide range of contexts and we will be discussing some of them in the next few chapters. We will start with the clustering of scRNA-seq data.
One of the most promising applications of scRNA-seq is de novo discovery and annotation of cell-types based on transcription profiles. Computationally, this is a hard problem as it amounts to unsupervised clustering. That is, we need to identify groups of cells based on the similarities of the transcriptomes without any prior knowledge of the labels. Moreover, in most situations we do not even know the number of clusters a priori. The problem is made even more challenging due to the high level of noise (both technical and biological) and the large number of dimensions (i.e. genes).
When working with large datasets, it can often be beneficial to apply some sort of dimensionality reduction method. By projecting the data onto a lower-dimensional sub-space, one is often able to significantly reduce the amount of noise. An additional benefit is that it is typically much easier to visualize the data in a 2 or 3-dimensional subspace. We have already discussed PCA (chapter @ref(visual-pca)) and t-SNE (chapter @ref(visual-pca)).
Unsupervised clustering is useful in many different applications and it has been widely studied in machine learning. Some of the most popular approaches are hierarchical clustering, k-means clustering and graph-based clustering.
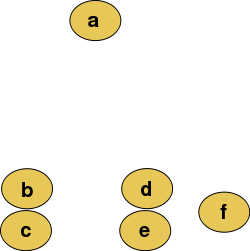
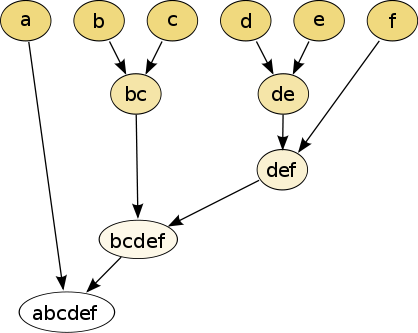
In hierarchical clustering, one can use either a bottom-up or a top-down approach. In the former case, each cell is initially assigned to its own cluster and pairs of clusters are subsequently merged to create a hieararchy:
(\#fig:clust-hierarch-raw)Raw data
(\#fig:clust-hierarch-dendr)The hierarchical clustering dendrogram
With a top-down strategy, one instead starts with all observations in one cluster and then recursively split each cluster to form a hierarchy. One of the advantages of this strategy is that the method is deterministic.
In k-means clustering, the goal is to partition N cells into k different clusters. In an iterative manner, cluster centers are assigned and each cell is assigned to its nearest cluster:
(\#fig:clust-k-means)Schematic representation of the k-means clustering
Most methods for scRNA-seq analysis includes a k-means step at some point.
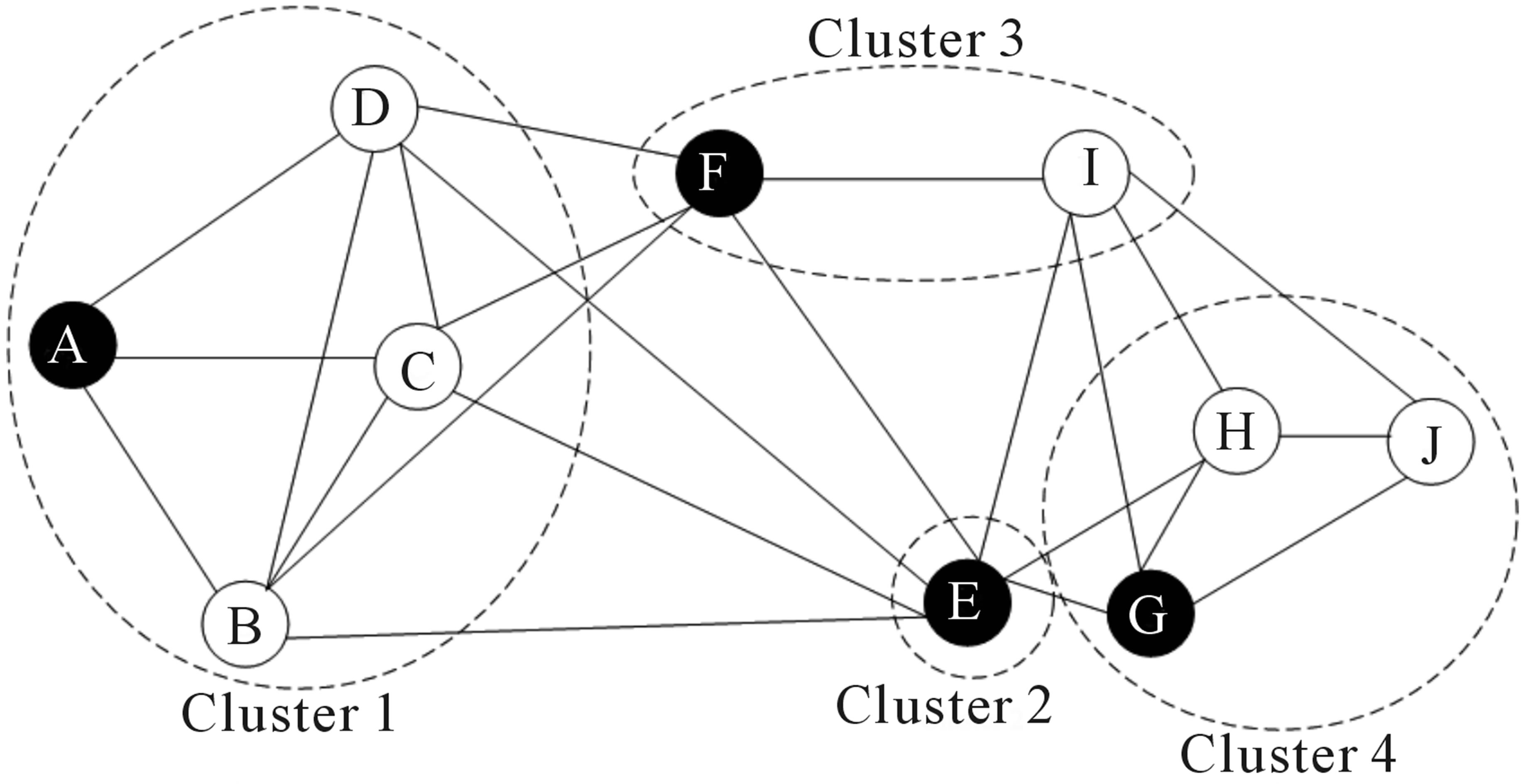
Over the last two decades there has been a lot of interest in analyzing networks in various domains. One goal is to identify groups or modules of nodes in a network.
(\#fig:clust-graph)Schematic representation of the graph network
Some of these methods can be applied to scRNA-seq data by building a graph where each node represents a cell. Note that constructing the graph and assigning weights to the edges is not trivial. One advantage of graph-based methods is that some of them are very efficient and can be applied to networks containing millions of nodes.
- What is the number of clusters k?
- What is a cell type?
- Scalability: in the last few years the number of cells in scRNA-seq experiments has grown by several orders of magnitude from ~$10^2$ to ~$10^6$
- Tools are not user-friendly
- SINCERA [@Guo2015-ok] is based on hierarchical clustering
- Data is converted to z-scores before clustering
- Identify k by finding the first singleton cluster in the hierarchy
pcaReduce [@Zurauskiene2016-kg] combines PCA, k-means and “iterative” hierarchical clustering. Starting from a large number of clusters pcaReduce iteratively merges similar clusters; after each merging event it removes the principle component explaning the least variance in the data.
(\#fig:clust-sc3)SC3 pipeline
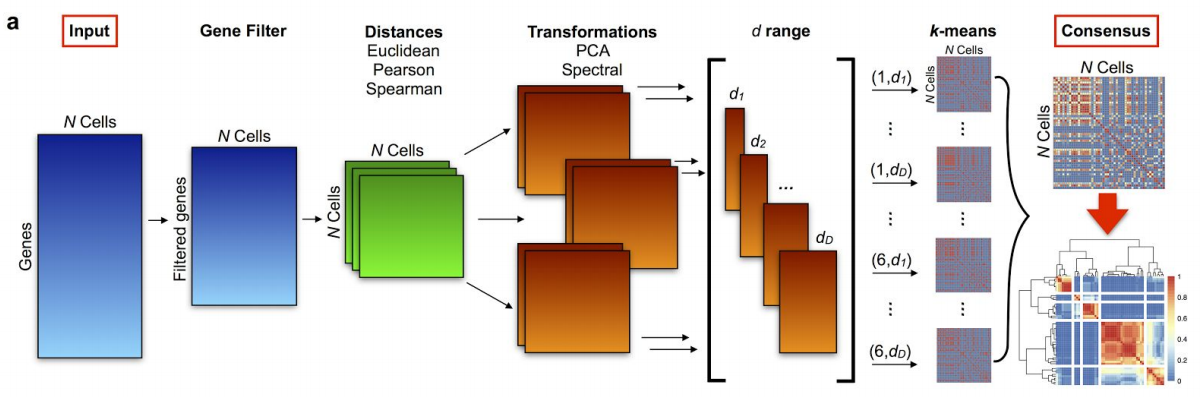
- SC3 [@Kiselev2016-bq] is based on PCA and spectral dimensionality reductions
- Utilises k-means
- Additionally performs the consensus clustering
- Based on tSNE maps
- Utilises k-means
SNN-Cliq [@Xu2015-vf] is a graph-based method. First the method identifies the k-nearest-neighbours of each cell according to the distance measure. This is used to calculate the number of Shared Nearest Neighbours (SNN) between each pair of cells. A graph is built by placing an edge between two cells If they have at least one SNN. Clusters are defined as groups of cells with many edges between them using a "clique" method. SNN-Cliq requires several parameters to be defined manually.
Seurat clustering is based on a community detection approach similar to SNN-Cliq and to one previously proposed for analyzing CyTOF data [@Levine2015-fk]. Since Seurat has become more like an all-in-one tool for scRNA-seq data analysis we dedicate a separate chapter to discuss it in more details (chapter @ref(seurat-chapter)).
To compare two sets of clustering labels we can use adjusted Rand index. The index is a measure of the similarity between two data clusterings. Values of the adjusted Rand index lie in