Trie (Prefix-Tree) is an Data-Structure used for Efficient string queries and manipulations.
It is a bit hard to build, but after building the tree, It is really helpful in solving complicated problems.
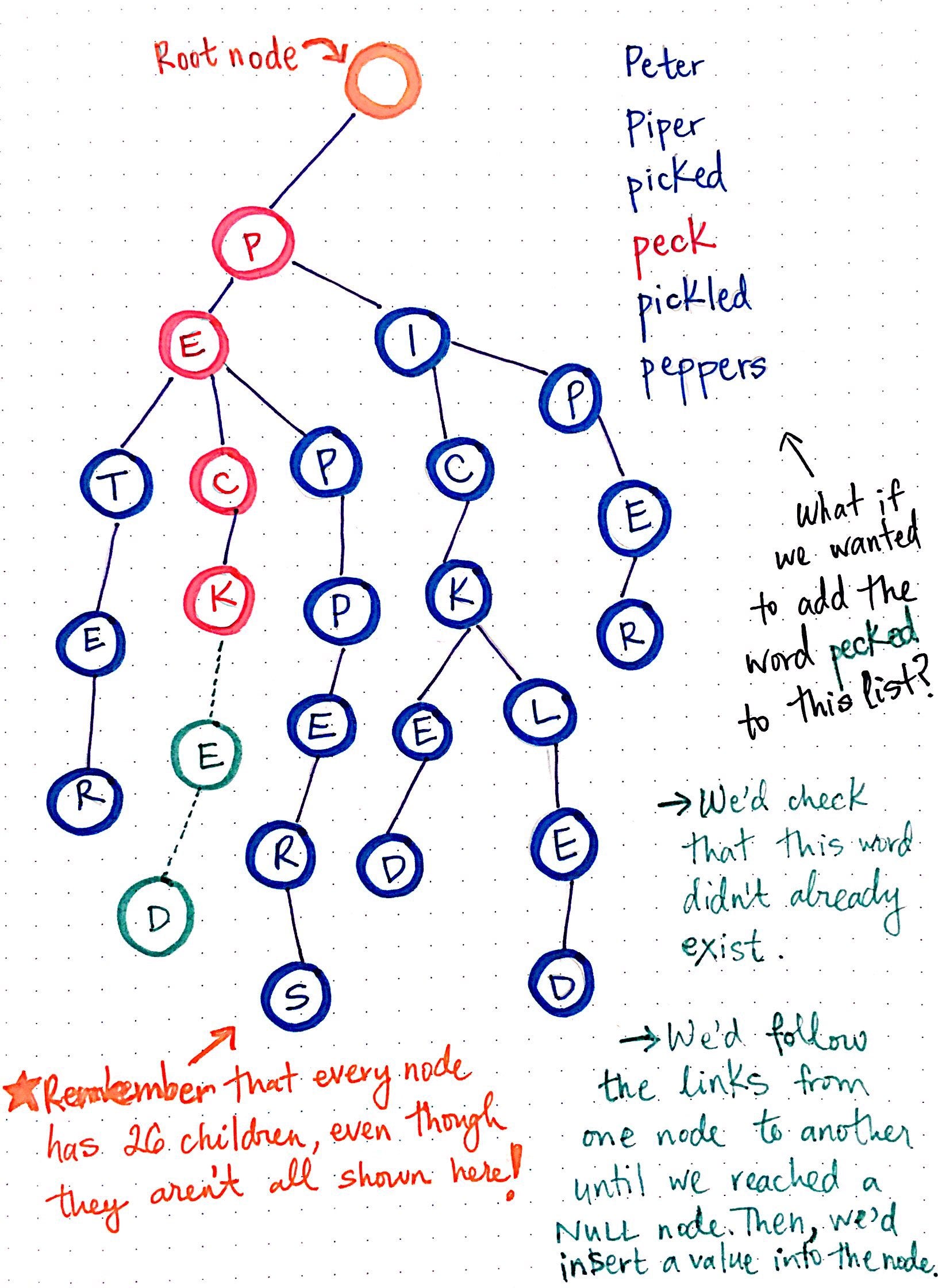
Each Node holds a character and many nodes are connected to form a string.
Each node can have upto 26 children (As there are 26 characters). Also, Each Node has an EOS flag
which indicates whether any string ends at this node or not. We can denote the character using an ASCII value.
Small English letters start from 97 and range till (97+25).
Building a tree may be divided into following steps. Lets go with the example that you want to insert "hello".
- From the root, Search for the letter 'h'. If not found, create that node and move root there.
- From the current Node, search for the letter 'e'. If not found, create that node and move root there.
- From the current Node, search for the letter 'l', If not found, create that node and move root there.
- From the current Node, search for the letter 'l', If not found, create that node and move root there.
- From the current Node, search for the letter 'o', If not found, create that node and move root there.
- As we have reached the end of string, we mark the node 'o' as EOS = true as it indicates that the string
"hello" ends here.
Similarly, when inserting any other string, we may encounter that the current node may already have that child.
In that case, just move to that node without creating any new node.
Querying is similar to Building. Keep checking if there is child node at index (say i), If there is, move there.
Else, say that the string isn't present in the tree. If you have reached the last index of string (i = n-1),
Then check for the EOS flag of the last node. If its TRUE, String is present in the tree. Else its not.
- Building a Trie: O(n*m), where n is total number of strings and m is the length(avg) of all strings combined.
- Query: O(m), where m is the length of the string being queried.
This Trie may sometimes end up being costly, there is an optimized version of Trie called as "Compressed Trie".
It compresses many letters into a single word to avoid un-necessary travel down.
